Balancer vectorberekening, voorbeelden, oefeningen

Hij Balancing Vector Het is degene die de resulterende vector contrasteert en daarom is het in staat om een ​​systeem in evenwicht te brengen, omdat het dezelfde grootte en dezelfde richting heeft, maar in tegenstelling tot dit.

Bij verschillende gelegenheden verwijst de balancerende vector naar een krachtvector. Om de evenwichtskracht te berekenen, is de resulterende kracht eerst, zoals weergegeven in de volgende figuur:

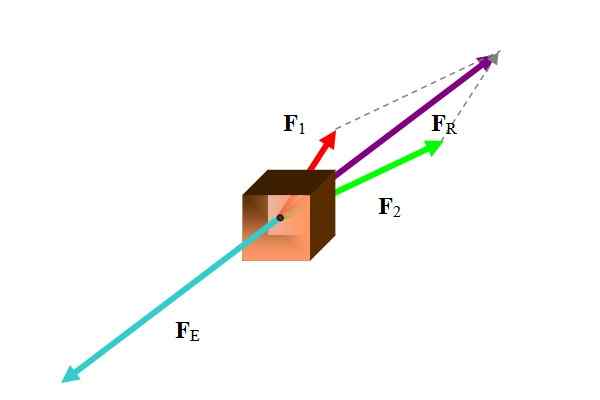
Figuur 1. Op een lichaam handelen twee krachten waarvan het resultaat is in evenwicht door geweld in turquoise kleur. Bron: zelf gemaakt.

Er zijn verschillende methoden om deze taak uit te voeren, volgens de gegevens die bij de hand zijn. Aangezien de krachten vectoren zijn, is het resultaat de vectorsom van de deelnemende krachten:

F_R = F₁ + F₂ + F₃ +  .. .

Onder de te gebruiken methoden zijn grafische methoden zoals polygonaal, parallellogram en analytische methoden zoals de ontleding van krachten in hun Cartesiaanse componenten. In het voorbeeld werd de figuur de parallellogrammethode gebruikt.

Zodra de resulterende kracht is gevonden, is de evenwichtskracht precies de tegenovergestelde vector.

Ja F_EN Het is de evenwichtskracht, dan is het dat vervuld F_EN Op een bepaald punt toegepast, garandeert het de balans van de systeemvertaling. Als het een enkel deeltje is, zal het niet bewegen (of misschien doet het het met constante snelheid), maar als het een uitgebreid object is, zal het nog steeds de mogelijkheid hebben om te draaien:

F_R + F_EN = 0

[TOC]

Voorbeelden

De evenwichtskrachten zijn aan alle kanten aanwezig. Wij zelf worden in evenwicht gebracht door de kracht die de stoel uitoefent om het gewicht te compenseren. De objecten in rust: boeken, meubels, plafondlampen en een groot aantal mechanismen worden continu in evenwicht gebracht door krachten.

Kan u van dienst zijn: Inelastische schokken: in een dimensie en voorbeelden

Een rustboek op een tafel wordt bijvoorbeeld in evenwicht gebracht door de normale kracht die het op het boek uitoefent, waardoor het valt om te vallen. Hetzelfde geldt voor de ketting of kabel die de lamp vasthoudt die aan het plafond hangt in een kamer. De kabels die een lading bevatten, worden hun gewicht verdeeld door de spanning erin.

In een vloeistof kunnen sommige objecten drijven en in rust blijven, omdat hun gewicht wordt gecompenseerd door een oplopende kracht die wordt uitgeoefend door de vloeistof, genaamd duw.

Verschillende mechanismen moeten in evenwicht zijn, wetende de balanceringskrachtvector zoals staven, balken en kolommen.

Bij het gebruik van een evenwicht is het noodzakelijk om op de een of andere manier het gewicht van het object in evenwicht te brengen met een equivalent van de kracht, ofwel het toevoegen van gewichten of door bronnen.

Krachttafel

De krachttafel wordt in het laboratorium gebruikt om de evenwichtige kracht te bepalen. Het bestaat uit een cirkelvormig platform, waarvan u het bovenaanzicht in de figuur hebt, en dat heeft een transporter om hoeken te meten.

Aan de randen van de tafel zijn er katrollen waardoor snaren die gewichten bevatten en die samenkomen in een hoepel die in het midden is.

Er zijn bijvoorbeeld twee gewichten opgehangen. De spanningen die door deze gewichten op de snaren worden gegenereerd, worden in figuur 2 rood en blauw getekend. Een derde weegt groen, kan de resulterende kracht van de andere twee in evenwicht brengen en het systeem in evenwicht houden.

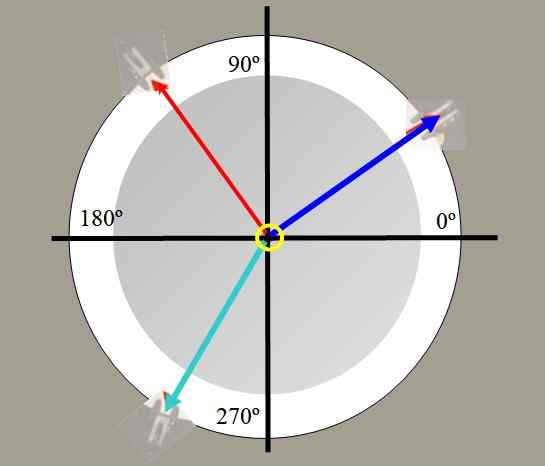Figuur 2. Bekijk vanaf de bovenkant van de krachttafel. Bron: zelf gemaakt.

Met de tabel met krachten kunt u het vectorkarakter van de krachten verifiëren, krachten ontleden, de evenwichtskracht vinden en Lamy's stelling verifiëren:

Kan u van dienst zijn: zon

Als een lichaam is in evenwicht dankzij drie coplanaire, gelijktijdige en niet -colineale (niet -parallelle) krachten, genaamd NAAR, B En C, De relatie tussen deze krachten is als volgt:

A/ sin α = b/ sen β = c/ sen γ

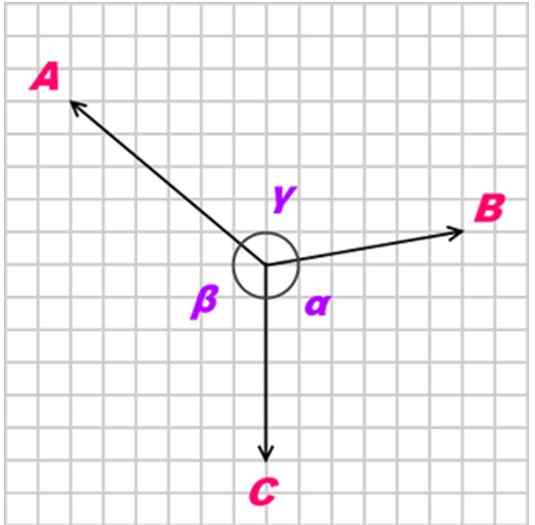figuur 3. Lamy's stelling is van toepassing op gelijktijdige en coplanaire troepen. Bron: Wikimedia Commons.

Opgeloste oefeningen

-Oefening 1

In de krachttafel in figuur 2 weegt 225 g (blauwe spanning) en 150 g (rode spanning) worden opgehangen, met de getoonde hoeken. Zoek de waarde van de evenwichtskracht en de hoek die deze vorm met de verticale as vormt.

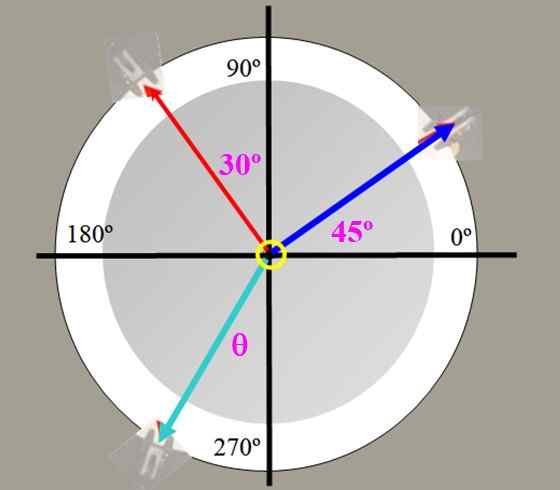Figuur 4. Krachttafel voor oefening 1.

Oplossing

Het probleem kan worden bewerkt met de gewichten uitgedrukt in gram (krachten). Laat P₁ = 150 gram en P₂ = 225 gram, de respectieve componenten van elk zijn:

P_1x = 225 . Cos 45º G = 159.10 g; P_1y = 225 . Cos 45º G = 159.10 g

P_2x = -150 . Sen 30º G = -75.00 g; P_{2 en} = 150 . Cos 30º G = 129.90 g

Het resulterende gewicht P_R De componenten voegt algebraïsch toe:

P_RX = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

Het evenwichtsgewicht P_EN is de tegenovergestelde vector P_R:

P_Ex = -84.10 g

P_Hoi = -289.00 g

De omvang van het evenwichtsgewicht wordt berekend door:

P_EN = (P_Ex² + P_Hoi²))^1/2 = ((-84.10)² + (-289.00)²))^1/2 G = 301 g

De hoek θ van de figuur is:

θ = arctg (-84.10 / -289.00) = 16.2e ten opzichte van de as En negatief.

-Oefening 2

Zoek de balancerende vector van het systeem dat in de figuur wordt getoond, wetende dat elk vierkant 10 m kant meet.

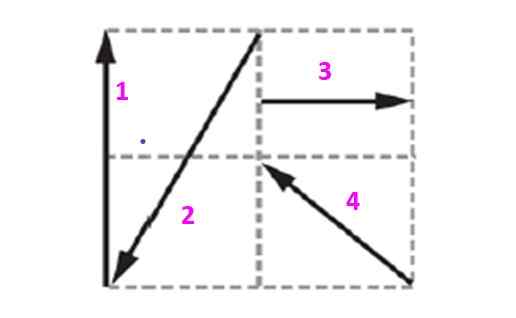Figuur 5. Diagram voor het voorbeeld opgelost 2.

Oplossing

De vectoren in dit raster zullen worden uitgedrukt in termen van de eenheid en orthogonale vectoren Je En J die het vliegtuig bepalen. Vector 1, die zal worden aangeduid als v₁ Het heeft een omvang van 20 m en is verticaal naar boven gericht. Het kan worden uitgedrukt als:

Het kan u van dienst zijn: stralingswarmteoverdracht (met voorbeelden)

v₁ = 0 Je +twintig J M

Uit de tekening wordt waargenomen dat vector 2 is:

v₂ = -10 Je - twintig J M

Vector 3 is horizontaal en punten in het positieve adres:

v₃ = 10 Je + 0 J  M

Ten slotte is vector 4 45 º hellend, omdat het de diagonaal van het vierkant is, daarom meten de componenten hetzelfde:

v₄ = -10 Je + 10 J M

Merk op dat het teken -.

De resulterende vector wordt verkregen door de componentcomponent toe te voegen:

v_R = -10 Je + 10 J M

Dan is de balancerende vector van het systeem:

v_EN = 10 Je - 10 J M

Referenties

1. Beardon, T. 2011. Een inleiding tot vectoren. Hersteld van: nrich.Wiskunde.borg.
2. Bedford, 2000. NAAR. Mechanica voor engineering: statisch. Addison Wesley. 38-52.
3. Figueroa, D. Serie: Physics for Science and Engineering. Deel 1. Kinematica.31-68.
4. Fysiek. Module 8: vectoren. Hersteld van: frtl.Utn.Edu.AR
5. Hibbeler, R. 2006. Mechanica voor ingenieurs. Statisch. 6e editie. Continentaal redactioneel bedrijf. 15-53.
6. Toevoegingscalculator vector. Hersteld van: 1728.borg
7. Vectoren. Hersteld van: Wikibooks.borg