Gratis vectoren eigenschappen, voorbeelden, oefeningen

De Gratis vectoren Zij zijn degenen die volledig worden gespecificeerd door hun omvang, hun richting en hun betekenis, zonder dat het nodig is om een ​​toepassingspunt of een bepaalde oorsprong aan te geven.

Aangezien oneindige vectoren op deze manier kunnen worden getekend, is een vrije vector geen unieke entiteit, maar een reeks parallelle en identieke vectoren die onafhankelijk zijn van de plaats waar ze zich bevinden.

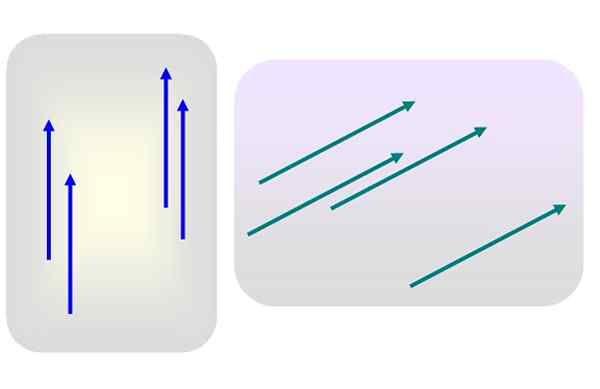
Figuur 1. Verschillende gratis vectoren. Bron: zelf gemaakt.

Laten we zeggen dat er verschillende vectoren van magnitude 3 verticaal omhoog zijn gericht, of magnitude 5 en hellend naar rechts, zoals in figuur 1.

Geen van deze vectoren wordt specifiek op een bepaald punt toegepast. Dan is een van de blauwe of groene vectoren representatief voor hun respectieve groep, omdat de kenmerken ervan - module, richting en zin - helemaal niet worden gewijzigd wanneer ze worden overgebracht naar een andere plaats van het vliegtuig.

Een vrije vector wordt meestal aangegeven in gedrukte tekst met een kleine en gewaagde letter bijvoorbeeld v. Of met kleine letters en een pijl bovenop als het een manuscripttekst is.

[TOC]

 Voorbeelden

Het voordeel dat vrije vectoren hebben, is dat ze per vliegtuig of ruimte kunnen worden verplaatst en hun eigenschappen kunnen behouden, omdat elke vertegenwoordiger van de set even geldig is.

Daarom worden in de natuurkunde en mechanica vaak gebruikt. Om bijvoorbeeld de lineaire snelheid van een vaste stof aan te geven die beweegt, is deze niet nodig om een ​​bepaald punt van het object te kiezen. Dan gedraagt ​​de snelheidsvector zich als een vrije vector.

Een ander voorbeeld van vrije vector is het paar krachten. A paar Het bestaat uit twee krachten van gelijke grootte en richting, maar uit tegengestelde zintuigen, uitgeoefend in verschillende punten van een vaste stof. Het effect van een paar is niet om het object over te dragen, maar om een ​​rotatie te veroorzaken dankzij de moment geproduceerd.

Figuur 2 toont een paar krachten die op een stuurwiel worden toegepast. Door krachten F₁ En F₂, Het koppel dat het stuur rond het midden draait, wordt gemaakt en in een schema.

Het kan u van dienst zijn: BORON NITRIDE (BN): structuur, eigenschappen, verkrijgen, gebruik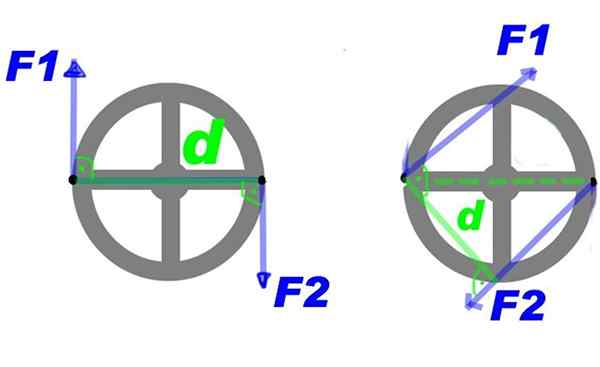 Figuur 2. Een paar krachten die op een stuurwiel worden toegepast, biedt een scorebeurt. Bron: Bensko [Public Domain].

U kunt enkele wijzigingen aanbrengen op het paar en hetzelfde roterende effect blijven verkrijgen, bijvoorbeeld verhogen de kracht, maar verminder de afstand daartussen. Of handhaven kracht en afstand, maar breng het paar aan op een andere paar punten op het stuur, dat wil zeggen, draai het koppel rond het midden.

De tijd van het paar krachten of eenvoudigweg paar, Het is een vector waarvan de module is FD en staat loodrecht op het wielvlak loodrecht. In het voorbeeld van de conventie is de Time Turn negatief logisch.

Eigenschappen en kenmerken

In tegenstelling tot de vrije vector V, de vectoren Aab En CD Ze zijn gefixeerd (zie figuur 3), omdat ze het uitgangspunt en het aankomstpunt hebben gespecificeerd. Maar apparatuur met elkaar zijn, en op zijn beurt met de vector v, Ze zijn representatief voor de vrije vector v.

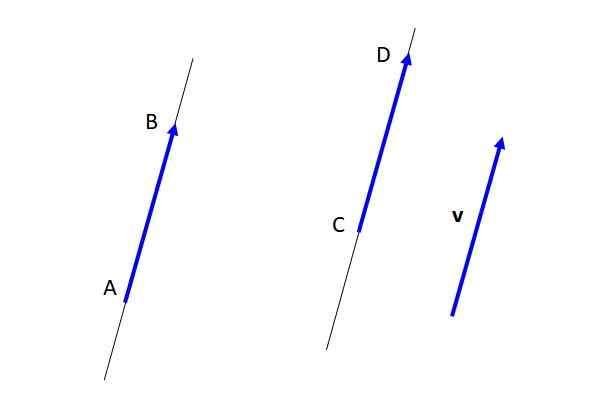figuur 3. Gratis vectoren, apparatuur en vaste vectoren. Bron: zelf gemaakt.

De belangrijkste eigenschappen van vrije vectoren zijn de volgende:

-Elke vector Aab (Zie figuur 2) Het is, zoals vermeld, representatief voor de vrije vector v.

-De module, richting en betekenis zijn hetzelfde in elke vrije vectorvertegenwoordiger. In figuur 2, de vectoren Aab En CD Ze vertegenwoordigen de vrije vector v En ze zijn apparatuur.

-Gegeven een punt P van ruimte, is het altijd mogelijk om een ​​vrije vectorvertegenwoordiger te vinden v wiens oorsprong in P zit en de vertegenwoordiger is uniek. Dit is de belangrijkste eigenschap van gratis vectoren en degene die ze zo veelzijdig maakt.

Kan u dienen: Europa (satelliet): kenmerken, compositie, baan, beweging

-Een Voyed Free Vector wordt aangeduid als 0 En het is de set van alle vectoren die geen grootte, richting en betekenis missen.

-Als de vector Aab vertegenwoordigt de vrije vector v, Dan de vector Ba vertegenwoordigt de vrije vector -v.

-Notatie zal worden gebruikt V³ Om de set van alle ruimte -vrij vectoren aan te duiden en V² Om alle gratis vectoren van het vliegtuig aan te duiden.

Opgeloste oefeningen

Met gratis vectoren kunt u de volgende bewerkingen uitvoeren:

-Toevoeging

-Aftrekking

-Vermenigvuldiging van klimmen door een vector

-Scalair product tussen twee vectoren.

-Kruis product tussen twee vectoren

-Lineaire combinatie van vectoren

En meer.

-Oefening 1

Een student is van plan om vanaf een punt aan de kust te zwemmen van de ene rivier naar de andere die precies voor de voorkant is. Om niets direct te bereiken met een snelheid van 6 km / u, in loodrechte richting, maar de stroom heeft een snelheid van 4 km / u die het omleidt.

Bereken de snelheid die voortvloeit uit de zwemmer en hoeveel wordt omgeleid door de stroom.

Oplossing

De verlengingssnelheid van de zwemmer is de vector som van zijn snelheid (met betrekking tot de rivier, verticaal getrokken) en de snelheid van de rivier (getrokken van links naar rechts), die wordt uitgevoerd zoals aangegeven in de onderstaande figuur:

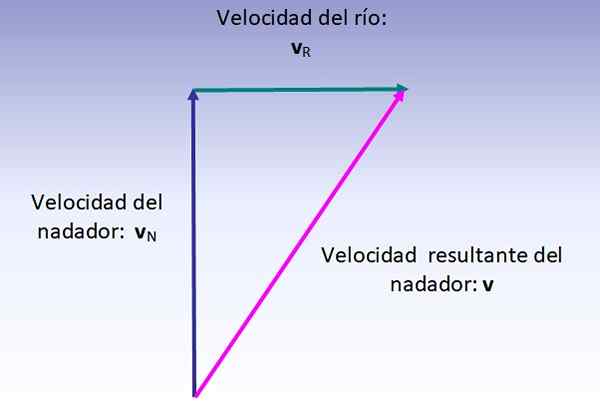
De grootte van de resulterende snelheid komt overeen met de hypotenusa van de juiste driehoek, daarom:

V = (6² + 4²)) ^½ km/h = 7.2 km/h

Het adres kan worden berekend door hoek met betrekking tot de loodrecht op de kust:

α = arctg (4/6) = 33.7e of 56.3e met betrekking tot de kust.

Oefening 2

Zoek de tijd van het paar krachten getoond in de figuur:

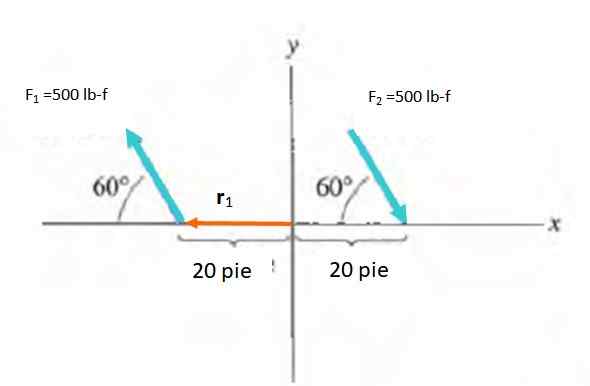
Oplossing

Het moment wordt berekend door:

Kan u van dienst zijn: Inelastische schokken: in een dimensie en voorbeelden

M = R X F

De eenheden van het moment zijn LB-F.voet. Aangezien het koppel zich in het vlak van het scherm bevindt, wordt het moment loodrecht gericht, hetzij naar buiten of naar binnen.

Aangezien het koppel van het voorbeeld de neiging heeft om het object te draaien waarop het wordt toegepast (dat niet in de figuur wordt getoond) in een schema, wordt dit moment overwogen door in het scherm te wijzen en met een negatief teken.

De omvang van het moment is m = f.D.sin a, in de hoek tussen de kracht en de vector R. U moet een punt kiezen om het moment te berekenen, wat een vrije vector is. De oorsprong van het referentiesysteem wordt daarom gekozen R gaat van O naar het punt van toepassing van elke kracht.

M₁ = M₂ = -Fdsen60º = -500 . twintig .Sen 60º lb-f . voet = -8660.3 lb-f . voet

Het netto moment is de som van m₁ en M₂: -17329.5 lb-F . voet.

Referenties

1. Beardon, T. 2011. Een inleiding tot vectoren. Hersteld van: nrich.Wiskunde.borg.
2. Bedford, 2000. NAAR. Mechanica voor engineering: statisch. Addison Wesley. 38-52.
3. Figueroa, D. Serie: Physics for Science and Engineering. Deel 1. Kinematica.31-68.
4. Fysiek. Module 8: vectoren. Hersteld van: frtl.Utn.Edu.AR
5. Hibbeler, R. 2006. Mechanica voor ingenieurs. Statisch. 6e editie. Continentaal redactioneel bedrijf. 15-53.
6. Toevoegingscalculator vector. Hersteld van: 1728.borg
7. Vectoren. Hersteld van: het is.Wikibooks.borg