Fourier Transform -eigenschappen, toepassingen, voorbeelden

De Fourier -transformatie Het is een methode voor analytische adequaatheid die is gericht op integreerbare functies die tot de familie van T behorenUitgebreide geresformeerd. Het bestaat uit een herdefinitie van functies F (t) in termen van cos (t) en sen (t).

De trigonometrische identiteiten van deze functies, samen met hun afleiding- en antididiveringskenmerken, dienen om Fourier's transformatie te definiëren door de volgende complexe functie:

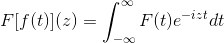
Die wordt vervuld terwijl de uitdrukking zinvol is, dat wil zeggen, wanneer de onjuiste integraal convergent is. Algebraïsch wordt gezegd dat de transformatie van Fourier een lineaire homeomorfisme is.

Elke functie die met Fourier -transformatie kan worden bewerkt, moet nietigheid buiten een gedefinieerde parameter presenteren.

[TOC]

Eigenschappen

Bron: Pexels

De Fourier -transformatie voldoet aan de volgende eigenschappen:

Bestaan

Om het bestaan ​​van de Fourier -transformatie te verifiëren in een F (t) -functie gedefinieerd in de royals R, Aan de volgende 2 axioma's moeten worden voldaan:

1. f (t) is voor alles continu in stukken R
2. f (t) is integreerbaar in R

Fourier -transformatie lineariteit

Laat m (t) en n (t) twee twee functies met gedefinieerde Fourier getransformeerd, met constanten A en B Any.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Die ook afhankelijk is van de lineariteit van de integraal van dezelfde naam.

Fourier getransformeerd van een derivaat

Je hebt een functie F  die in alle reais continu en integreerbaar is, waar:

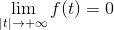
En de afgeleide van F (f ') Het is continu en gedefinieerd in stukken in alles R

De Fourier -transformatie van een derivaat wordt gedefinieerd door integratie door onderdelen, door de volgende uitdrukking:

F [f '(t)] (z) = izzF [f (t)] (z)

In hogere orde afleidingen zal het op een homologe manier worden toegepast, waar je voor alle n 1 moet:

F [F ^N'(t)] (z) = (iz)^NF [f (t)] (z)

Differentiatie van de Fourier -transformatie

Je hebt een functie F  die in alle reais continu en integreerbaar is, waar:

I (D/DZ)F [f (t)] (z) = F  [T .  f (t)] (z)

Fourier getransformeerd van een vertaling

Voor iedereen θ die tot een set behoort en T Dat is van de set s ', je moet:

F [ τ_naar θ] =  En^-IAY F [[ θ]                                 F [ τ_naarT ] =  En^-Iax  F [[ T]   

Met  τ_naar  werken als vertaaloperator op de vector aan.

Vertaling van de Fourier -transformatie

Voor iedereen θ die tot een set behoort en T Dat is van de set s ', je moet:

τ_naar F [θ] =  F [En^-Iax.θ]                                τ_naar F [t ] =  F [En^-IAY . T]

Kan u van dienst zijn: Hypercubo: Definitie, Dimensies, Coördinaten, Uitgevouwen

Voor iedereen naar die tot R

Fourier -transformatie van een schaalgroep

Voor iedereen θ die tot een set behoort s. T dat behoort tot de set s '

λ behorend bij R - 0  Je moet:

F [θ (λx)] = (1 / | λ |) F [θ] (En/λ))                 

F [T (λx)] = (1 / | λ |) F [T] (en/λ))

Ja F Het is een continue en puur integreerbare functie, waarbij a> 0. Dus:

F [f (at)] (z) =   (1/A) F [f (t)] (z/a) 

Om dit resultaat aan te tonen, kunnen we doorgaan met de verandering van variabele.

Wanneer t → + dan s = op → + ∞

Wanneer t → - dan s = op → - ∞

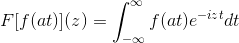
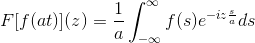
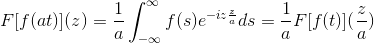
Symmetrie

Om de symmetrie van de Fourier Transforma te bestuderen.

Je hebt θ en δ die tot S. Van daaruit kan worden afgeleid dat:

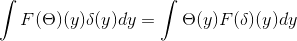
Het verkrijgen van

1 / (2π)^D  F [θ ], F [δ] Parseval -identiteit

1 / (2π)^D/2  || F [θ ] ||_L²_R^D     Plancherel -formule

Fourier transformeerde van een product in convolutie

De convolutie van functies achtervolgt soortgelijke doelstellingen die in de Laplace -transformatie verwijst naar het product onder zijn Fourier -transformaties.

Het heeft F en G als 2 functies beperkt, gedefinieerd en volledig integreerbaar:

F (f *g) = f (f) . F (g)

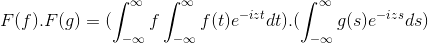
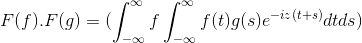
Dan bij het aanbrengen van de variabele wijziging

t + s = x; De dubbele integrale dubbele integrale wordt voortgezet

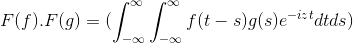
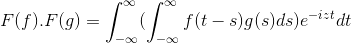
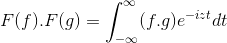
F (f) . F (g) = f (f . G)

Continuïteit en val in oneindig

Voor iedereen θ dat toebehoort R, f [ θ] gehoorzaamt de criteria van continue functie beperkt in r^D.

Ook F [ θ] (y) → 0 in c si | y | → ∞

Geschiedenis

Dit wiskundige concept werd gepresenteerd door Joseph B. Fourier in 1811 tijdens het ontwikkelen van een verdrag over de Warmte verspreid. Het werd snel overgenomen door verschillende takken van wetenschap en engineering.

Het werd vastgesteld als het belangrijkste werkinstrument in de studie van vergelijkingen met gedeeltelijke derivaten, zelfs met de werkrelatie tussen de Laplace getransformeerde en gewone differentiaalvergelijkingen.

Waar is de Fourier -transformatie voor?

Het dient voornamelijk tot significante vergelijkingen, terwijl het transformeren van uitdrukkingen die zijn afgeleid in machtselementen, die differentiële uitdrukkingen aangeven in de vorm van integreerbare polynomen.

In de optimalisatie, modulatie en modellering van resultaten fungeert het als een gestandaardiseerde uitdrukking, een frequente bron voor engineering na verschillende generaties.

Fourier's serie

Ze zijn gedefinieerde series in termen van Cosen en borsten; Ze dienen om het werk te vergemakkelijken met algemene periodieke functies. Wanneer ze worden toegepast, maken ze deel uit van de resolutietechnieken van gedeeltelijke en gewone differentiaalvergelijkingen.

Het kan u van dienst zijn: echte echte variabele functie en de grafische weergave ervan

Fourier -series zijn nog algemener dan de serie van Taylor, omdat ze periodieke discontinua -functies ontwikkelen die geen weergave hebben in Taylor -serie.

Andere vormen van de Fourier -serie

Om de Fourier -transformatie te analytisch te analyseren, is het belangrijk.

-Fourier -serie over een functie van 2l periode

Vaak is het noodzakelijk om de structuur van een Fourier-serie aan te passen aan periodieke functies waarvan de periode P = 2L> 0 is in het interval [-l, l].

-Fourier -serie in even en oneven functies

Het interval [-π, π] wordt overwogen die voordelen biedt bij het profiteren van de symmetrische kenmerken van de functies.

Als f koppel is, wordt de Fourier -serie vastgesteld als een reeks cosenos.

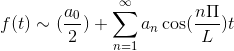
Als f vreemd is, is de Fourier -serie opgericht als een reeks borsten.

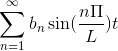
-Complexe notatie van de Fourier -serie

Als u een F (t) -functie heeft, die voldoet aan alle ontwikkelde vereisten van de Fourier-serie, is het mogelijk om deze in het interval aan te geven [-t, t] met behulp van de complexe notatie:

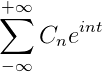
Toepassingen

Bron: Pexels

Berekening van de fundamentele oplossing

Fourier's transformatie is een krachtig hulpmiddel in de studie van gedeeltelijke differentiaalvergelijkingen van het lineaire type met constante coëfficiënten. Solliciteren voor functies met domeinen die niet gelijk worden beperkt.

Net als de Laplace -transformatie transformeert de Fourier -transformatie een functie van gedeeltelijke derivaten, in een gewone differentiaalvergelijking die veel gemakkelijker te bedienen is.

Cauchy's probleem voor de warmtevergelijking presenteert een frequent toepassingsveld van de Fourier -transformatie waar de functie wordt gegenereerd Dirichlet warmte of kernkern.

Wat betreft de berekening van de fundamentele oplossing, worden de volgende gevallen gepresenteerd waar het gebruikelijk is om de Fourier -transformatie te vinden:

-Laplace -vergelijking

-Warmtevergelijking

-Schrödinger -vergelijking

-Golfvergelijking

Signaaltheorie

De algemene reden voor de toepassing van de Fourier -transformatie in deze tak is vooral te wijten aan de karakteristieke ontleding van een signaal als een oneindige overlapping van gemakkelijker behandelbare signalen.

Het kan een geluidsgolf of een elektromagnetische golf zijn, de Fourier -transformatie drukt het uit in een eenvoudige golven overlapping. Deze weergave komt vrij vaak voor in elektrotechniek.

Kan u van dienst zijn: verticale lijn

Aan de andere kant zijn het voorbeelden van toepassing van de Fourier -transformatie in het gebied van signaaltheorie:

-Systeemidentificatieproblemen. Gevestigd f en g

-Probleem met de consistentie van het uitgangssignaal

-Problemen met het signaalfiltering

Voorbeelden

voorbeeld 1

Definieer de Fourier -transformatie voor de volgende uitdrukking:

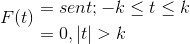
We kunnen het ook als volgt vertegenwoordigen:

F (t) = Sin (t) [h_{(T + K)} - H_{(T - k)} ]

Rechthoekige puls is gedefinieerd:

p (t) = h_{(T + K)} - H_{(T - k)}

Fourier -transformatie wordt toegepast op de volgende uitdrukking die lijkt op modulatie -stelling.

f (t) = p (t) sin (t)

Waar: F [W] = (1/2) I [P (W + 1) - P (W - 1)]

En de Fourier -transformatie wordt gedefinieerd door:

F [W] =  (1/2) I [(2/2W+1) Sen (K (W+1)) - (2/2W+1) Sen (K (W-1))]

Voorbeeld 2

Definieer de Fourier -transformatie voor expressie:

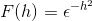Per definitie drukken we de transformatie als volgt uit

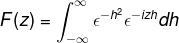
Omdat f (h) een gelijkmatige functie is, kan dat worden bevestigd

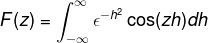In de integraal afleiden met betrekking tot Z kan de uitdrukking worden herschreven. Deze stap is belangrijk in het werk met differentiaalvergelijkingen.

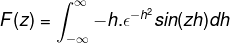
Integratie door onderdelen wordt toegepast door de variabelen en hun verschillen als volgt te selecteren

u = sin (zh) du = z cos (zh) dh

dv = h (e^-H))²                       V = (e^-H))² / 2

Het vervangen

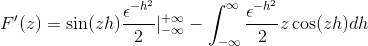
Na het evalueren onder de fundamentele stelling van de berekening

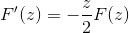
Het toepassen van eerdere kennis met betrekking tot de differentiaalvergelijkingen van de eerste orde, de uitdrukking wordt aangeduid als

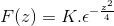
Om k te krijgen, evalueren we 

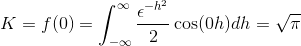
Ten slotte wordt het transformeren van Fourier gedefinieerd als

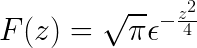
Voorgestelde oefeningen

• Bepaal de uitdrukking Fourier -transformatie
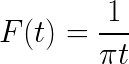
• Los de volgende onjuiste integraal op met de gelijkheid van Pareseval
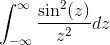
• Krijg de transformatie van de uitdrukking w/(1+w²))

Referenties

1. Duoandikoetxea zuazo, j., Fourier -analyse. Addison- Wesley IberoAmericana, Autonome University of Madrid, 1995.
2. Leeuwen, j. L., Wiskundige analyse en numerieke methoden voor wetenschap en technologie. Springer-Verlag, 1990.
3. Lieb, e. H., Gaussiaanse kernels hebben alleen Gaussiaanse maximalisers. Uitvinden. Wiskunde. 102, 179-208, 1990.
4. Dym, h., McKean, h. P., Fourier -series en integralen. Academic Press, New York, 1972.
5. Schwartz, L., Théorie des distributies. ED. Hermann, Parijs, 1966.