Isocorisch proces

Wat is een isocorisch proces?

A Isocorisch proces Het is elk thermodynamisch proces waarin het volume constant blijft. Deze processen ontvangen vaak ook de naam isometrisch of isovolumetrisch. Over het algemeen kan een thermodynamisch proces optreden bij constante druk en wordt vervolgens isobarisch genoemd.

Wanneer het bij constante temperatuur optreedt, wordt in dat geval gezegd dat het een isothermisch proces is. Als er geen warmte -uitwisseling is tussen het systeem en de omgeving, dan is er sprake van adiabatic. Aan de andere kant, wanneer er een constant volume is, wordt het gegenereerde proces isocor genoemd.

In het geval van het isocorische proces kan worden bevestigd dat in deze processen het drukwerkwerk nietig is, omdat dit het gevolg is van het vermenigvuldigen van de druk met de toename van het volume.

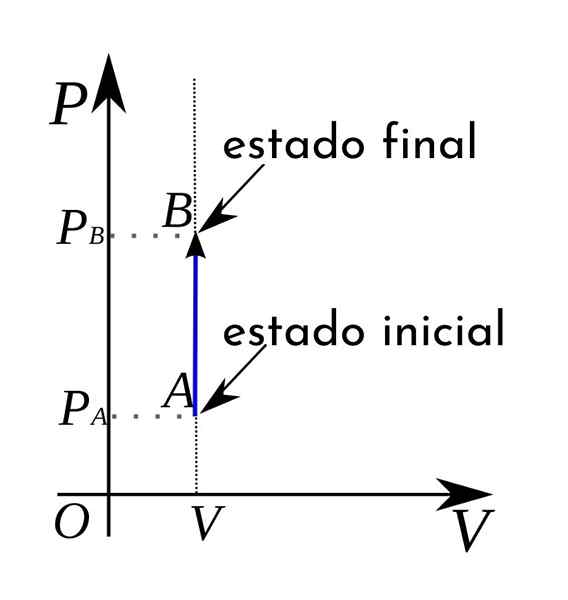
Bovendien worden in een thermodynamisch druk-volume diagram de isocorische processen weergegeven in de vorm van een verticale rechte lijn.

Formules en berekening

Het eerste principe van de thermodynamica

In de thermodynamica wordt het werk berekend op basis van de volgende uitdrukking:

W = p ∙ ∆ v

In deze uitdrukking is W het werk gemeten in joules, p de druk gemeten in Newton per vierkante meter en ∆ V is de variatie of toename van het volume gemeten in kubieke meter.

Evenzo stelt het eerste principe van thermodynamica bekend dat:

∆ u = q - w

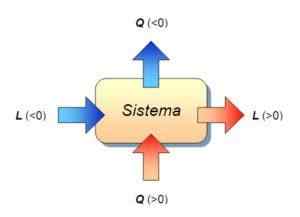
In deze formule is het het werk van het systeem of op het systeem, dat de warmte is ontvangen of uitgegeven door het systeem, en ∆ u Het is de interne energievariatie van het systeem. Bij deze gelegenheid worden de drie magnitudes gemeten in joules.

Omdat in een isocorisch proces het werk nul is, blijkt dat het wordt vervuld dat:

Kan je van dienst zijn: Neptune (planeet)

∆ u = q_V    (omdat, ∆ v = 0, en daarom w = 0)

Dat wil zeggen, de interne energievariatie van het systeem is alleen te wijten aan de uitwisseling van warmte tussen het systeem en de omgeving. In dit geval wordt de overgedragen warmte warmte genoemd tot constant volume.

Warmtecapaciteit bij constant volume

De warmtecapaciteit van een lichaam of systeem is het gevolg van het delen van de hoeveelheid energie in de vorm van warmte overgebracht naar een lichaam of een systeem in een bepaald proces en de temperatuurverandering door hetzelfde.

Wanneer het proces wordt uitgevoerd bij constant volume, wordt gesproken over warmtecapaciteit voor constant volume en wordt aangeduid met C_v (Molaire warmtecapaciteit).

Het zal in dat geval worden vervuld:

Q_v = N ∙ c_v  ∙ ∆t

In deze situatie is n het aantal mol, c_v Het is de bovengenoemde warmtecapaciteit van warmtecapaciteit tot constant volume en ∆T is de temperatuurstijging die door het lichaam of het systeem wordt ervaren.

Dagelijkse voorbeelden van isocorische processen

Het is gemakkelijk om je een isocorisch proces voor te stellen, het is alleen nodig om een ​​proces te bedenken dat zich bij constant volume voordoet; dat wil zeggen, waarin de container die het materiaal- of materiaalsysteem bevat, niet van volume verandert.

Een voorbeeld kan het geval zijn (ideaal) vergrendeld in een gesloten container waarvan het volume niet kan worden gewijzigd op geen enkele manier die warmte wordt geleverd. Stel dat het geval van een gas in een fles is vergrendeld.

Door warmte over te dragen naar gas, zoals reeds uitgelegd, zal het uiteindelijk resulteren in een toename of toename van de interne energie.

Het omgekeerde proces zou dat zijn van een gas dat is ingesloten in een container waarvan het volume niet kan worden gewijzigd. Als het gas afkoelt en warmte aan de omgeving geeft, dan zouden de gasdruk en de waarde van de interne energie van het gas afnemen worden verminderd.

Het kan u van dienst zijn: discrete variabele: kenmerken en voorbeelden

De ideale cyclus otto

De Otto -cyclus is een ideaal geval van de cyclus die wordt gebruikt door benzinemachines. Het eerste gebruik was echter in de machines die aardgas of andere brandstoffen in een gasvormige toestand gebruikten.

In elk geval is de ideale cyclus van Otto een interessant voorbeeld van het isocorische proces. Het gebeurt wanneer in een interne verbrandingsauto de verbranding van het benzine- en luchtmengsel onmiddellijk plaatsvindt.

In dat geval vindt een toename van de temperatuur en gasdruk in de cilinder plaats, waardoor het constante volume blijft.

Praktische voorbeelden

Eerste voorbeeld

Gegeven een gas (ideaal) vergrendeld in een cilinder voorzien van een zuiger, geeft aan of de volgende gevallen voorbeelden zijn van isocorische processen.

- Een 500 J werk aan gas is klaar.

In dit geval zou het geen isocorisch proces zijn, omdat het nodig is om het te comprimeren om het te comprimeren en daarom zijn volume te wijzigen.

- Het gas groeit horizontaal de zuiger.

Nogmaals, het zou geen isocorisch proces zijn, omdat gasuitbreiding een variatie in zijn volume impliceert.

- De cilinderzuiger is gefixeerd zodat gas niet kan worden verplaatst en het gas wordt gekoeld.

Bij deze gelegenheid zou het een isocorisch proces zijn, omdat er geen volumevariatie zou zijn.

Tweede voorbeeld

Bepaal de variatie van interne energie die een gas in een container zal ervaren met een volume van 10 L die wordt onderworpen aan 1 atm druk, als de temperatuur stijgt van 34 ºC tot 60 ° C in een isocorisch proces, bekend zijn specifieke warmte molaire warmte C_v = 2.5 ·R (wezen R = 8.31 J/mol · k).

Het kan u van dienst zijn: Graff Van Generator: Partijen, hoe het werkt, applicaties

Omdat het een constant volumeproces is, zal interne energievariatie alleen optreden als gevolg van de aan gas geleverde warmte. Dit wordt bepaald met de volgende formule:

Q_v = N ∙ c_v  ∙ ∆t

Om de geleverde warmte te berekenen, is het eerst nodig om de mol gas in de container te berekenen. Hiervoor is het noodzakelijk om hun toevlucht te nemen tot de vergelijking van ideale gassen:

P ∙ v = n ∙ r ∙ t

In deze vergelijking is n het aantal mol, r is r een constante waarvan de waarde 8,31 J/mol · k is, t is de temperatuur, p is de druk waartoe het gas gemeten in atmosferen wordt onderworpen en t is de gemeten temperatuur in Kelvin.

Het wordt gewist en verkregen:

n = r ∙ t/ (p ∙ v) = 0, 39 mol

Zodat:

∆ u = q_V  = N ∙ c_v  ∙ ∆t = 0,39 ∙ 2,5 ∙ 8.31 ∙ 26 = 210.65 J