Newton's First Law -formules, experimenten en oefeningen

De Newton's eerste wet, ook bekend als de Inceria Law, Het werd voor het eerst voorgesteld door Isaac Newton, fysiek, wiskundige, filosoof, theoloog, uitvinder en alchemist. Deze wet stelt het volgende vast: "Als een object niet aan enige kracht wordt onderworpen, of als de krachten die erop werken tegen elkaar worden geannuleerd, blijft het in een rechte lijn met constante snelheid bewegen."

In deze verklaring is het trefwoord om door te gaan. Als het terrein van de wet wordt vervuld, dan zal het object doorgaan met zijn beweging zoals het had. Tenzij een onevenwichtige kracht verschijnt en de staat van beweging verandert.

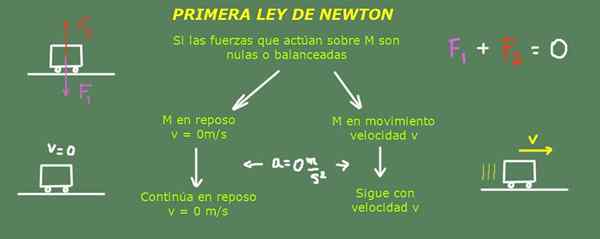
Verklaring van de eerste wet van Newton. Bron: zelf gemaakt.

Dit betekent dat als het object in rust is in rust, behalve als een kracht het uit die staat haalt. Het betekent ook dat als een object beweegt met een vaste snelheid in een rechte richting, het zo zal blijven bewegen. Zal alleen veranderen als een externe agent een kracht op hem uitoefent en zijn snelheid verandert.

[TOC]

Achtergrond van de wet

Isaac Newton werd geboren in Woolshorpe Manor (Verenigd Koninkrijk) op 4 januari 1643 en stierf in Londen in 1727.

De exacte datum waarop Sir Isaac Newton ontdekte dat zijn drie dynamische wetten niet bekend zijn met zekerheid, inclusief de eerste wet. Maar het is bekend dat het lang vóór de publicatie van het beroemde boek was Wiskundige principes van natuurlijke filosofie, 5 juli 1687.

Het woordenboek van de Royal Spaanse Academie definieert het woord traagheid als volgt:

"Eigendom van de lichamen van het handhaven van hun ruststatus of beweging als het niet is voor de actie van een kracht".

Deze term wordt ook gebruikt om te bevestigen dat elke situatie ongewijzigd blijft omdat er geen moeite is gedaan om dit te bereiken, daarom heeft het woord traagheid soms routinematige connotatie of verwaarlozing.

De pre -Newtoniaanse visie

Voorafgaand aan Newton waren de overheersende ideeën die van de Griekse Griekse filosoof Aristoteles, die beweerde dat het voor een object in gang zou blijven, het noodzakelijk is dat een kracht er op handelt. Wanneer de kracht ophoudt, zal de beweging dat ook doen. Niet zo, maar zelfs vandaag denken velen van wel.

Galileo Galilei, een briljante Italiaanse astronoom en natuurkundige die tussen 1564 en 1642 leefde, ervoer en analyseerde de beweging van de lichamen.

Een van de waarnemingen van Galileo was dat een lichaam dat op een glad en gepolijst oppervlak met een bepaalde initiële impuls glijdt, langer duurt om te stoppen en een grotere route in een rechte lijn heeft, in de mate dat de wrijving tussen het lichaam en het oppervlak lager is.

Het is duidelijk dat Galileo het idee van traagheid heeft beheerd, maar geen verklaring formuleerde die net zo nauwkeurig is als Newton.

Kan u van dienst zijn: vertaalbalans: voorwaarden, voorbeelden, oefeningen

Hier zijn enkele eenvoudige experimenten, die de lezer kan uitvoeren en de resultaten kan bevestigen. Observaties zullen ook worden geanalyseerd volgens de Aristotelische kijk op de Newtoniaanse beweging en visie.

Experimenten over traagheid

Experiment 1

Een doos wordt gepromoot op de vloer en vervolgens wordt de drijvende kracht opgehangen. We zien dat de doos op een kleine reis reist totdat deze stopt.

Laten we het vorige experiment en het resultaat ervan interpreteren, binnen het kader van de theorieën voorafgaand aan Newton en vervolgens volgens de eerste wet.

In de Aristotelische visie was de verklaring heel duidelijk: de doos stopte omdat de kracht die het bewoog, werd geschorst.

In de Newtoniaanse visie kan de doos op de vloer/vloer niet blijven bewegen met de snelheid die het had op het moment dat de kracht werd opgehangen, omdat er tussen de vloer en de doos een niet -balanceerde kracht is, waardoor de snelheid afneemt tot de Box stopt. Dit is de wrijvingskracht.

In dit experiment wordt het pand van de eerste wet van Newton niet vervuld, dus de doos stopte.

Experiment 2 

Nogmaals, het is de doos op de vloer/vloer. Bij deze gelegenheid wordt de sterkte op de doos gehandhaafd, zodat de wrijvingskracht compenseert of in evenwicht is. Dit gebeurt wanneer we de doos laten doorgaan en in een rechte richting.

Dit experiment is niet in tegenspraak met de Aristotelische visie op de beweging: de doos beweegt constant omdat een kracht erop wordt uitgeoefend.

Het is ook niet in tegenspraak met de aanpak van Newton, omdat alle krachten die op de doos handelen in evenwicht zijn. Laten we eens kijken:

• In de horizontale richting is de kracht die op de doos wordt uitgeoefend hetzelfde en van richting in strijd met de wrijvingskracht tussen de doos en de vloer.
• Dan is de netto kracht in de horizontale richting nul, daarom handhaaft de doos zijn snelheid en richting.

Ook in verticale richting zijn de krachten in evenwicht, omdat het gewicht van de doos die een kracht is die verticaal naar beneden wijst, precies wordt gecompenseerd door de contactkracht (of normaal) die de grond verticaal op de doos uitoefent.

Trouwens, het gewicht van de doos is te wijten aan de zwaartekrachtaantrekking van de aarde.

Experiment 3

We gaan door met de doos die op de vloer wordt ondersteund. In de verticale richting zijn de krachten in evenwicht, dat wil zeggen dat de netto verticale kracht nul is. Het zou zeker heel verrassend zijn als de doos omhoog ging.  Maar in horizontale richting is er wrijvingskracht.

Kan u van dienst zijn: mechanisch voordeel: formule, vergelijkingen, berekening en voorbeelden

Nu, voor het uitgangspunt van de eerste wet van Newton, moeten we de wrijving verminderen tot de minimale uitdrukking. Dit kan vrijwel ongeveer worden bereikt als we op zoek zijn naar een zeer glad oppervlak waarnaar we siliconenolie hebben gespoten.

Omdat siliconenolie de wrijving bijna tot nul vermindert, dus wanneer deze doos horizontaal is, behoudt het zijn snelheid en richting door een lang gedeelte.

Het is hetzelfde fenomeen dat optreedt met een skater op een ijsspoor, of met de ijshockeyschijf wanneer ze worden aangedreven en voor eigen rekening laten.

In de beschreven situaties, waarin het rubb.

In de Aristotelische visie kon dit niet gebeuren, omdat volgens deze naïeve theorie de beweging alleen plaatsvindt als er een netto kracht op het object in beweging is.

Het ijsoppervlak kan met zeer weinig wrijving worden overwogen. Bron: Pixabay.

Verklaring van de eerste wet van Newton

Traagheid en massa

De massa is een fysieke hoeveelheid die de hoeveelheid materie aangeeft die een lichaam of object bevat.

De massa is dan een intrinsieke eigenschap van materie. Maar materie bestaat uit atomen, die een massa hebben. De massa van het atoom is geconcentreerd in de kern. Het zijn de protonen en neutronen van de kern die praktisch de massa van het atoom en materie definiëren.

De massa wordt in het algemeen gemeten in kilogram (kg), het is de basiseenheid van het International Units System (SI).

Het prototype of de referentie van KG is een platina- en iridiumcilinder die wordt opgeslagen in het International Office of gewichten en maatregelen in Sèvres in Frankrijk, hoewel het in 2018 was gekoppeld aan de Planck Constant en de nieuwe definitie in kracht wordt vanaf 20 mei 2019.

Nou, het gebeurt dat traagheid en deeg gerelateerd zijn. Een grotere massa, grotere traagheid heeft een object. Het is veel moeilijker of duurder in termen van energie om de staat van beweging te veranderen van een massievere dan een andere minder massief.

Voorbeeld

Er is bijvoorbeeld veel meer kracht en veel meer werk nodig om een ​​doos van één ton (1000 kg) van rust te halen dan een andere kilogram (1 kg). Daarom wordt meestal gezegd dat de eerste meer traagheid heeft dan de tweede.

Vanwege de relatie tussen traagheid en massa besefte Newton dat snelheid niet representatief is voor de staat van beweging. Daarom definieerde hij een bedrag dat bekend staat als hoeveelheid beweging of momentum dat wordt aangeduid met de teksten P En het is het product van de massa M Voor snelheid v:

Het kan u van dienst zijn: GRASHOF -wet: zaken, mechanismen, voorbeelden, toepassingen

 P = M v

De vetgedrukte in de P en in de v Ze geven aan dat dit vector fysieke hoeveelheden zijn, dat wil zeggen, het zijn hoeveelheden met grootte, richting en betekenis.

In plaats daarvan de mis M Het is een scalaire hoeveelheid, die een getal is toegewezen dat groter kan zijn dan of gelijk is aan nul, maar nooit negatief. Tot het heden is een object van negatieve massa niet gevonden in het bekende universum.

Newton bracht zijn verbeelding en abstractie tot het uiterste en definieerde de oproep Gratis deeltje. Een deeltje is een materieel punt. Dat wil zeggen, het is als een wiskundig punt maar met massa:

Een vrij deeltje is dat deeltje dat zo geïsoleerd is, zo ver van een ander object in het universum dat niets wat interactie of sterkte erover kan uitoefenen.

Later definieerde Newton vervolgens de traagheidsreferentiesystemen, die zullen zijn waarin hun drie wetten worden toegepast. Hier zijn de definities volgens deze concepten:

Traagheidsreferentiesysteem

Elk coördinatensysteem gekoppeld aan een vrij deeltje, of dat wordt overgebracht met constante snelheid ten opzichte van het vrije deeltje zal een traagheidsreferentiesysteem zijn.

Newton's eerste wet (traagheidswet)

Als een deeltje vrij is, heeft het een constante hoeveelheid beweging ten opzichte van een traagheidsreferentiesysteem.

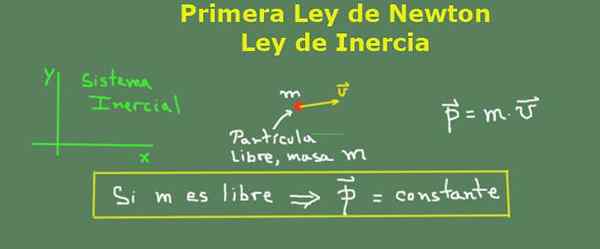Newton's eerste wet en de hoeveelheid beweging. Bron: zelf gemaakt.

Opgeloste oefeningen

Oefening 1

Een hockeyalbum is 160 gram op de ijsbaan op 3 km/u. Vind je hoeveelheid beweging.

Oplossing

De massa van het album in kilogram is: M = 0.160 kg.

De snelheid in meters boven de tweede: v = (3/3.6) m/s = 0.8333 m/s

De hoeveelheid beweging of momentum P wordt als volgt berekend: P = M*V = 0.1333 kg* m/s,

Oefening 2

Wrijving op het vorige album wordt als ongeldig beschouwd, dus het momentum wordt bewaard gebleven, terwijl niets de rechte loop van het album verandert. Het is echter bekend dat twee krachten op het album werken: het gewicht van de schijf en de contactkracht of normaal dat de vloer erop uitoefent.

Bereken de waarde van de normale kracht in Newton en de richting.

Oplossing

Omdat het momentum wordt bewaard, moet de resulterende kracht op het hockeyalbum nul zijn. Het gewicht wijst verticaal naar beneden en ok: p = m *g = 0.16 kg * 9.81 m/s²

De normale kracht moet noodzakelijkerwijs het gewicht tegengaan, dus het moet zich verticaal aanmelden en de grootte ervan zal 1 zijn.57 n.

Interessante artikelen

Newton's wetvoorbeelden in het echte leven.

Referenties

1. Alonso m., Fin e. Fysica Volume I: Mechanics. 19700000000000. Inter -American Educational Fund s.NAAR.
2. Hewitt, p. Conceptuele fysieke wetenschap. VIJFDE EDITIE. Pearson. 67-74.
3. Jong, Hugh. Universitaire natuurkunde met moderne natuurkunde. 14e ed. Pearson. 105 - 107.