Karakteristieke priemgetallen, voorbeelden, oefeningen

De priemgetallen, ook wel absolute neven genoemd, zijn die natuurlijke getallen die alleen deelbaar zijn met elkaar en 1. In deze categorie komen cijfers zoals: 2, 3, 5, 7, 11, 13, 17, 19, 23 en nog veel meer in deze categorie.

Aan de andere kant is een samengesteld nummer op zichzelf deelbaar, met 1 en ten minste nog een nummer. We hebben bijvoorbeeld op 12, die deelbaar is door 1, 2, 4, 6 en 12. Volgens het Verdrag is de 1 niet opgenomen in de lijst met priemgetallen of in de verbindingen.

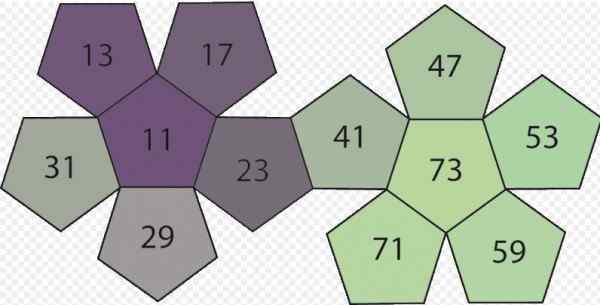
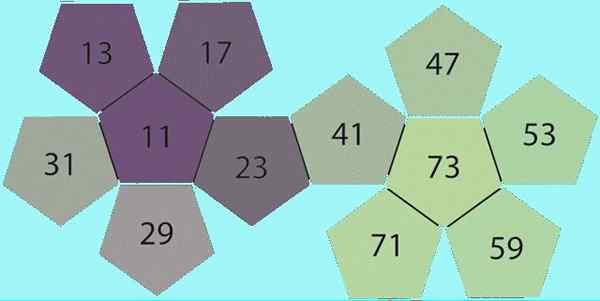Figuur 1. Enkele priemgetallen. Bron: Wikimedia Commons.

De kennis van de priemgetallen dateert uit afstandsbediening; De oude Egyptenaren hebben ze al behandeld en waren zeker al lang eerder bekend.

Deze cijfers zijn erg belangrijk, omdat elk natuurlijk getal kan worden weergegeven door het product van priemgetallen, als deze unieke weergave, behalve in de volgorde van de factoren.

Dit feit is volledig vastgesteld in een stelling genaamd De fundamentele stelling van rekenkunde, die stelt dat de cijfers die geen neven zijn, noodzakelijkerwijs zijn gemaakt van cijfersproducten die zijn.

[TOC]

Kenmerken van priemgetallen

Onder de belangrijkste kenmerken van de priemgetallen:

-Ze zijn oneindig, omdat echter een groot aantal priemgetal altijd kan worden gevonden.

-Als een priemgetal P verdeelt niet precies op een ander nummer naar, Dat wordt dan gezegd P En naar Ze zijn neven met elkaar. Wanneer dit gebeurt, is de enige gemeenschappelijke deler beide 1.

Het is niet nodig om naar Wees absolute neef. De 5 is bijvoorbeeld neef, en hoewel de 12 dat niet is, zijn beide getallen neven met elkaar, omdat de twee een gemeenschappelijke deler hebben van 1.

-Wanneer een priemgetal P Verdeel een kracht van het nummer N, Het verdeelt ook een N. Overweeg 100, wat een kracht is van 10, specifiek 10². Het gebeurt dat de 2 zowel 100 als 10 scheidt.

-Alle priemgetallen zijn oneven, behalve 2, daarom is hun laatste cijfer 1, 3, 7 of 9. De 5 is niet inbegrepen, want hoewel het oneven en neef is, is het nooit het uiteindelijke cijfer van een ander priemgetal. In feite zijn alle getallen die in 5 eindigen veelvouden hiervan en zijn daarom geen neven en nichten.

Kan u van dienst zijn: Centrale symmetrie: eigenschappen, voorbeelden en oefeningen

-Ja P Het is neef en deler van het product van twee nummers naar.B, Dus P Verdeel een van hen. Het priemgetal 3 verdeelt bijvoorbeeld het product 9 x 11 = 99, omdat 3 een deler van 9 is.

Hoe te weten of een nummer neef is

De Voornaamst Het is de naam die wordt gegeven aan de kwaliteit van zijn neef. Welnu, Franse wiskundige Fermat's kleine stelling, Dat zegt dat:

"Gegeven een natuurlijk nummer van de neef P en elk natuurlijk nummer naar Meer dan 0 is dat vervuld naar^P - naar Het is een veelvoud van P, zo lang als P Wees neef ".

We kunnen dit bijvoorbeeld bevestigen met kleine nummers, bijvoorbeeld, stel dit P = 4, dat we al weten dat het geen neef en a = 6 is:

6⁴ - 6 = 1296 - 6 = 1290

Het nummer 1290 is niet bepaald deelbaar tussen 4, daarom is 4 geen priemgetal.

Laten we de test nu doen met p = 5, wat neef is en a = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 is deelbaar tussen 5, omdat elk getal dat eindigt op 0 of 5 is. In feite 7760/5 = 1554. Aangezien Fermat's kleine stelling wordt vervuld, kunnen we ervoor zorgen dat 5 een priemgetal is.

De test door de stelling is effectief en direct met kleine cijfers, waarin de operatie gemakkelijk te uitvoeren is, maar wat we moeten doen als ze ons vragen om de primaliteit van een groot aantal te achterhalen?

In dat geval is het aantal achtereenvolgens verdeeld tussen alle kleine priemgetallen, totdat een exacte verdeling of dat het quotiënt minder is dan de deler.

Als een divisie exact is, betekent dit dat het nummer samengesteld is en als het quotiënt minder is dan de deler, betekent dit dat het nummer neef is. We zullen het in de praktijk brengen in het jaar opgelost 2.

Manieren om een ​​priemgetal te vinden

Er zijn oneindige priemgetallen en er is geen unieke formule om ze te bepalen. Het observeren van sommige priemgetallen zoals deze echter:

Kan u van dienst zijn: NULL -hoek: definitie en kenmerken, voorbeelden, oefeningen

3, 7, 31, 127 ..

Opgemerkt wordt dat ze zich in de vorm 2 bevinden^N - 1, met n = 2, 3, 5, 7, 9 ... we verzekeren u:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Maar dat kunnen we niet verzekeren^N - 1 wees neef, omdat er enkele waarden zijn van N waarvoor het niet werkt, bijvoorbeeld op 4:

2⁴ - 1 = 16 - 1 = 15

En nummer 15 is geen neef, omdat het in 5 eindigt. Een van de grootste priemgetallen die bekend zijn, gevonden door computer -gemaakte berekeningen, is echter in vorm 2^N - 1 met:

N = 57.885.161

De Mersenne -formule verzekert ons dat 2^P - 1 is altijd neef, zolang P Wees ook neef. De 31 is bijvoorbeeld neef, dus het is zeker dat 2³¹ - 1 Het is ook:

2³¹ - 1 = 2.147.483.647

Met de formule kunnen echter slechts enkele priemgetallen worden bepaald, niet alle.

Eulers formule

De volgende polynoom maakt het mogelijk om priemgetallen te vinden zolang N tussen 0 en 39 ligt:

P (n) = n² + N + 41

Later, in de sectie Oefeningen opgelost is er een voorbeeld van het gebruik ervan.

De Eratostenes -screening

Eratóstenes was een lichaamsbouw en wiskundig van het oude Griekenland die in de derde eeuw leefde.C. Hij bedacht een grafische methode om de priemgetallen te vinden die we in praktijk kunnen brengen met kleine cijfers, het wordt het Eratóstenes -scherm genoemd (een scherm is als een zeef).

-De cijfers worden in een tabel geplaatst zoals die in de animatie getoond.

-Dan zijn de gelijkmatige cijfers gelabeld, behalve de 2 waarvan we weten dat het neef is. Alle anderen zijn hiervan veelvouden en daarom zijn het geen neven en nichten.

-De veelvouden van 3, 5, 7 en 11 zijn ook gemarkeerd, exclusief ze allemaal omdat we weten dat ze neven zijn.

-De veelvouden van 4, 6, 8, 9 en 10 zijn al gemarkeerd, omdat het verbindingen zijn en daarom veelvouden van een van de aangegeven neven en nichten.

Kan u van dienst zijn: geschiedenis van trigonometrie van de oorsprong ervan

-Ten slotte zijn de resterende nummers niet gemarkeerd zijn neven en nichten.

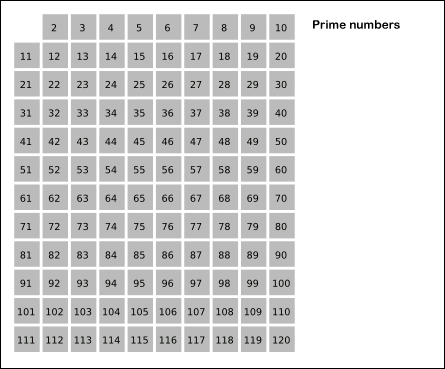Figuur 2. Eratostenes screening animatie. Bron: Wikimedia Commons.

Opdrachten

- Oefening 1

Gebruik de Euler Polynomial voor priemgetallen, zoek 3 getallen groter dan 100.

Oplossing

Dit is de polynoom die Euler voorstelde om priemgetallen te vinden, die werkt voor n waarden tussen 0 en 39.

P (n) = n² + N + 41

Via Tanteo selecteren we een waarde van n, bijvoorbeeld n = 8:

P (8) = 8² + 8 + 41 = 113

Aangezien n = 8 een priemgetal groter dan 100 produceert, evalueren we het polynoom voor n = 9 en n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Oefening 2

Ontdek of de volgende nummers neven zijn:

a) 13

b) 191

Oplossing voor

De 13 is klein genoeg om Fermat's kleine stelling en de hulp van de rekenmachine te gebruiken.

We gebruiken a = 2 zodat de cijfers niet te groot zijn, hoewel ze ook a = 3, 4 of 5 kunnen worden gebruikt:

2¹³ - 2 = 8190

8190 is deelbaar tussen 2, omdat het zelfs is, daarom is 13 neef. De lezer kan het bevestigen door dezelfde test uit te voeren met a = 3.

Oplossing B

191 is erg groot om de stelling en een gemeenschappelijke calculator te proberen, maar we kunnen de verdeling tussen elk priemgetal ertsen innemen. We laten weg om te delen door 2 omdat 191 niet eens is en de divisie niet exact is of de verhouding minder dan 2.

We hebben geprobeerd te delen door 3:

191/3 = 63,666 ..

En het geeft niet exact, noch het quotiënt is minder dan de deler (63.666 ... is groter dan 3)

We blijven 191 testen door de neven 5, 7, 11, 13 en de exacte divisie is niet bereikt, noch de verhouding minder dan de deler. Tot het tussen 17 verdeelt:

191/17 = 11, 2352 ..

Omdat het niet exact is en 11,2352 ... het is minder dan 17, het nummer 191 is neef.

Referenties

1. Baldor, een. 1986. Rekenkundig. Codex -edities en distributies.
2. Prieto, c. Primo -nummers. Opgehaald uit: pagina's.Matem.UNAM.mx.
3. Eigenschappen van priemgetallen. Hersteld van: Mae.UFL.Edu.
4. Smartick. Primo -getallen: hoe u ze kunt vinden met de zeef van Eratostenes. Hersteld van: Smartick.is.
5. Wikipedia. Priemgetal. Hersteld van: is.Wikipedia.borg.