Complexe nummers eigenschappen, voorbeelden, bewerkingen

De complexe getallen Ze zijn de numerieke set die de reële getallen en alle wortels van de polynomen bedekt, inclusief de even wortels van de negatieve getallen. Deze wortels bestaan ​​niet in de reeks reële getallen, maar in complexe getallen is de oplossing.

Een complex nummer bestaat uit een reëel deel en een ander genaamd "Imaginary". Het echte deel wordt genoemd naar, Bijvoorbeeld, en het denkbeeldige deel IB, met naar En B Echte getallen en "ik" zoals de Denkbeeldige eenheid. Op deze manier neemt het complexe nummer de vorm aan:

Z = a + ib

Figuur 1.- Binomiale weergave van een complex getal in termen van reële deel en denkbeeldig deel. Bron: Pixabay.

Voorbeelden van complexe getallen zijn 2 - 3i, -πi, 1 + (1/2) i. Maar voordat we met hen werken, laten we eens kijken waar de denkbeeldige eenheid vandaan komt Je, Gezien deze kwadratische vergelijking:

X² - 10x + 34 = 0

Waarin a = 1, b = -10 en c = 34.

Wanneer de oplosmiddelformule wordt toegepast om de oplossing te bepalen, vinden we het volgende:

Hoe de waarde van √-36 te bepalen? Er is geen reëel getal dat vierkant een negatief bedrag is. Dan wordt geconcludeerd dat deze vergelijking geen echte oplossingen heeft.

We kunnen dit echter schrijven:

√-36 = √-6² = √6² (-1) = 6√-1

Als we een bepaalde waarde definiëren X zoals dat:

X² = -1

Dus:

x = ± √-1

En de vorige vergelijking zou een oplossing hebben. Daarom werd de denkbeeldige eenheid gedefinieerd als:

I = √-1

En dus:

√-36 = 6i

Veel antiquite-wiskundigen werkten aan het oplossen van soortgelijke problemen, met de aandacht van de Renaissance Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) en Raffaele Bombelli (1526-1572).

Jaren later noemde René Descartes (1596-1650) "Imaginary" naar hoeveelheden zoals de √-36 van het voorbeeld. Om deze reden staat de √-1 bekend als de Denkbeeldige eenheid.

[TOC]

Complexe nummers eigenschappen

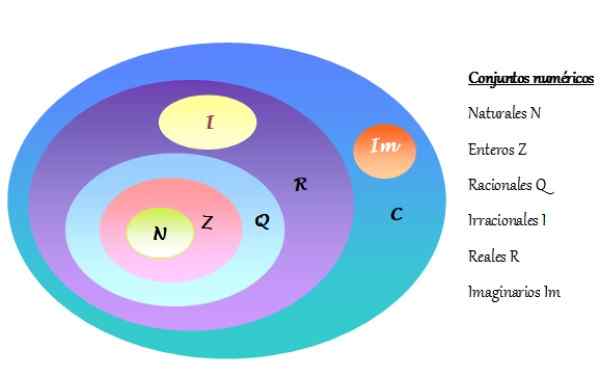
-De set van complexe getallen wordt aangeduid als C en bevat reële getallen R en denkbeeldige nummers IM. Numerieke sets worden weergegeven in een Venn -diagram, zoals weergegeven in de volgende figuur:

Kan u van dienst zijn: opgeloste factorisatieoefeningen Figuur 2. Venn -diagram van numerieke sets. Bron: f. Zapata.

-Elk complex nummer bestaat uit een echt deel en een ander denkbeeldig deel.

-Wanneer het denkbeeldige deel van een complex getal 0 is, is het een puur reëel getal.

-Als het echte deel van een complex getal 0 is, dan is het nummer puur denkbeeldig.

-Twee complexe cijfers zijn hetzelfde als hun respectieve reële deel en denkbeeldige deel hetzelfde zijn.

-Met de complexe getallen worden de bekende bewerkingen van bedragen, aftrekking, vermenigvuldiging, product en empowerment uitgevoerd, wat resulteert in een ander complex nummer.

Weergave van complexe getallen

Complexe getallen kunnen op verschillende manieren worden weergegeven. Hier zijn de belangrijkste:

- Binomische vorm

Het is de gegeven vorm in het begin, waar Z is het complexe nummer, naar is het echte deel, B is het denkbeeldige deel en Je Het is de denkbeeldige eenheid:

Z = a + ib

Of ook:

Z = x + iy

Een manier om het complexe getal te grafieken is door het complexe vlak dat in deze figuur wordt getoond. De denkbeeldige as is verticaal, terwijl de echte as horizontaal is en aangeeft als Re.

Het complexe nummer Z Het wordt in dit vlak weergegeven als een coördinaatpunt (X, y) of (A, b), Zoals wordt gedaan met de punten van het echte vliegtuig.

De afstand van de oorsprong tot punt z is de module van het complexe nummer, aangeduid als R, terwijl φ de hoek is die zich vormt R Met de echte as.

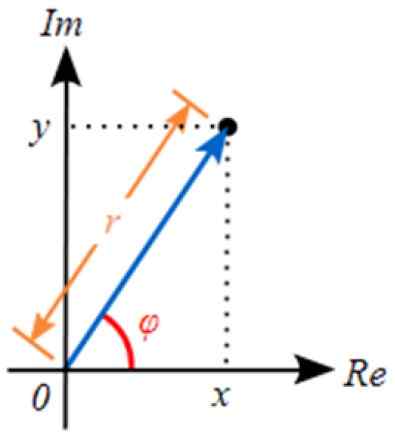
figuur 3. Weergave van een complex getal in het complexe vlak. Bron: Wikimedia Commons.

Deze weergave is nauw verwant aan die van vectoren in het echte vlak. De waarde van r komt overeen met module van het complexe nummer.

Het kan u van dienst zijn: Gauss-Seidel-methode: uitleg, toepassingen, voorbeelden

- Polaire vorm

De polaire vorm bestaat uit het uitdrukken van het complexe nummer dat de waarden van R en van φ. Als we naar de figuur kijken, de waarde van R Het komt overeen met de hypotenusa van een rechter driehoek. De categorieën zijn waard naar En B, O goed X En En.

In de binomiale of binomiale vorm kunnen we doorgaan naar de polaire vorm door:

R = √x²+En²

De engel φ Het is degene die het R -segment vormt met de horizontale as of denkbeeldige as. Het is bekend als argument van het complexe nummer. Op deze manier:

φ = arctg (y/x)

Het argument heeft oneindige waarden, rekening houdend met dat elke keer dat een rendement wordt gedraaid, wat 2π radianen waard is, R opnieuw dezelfde positie inneemt. Op deze manier wordt in het algemeen het argument van Z, aangeduid als arg (z), als volgt uitgedrukt:

Arg (z) = φ + 2kπ

Waar K heel is en dient om de hoeveelheid bochten aan te geven: 2, 3, 4 .. . Het teken geeft de betekenis van de rotatie aan, als tijd of antihorario wordt gemaakt.

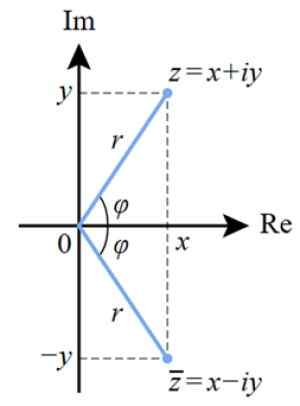
Figuur 4. Polaire weergave van een complex getal in het complexe vlak. Bron: Wikimedia Commons.

En als we de polaire vorm aan de binomiale vorm willen doorgeven, gebruiken we trigonometrische redenen. Uit de vorige figuur kunnen we dat zien:

x = r cos φ

y = r sen φ

Op deze manier z = r (cos φ+i sin φ)

Dat is zo afgekort:

z = r cis φ

Voorbeelden van complexe getallen

De volgende complexe cijfers worden binomiaal gegeven:

a) 3 + i

B) 4

d) -6i

En deze in een geordend koppel:

a) (-5, -3)

b) (0, 9)

c) (7.0)

Ten slotte krijgt deze groep polair of trigonometrisch:

a) √2 cis 45º

b) √3 cis 30º

Kan u van dienst zijn: Hypergeometrische verdeling: formules, vergelijkingen, model

c) 2 cis 315º

Waar zijn die voor?

Het nut van complexe getallen gaat verder dan de resolutie van de tweede graad vergelijking die in het begin wordt getoond, omdat ze essentieel zijn op het gebied van engineering en fysica, vooral in:

-De studie van elektromagnetische golven

-Alternatieve stroom- en spanningsanalyse

-De modellering van allerlei signalen

-Relativiteitstheorie, waarbij tijd wordt aangenomen als een denkbeeldige omvang.

Bewerkingen met complexe nummers

Met de complexe nummers kunnen we alle bewerkingen uitvoeren die met het echte worden gedaan. Sommige zijn gemakkelijker te doen als de getallen binomisch komen, zoals som en aftrekking. Aan de andere kant zijn vermenigvuldiging en verdeling eenvoudiger als ze worden uitgevoerd met de polaire vorm.

Laten we eens kijken naar enkele voorbeelden:

- voorbeeld 1

Voeg z toe₁ = 2 + 5i en z₂ = -3 -8i

Oplossing

De echte delen worden afzonderlijk toegevoegd van de denkbeeldige delen:

Z₁ + Z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Voorbeeld 2

Vermenigvuldig Z₁ = 4 cis 45º en z₂ = 5 cis 120º

Oplossing

Het kan worden aangetoond dat het product van twee complexe getallen in polaire of trigonometrisch wordt gegeven door:

Z₁ . Z₂ = r₁.R₂ Cis (φ₁ + φ₂))

Volgens dit:

Z₁ . Z₂ = (4 × 5) cis (45 + 120) = 20 cis 165º

Sollicitatie

Een eenvoudige toepassing van complexe getallen is om alle wortels van een polynoomvergelijking te vinden, zoals die aan het begin van het artikel.

In het geval van vergelijking x² - 10x + 34 = 0, bij het toepassen van de oplosmiddelformule wordt deze verkregen:

Daarom zijn de oplossingen:

X₁ = 5 + 3i

X₂ = 5 - 3i

Referenties

1. Earl, r. Complexe getallen. Hersteld van: wiskunde.os.AC.Uk.
2. Figuera, j. 20000000000000000000. Wiskunde 1e. Diversifieerd. Co-bo edities.
3. Hoffmann, J. 2005. Selectie van wiskundeproblemen. Monfort Publications.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Complexe getallen. Opgehaald uit: in.Wikipedia.borg