Lagrange interpolatie

Wat is de interpolatie van LaGrange?

De interpolatie van LaGrange is een numerieke methode voor benadering van functies, die gebruik maakt van een polynoom die bepaalde bekende punten van de functie passeert die bedoeld is om te benaderen.

Als de geschatte functie zacht is, zelfs buiten de gegeven of bekende waarden, neemt polynoom waarden in de buurt van die van de functie van interesse, vooral als deze waarden tussen de gegeven punten liggen. Daarom wordt polynoom beschouwd als een goede benadering van de functie.

Figuur 1.- Formule om Lagrange -polynomen te bouwen. Bron: f. Zapata.

Stel nu dat u een functie wilt benaderen F (x) waarvan alleen hun waarden in sommigen bekend zijn X-_Je-, met Je van 0 tot N-1. Dat wil zeggen, ze kennen elkaar N punten (X-_Je, En_Je)) met En_Je = F (x_Je)), Waar de index Je Gaat van 0 tot N-1.

In de lagrange -interpolatiemethode benadert het polynoom dat de functie nadert F (x) Het is een polynoom P (x) van graad N-1, gebouwd door de lineaire combinatie van N Polynomen L_Je(X) van graad N-1. Dit zijn de Lagrange polynomen, die als volgt worden uitgedrukt:

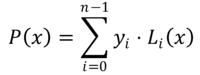
De waarden van En_Je Ze vertegenwoordigen de ordinaten die overeenkomen met de abscis X_Je Waar de functie F (x) Het is bekend, dat wil zeggen: En_Je = F (x_Je)).

Lagrange polynomen

Door lineaire combinaties tussen hen, fungeren LaGrange -polynomen als basis voor het bouwen van polynoom N -1 die zal dienen om de N Bekende punten.

De notatie voor polynomen is L_Je(x), met index I in het bereik van 0 tot n-1. De formule om Lagrange -polynomen op te stellen is als volgt:

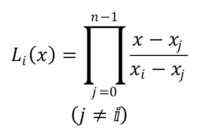
Het getoonde symbool geeft aan dat het product van n -1 monomials moet worden uitgevoerd, beginnend bij de polynoom j = 0.

Kenmerken van Lagrange -polynomen

1.- LaGrange -polynomen zijn exact hetzelfde als de eenheid wanneer geëvalueerd in de abscissa die overeenkomt met hun index, dat wil zeggen:

L_Je(X_Je) = 1

2.- Ze worden geannuleerd in de abscis van de interpolatiepunten met index die verschilt van die van dezelfde polynoom:

Kan u van dienst zijn: beschrijvende statistieken: geschiedenis, kenmerken, voorbeelden, concepten

L_Je(X_J) = 0, met i ≠ j.

3.- Het nemen van andere absciswaarden verschillend van interpolatiepunten, lagrange polynomen verwerven waarden tussen -1 en +1.

4.- Om LaGrange -polynomen te verkrijgen, is het alleen nodig om de abscis van de punten te kennen om te interpoch.

Tweede -graden Lagrange polynomen

Tweede -graden Lagrange -polynomen zijn die die het meest worden gebruikt wanneer u een interpolatie met drie punten wilt doen.

Stel dat de interpolaire functie bekend is in drie punten, die zijn:

(X₀,En₀)); (X₁, En₁)); (X₂, En₂))

Dan uw overeenkomstige Lagrange -polynomen L₀, L₁ En L₂ Ze worden zo:

L₀(x) = [(x - x₁) / (X₀ - X₁)] [(x - x₂) / (X₀ - X₂)]

L₁(x) = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)]

L₂(x) = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)]

het zou genoteerd moeten worden dat L₀(X₀) = L₁(X₁) = L₂(X₂) = 1, terwijl L_Je(X_J) = 0 zo lang als Je≠ j.

Interpolatie polynoom van tweede graad

Het is belangrijk op te merken dat in de interpolatiepolynoom van Lagrange de ordinaten van interpolatiepunten LaGrange -polynoomfactoren zijn.

Op deze manier dienen ze, zodra de polynomen zijn verkregen voor bepaalde waarden van de abscis.

In het geval van een interpolatie van de tweede klas:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

En p (x) nadert de functie f (x) in de interval (X₀, X₂)).

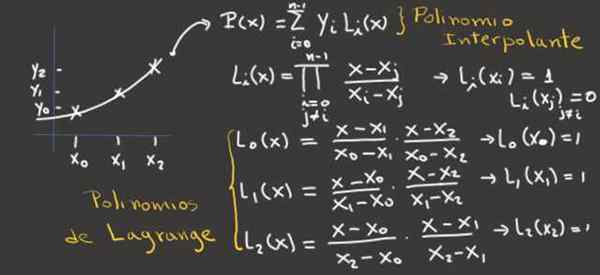Figuur 2.- Deze afbeelding laat zien hoe de LaGrange -polynomen te verkrijgen voor drie interpolatiepunten en daarvan, de interpoling polynoom. Bron: f. Zapata.

Voorbeelden

voorbeeld 1

Zoek de Lagrange -polynomen die overeenkomen met drie abscispunten X₀= 0, X₁= 1 En X₂= 2.

Zoals te zien in de vorige sectie, zullen deze polynomen zijn:

Kan u van dienst zijn: overjectieffunctie: definitie, eigenschappen, voorbeelden

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( X² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - X)

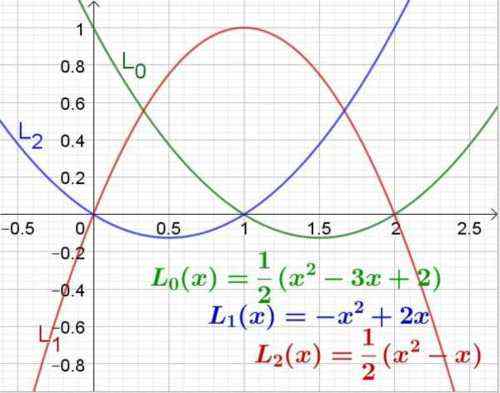figuur 3. Lagrange polynomen voor abscis -waarden 0, 1 en 2. Bron: f. Zapata.

Voorbeeld 2

U wilt de functie benaderen f (x) = arcan (x) In de interval [0, 2]. Van deze functie is alleen hun waarden bekend X₀= 0, X₁= 1 En X₂= 2, die respectievelijk zijn En₀= 0, En₁= π/4 = 0.785 En En₂= 1,107.

Daarom moet je de interpoling polynoom vinden P (x) naderend F (x) In het aangegeven interval.

In Voorbeeld 1 zijn Lagrange -polynomen al bepaald voor de absciswaarden die in deze verklaring zijn aangegeven, dus het is niet nodig om de berekening te herhalen. Interpoling Polynomial zal nu zijn:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

Die gelijkwaardig is aan:

P (x) = y₀ L₀(x) + en₁ L₁(x) + en₂ L₂(X)

In dit specifieke geval is het:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0.785 ∙ (- x² + 2x) + 1.107 ∙ (½) (x² - X)

Het bovenstaande is vereenvoudigd om:

P (x) = 0,785 ∙ (- x² + 2x) + 1.107 ∙ (½) (x² - X)

En eindelijk blijft:

P (x) = -0,2315 ∙ x² + 1.0165 ∙ x

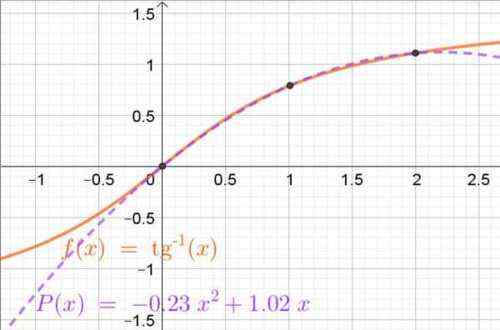Figuur 4. Interpoling polynoom verkregen door lagrange polynomen die de boog-tangente functie in het interval benadert (0, 2). Interpolatiepunten worden ook getoond. Bron: f. Zapata.

Opdrachten

Oefening 1

Verkrijg voldoende Lagrange -polynomen om een ​​benadering van de functie te hebben:

f (x) = sin (x)

In het interval [0, π] en met vijf interpolatiepunten.

Oplossing

In de eerste plaats worden de abscis van de interpolatiepunten bepaald, die gelijk worden gekozen en inclusief de uiteinden van het benaderingsinterval. Hiermee heb je:

X₀= 0; X₁= π/4; X₂= π/2; X₃= 3 π/4; X₄= π.

Kan u van dienst zijn: ongelijkheid van de driehoek: demonstratie, voorbeelden, opgeloste oefeningen

Aangezien F (x) op de extreme punten wordt geannuleerd, is het niet nodig om de LaGrange L -polynomen L te verkrijgen₀ en ik₄.

Polynomen L₁, L₂ en ik₃ Zijn:

L₁ = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)] [(x - x₃) / (X₁ - X₃)] [(x - x₄) / (X₁ - X₄)]

L₂ = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)] [(x - x₃) / (X₂ - X₃)] [(x - x₄) / (X₂ - X₄)]

L₃ = [(x - x₀) / (X₃ - X₀)] [(x - x₁) / (X₃ - X₁)] [(x - x₂) / (X₃ - X₂)] [(x - x₄) / (X₃ - X₄)]

Nu vervangen we de waarde van de abscis:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]]

Noemers zijn opgelost:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

Het is vereenvoudigd en hergroepeerd om te verkrijgen:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Oefening 2

Verkrijg de interpolatiepolynoom die de Sen (X) -functie nadert in het interval [0, π] met de vijf interpolatiepunten gekozen in Oefening 1 en hun respectieve Lagrange -polynomen.

Oplossing

De interpolatiepolynoom is:

P (x) = sin (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * L4

Het evalueren van de sinus- en vermenigvuldigingsfunctie is:

P (x) = (√2/2) l₁ + 1 * l₂ + (-√2/2) l₃

Na een moeizaam algebraïsch werk is interpolatiepolynoom:

P (x) = 2. 7481 x⁴ -vijftien. 138 x³ +23. 467 x² - 9. 5236 x

Referenties

1. Goodman, een. L. H. 1996. Algebra en trigonometrie met analytische geometrie. Pearson Education.
2. Harpe, p. D. (2000). Onderwerpen in de geometrische groepstheorie. Universiteit van Chicago Press.
3. Hazewinkel, m. (2001). Lineaire interpolatie ", Encyclopedia of Mathematics.
4. Hoffmann, E. (2002). Tot chronologie van interpolatie: van oude astronomie tot modern signaal- en beeldverwerking. Proceedings of the IEEE.
5. Wikipedia. Lagrange polynoom interpolatie. Hersteld van: Wikipedia.com