Destructieve interferentieformule en vergelijkingen, voorbeelden, oefening

De destructieve interferentie, In de natuurkunde treedt het op wanneer twee onafhankelijke golven die in hetzelfde ruimtegebied combineren, verouderd zijn. Dan komen de ruggen van een van de golven aan de valleien van de andere en het resultaat is een golf met een nulamplitude.

Verschillende golven passeren zonder probleem door hetzelfde punt in de ruimte en vervolgens volgt elk zijn pad zonder te worden beïnvloed, zoals de golven in het water van de volgende figuur:

Figuur 1. Regendruppels produceren golven op het wateroppervlak. Wanneer de resulterende golven nul breedte hebben, wordt gezegd dat interferentie destructief is. Bron: Pixabay.

Stel dat twee golven van gelijke amplitude en frequentie ω, die we zullen noemen en₁ en en₂, dat kan wiskundig worden beschreven door vergelijkingen:

En₁= Een sen (kx -Ω)

En₂ = Een sen (kx -ωt + φ)

De tweede golf en₂ Het heeft een opening φ ten opzichte van de eerste. Indien gecombineerd, omdat golven zonder problemen kunnen worden gesuperponeerd, geven ze aanleiding tot een resulterende golf die wordt genoemd en_R:

En_R = Y₁ + En₂ = Een sen (kx -ω) + a sin (kx -ωt + φ)

Door trigonometrische identiteit:

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

De vergelijking voor en_R Het transformeert in:

En_R = [2a cos (φ/2)] sin (kx - ωt + φ/2)

Nu heeft deze nieuwe golf een resulterende amplitude_R = 2a cos (φ/2), die afhankelijk is van het faseverschil. Wanneer dit faseverschil de waarden+π of -π verwerft, is de resulterende amplitude:

NAAR_R = 2a cos (± π/2) = 0

Sinds cos (± π/2) = 0. Precies dan is het wanneer de destructieve interferentie tussen golven optreedt. In het algemeen, als het argument van de cosinus van de vorm ± kπ/2 is met oneven k, de amplitude tot_R  Het is 0.

[TOC]

Destructieve interferentie voorbeelden

Zoals we hebben gezien, wanneer twee of meer golven tegelijkertijd doorgaan door een punt, overlappen ze zich, wat aanleiding geeft tot een resulterende golf waarvan de amplitude afhangt van het faseverschil tussen de deelnemers.

Kan u van dienst zijn: lineaire variatie: concept, voorbeelden, oefening opgelost

De resulterende golf heeft hetzelfde frequentie- en golfnummer als de originele golven. In de volgende animatie worden twee golven gesuperponeerd in blauwe en groene kleuren. De resulterende golf is rood.

De amplitude groeit wanneer de interferentie constructief is, maar deze wordt geannuleerd wanneer deze destructief is.

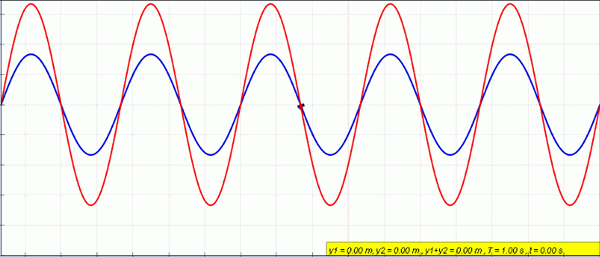Figuur 2. Blauwe en groen gekleurde golven overlappen elkaar om aanleiding te geven tot de rode golf. Bron: Wikimedia Commons.

De golven met dezelfde amplitude en frequentie worden genoemd coherente golven, Zolang ze tussen hen hetzelfde faseverschil houden φ φ. Een coherent golf voorbeeld is laserlicht.

Voorwaarde voor destructieve interferentie

Wanneer de blauwe en groene golven op een bepaald punt verouderd zijn in 180 º (zie figuur 2), betekent dit dat ze, terwijl ze bewegen, hebben Faseverschillen φ van π radianen, 3π radialen, 5π radialen enzovoort.

Op deze manier is, door het argument van de resulterende amplitude door 2 te delen, (π/2) radialen, (3π/2) radialen ... en de cosinus van dergelijke hoeken is altijd 0. Daarom is de interferentie destructief en wordt de amplitude gemaakt 0.

Destructieve golfinterferentie in water

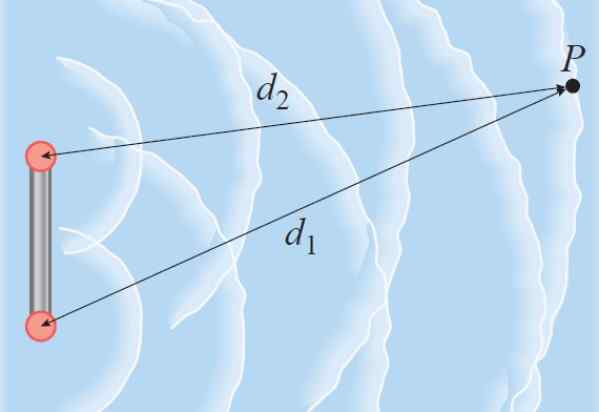
Stel dat twee coherente golven met elkaar in één beginnen. Dergelijke golven kunnen die zijn die zich door het water verspreiden dankzij twee bars die trillen. Als de twee golven naar hetzelfde punt P reizen, op verschillende afstanden touren, is het faseverschil evenredig met het padverschil.

figuur 3. De golven geproduceerd door de twee bronnen reizen in het water tot het punt P. Bron: Giambattista, een. Natuurkunde.

Als een golflengte λ is gelijk aan een verschil van 2π radialen, dan is het waar dat:

│d₁ - D₂│ / λ = faseverschil / 2π radialen

Faseverschil = 2π x│d₁ - D₂│/ λ

Kan u van dienst zijn: polarisatie van licht: typen, voorbeelden, toepassingen

Als het pad van wegen een oneven aantal golf semi-golf is, dat wil zeggen: λ/2, 3λ/2, 5λ/2 enzovoort, dan is de interferentie destructief.

Maar als het wegverschil een koppelnummer van golflengten is, is de interferentie constructief en worden de amplitudes toegevoegd op punt P.

Destructieve interferentie van lichtgolven

Lichtgolven kunnen elkaar ook verstoren, zoals Thomas Young in 1801 vermeld door hun gevierde dubbele spleetexperiment.

Young gaf licht door een spleet gemaakt op een ondoorzichtig scherm, dat volgens het Huygens -principe op zijn beurt twee secundaire lichtbronnen genereert. Deze bronnen bleven op weg door een tweede ondoorzichtig scherm met twee spleten en het resulterende licht werd op een muur geprojecteerd.

Het diagram wordt waargenomen in de volgende afbeelding:

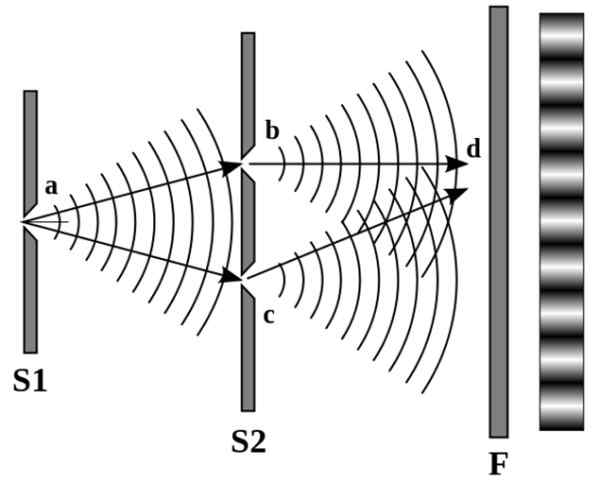Figuur 4. Het patroon van lichte en donkere lijnen aan de rechterwand is respectievelijk te wijten aan constructieve en destructieve interferentie. Bron: Wikimedia Commons.

Young observeerde een onderscheidend patroon van alternatieve lichte en donkere lijnen. Wanneer lichtbronnen destructief interfereren, zijn de lijnen donker, maar als ze dat constructief doen, zijn de lijnen duidelijk.

Een ander interessant interferentie -voorbeeld is zeepbellen. Dit zijn zeer dunne films, waarin de interferentie optreedt omdat het licht wordt gereflecteerd en gebroken op de oppervlakken die de soapfilm beperken, zowel boven als hieronder.

Figuur 5. Op een dunne zeepfilm wordt een interferentiepatroon gevormd. Bron: PxFuel.

Zoals de film dik is. Het resultaat is een kleurenpatroon als het invallende licht wit is.

Het is omdat het witte licht niet monochromatisch is, maar het bevat alle golflengten (frequenties) van het zichtbare spectrum. En elke golflengte ziet eruit als een andere kleur.

Het kan je van dienst zijn: lichtgevende lichamen: kenmerken en hoe ze hun eigen licht genereren

Oefening opgelost

Twee identieke luidsprekers die door dezelfde oscillator worden bediend, zijn 3 meter gescheiden en één luisteraar ligt op 6 meter afstand van het middelpunt van de scheiding tussen luidsprekers, op punt of.

Verplaats vervolgens naar punt P, op een loodrechte afstand van 0.350 van het punt of, zoals getoond in de figuur. Daar stopt voor het eerst niet meer naar het geluid. Wat is de golflengte waarin de oscillator uitzendt?

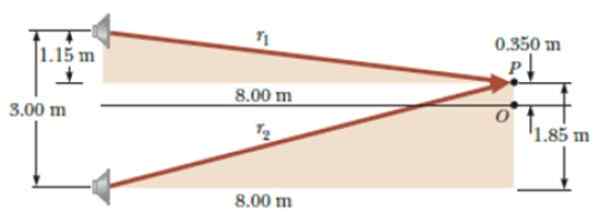Figuur 6. Diagram voor de oefening opgelost. Bron: Serway, r. Natuurkunde voor wetenschap en engineering.

Oplossing

De amplitude van de resulterende golf is 0, daarom is de interferentie destructief. Je moet:

Faseverschil = 2π x│r₁ - R₂│/ λ

Door de stelling van Pythagoras toegepast op de gearceerde driehoeken van de figuur:

R₁ = √1.vijftien² + 8² M = 8.08 m; R₂ = √1.85² + 8² M = 8.21 m

│R₁ - R₂│ = │8.08- 8.21 │ m = 0.13 m

De minima treden op in λ/2, 3λ/2, 5λ/2 ... De eerste komt overeen met λ/2, dan is van de formule voor het faseverschil::

λ = 2π x│r₁ - R₂│/ Faseverschil

Maar het faseverschil tussen de golven moet π zijn, zodat de amplitude_R = 2a cos (φ/2) wees dan nietig:

λ = 2π x│r₁ - R₂│/ π = 2 x 0.13 m = 0.26 m

Referenties

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 7. Golven en kwantumfysica. Uitgegeven door Douglas Figueroa (USB).
2. Fisicalab. Golf interferentie. Hersteld van: fisicalab.com.
3. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
4. Serway, r. Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
5. Wikipedia. Interferentie van het slaapblad. Bron: het is.Wikipedia.borg.