Willekeurig experimentconcept, voorbeeldruimte, voorbeelden

Er is sprake van willekeurig experiment Wanneer het resultaat van elke specifieke proef onvoorspelbaar is, kan zelfs wanneer de kans op het optreden van een bepaald resultaat kan worden vastgesteld.

Het moet echter worden verduidelijkt dat het niet mogelijk is om hetzelfde resultaat te reproduceren van een willekeurig systeem met dezelfde initiële parameters en voorwaarden in elke proef met het experiment.

Figuur 1. DICE -lancering is een willekeurig experiment. Bron: Pixabay.

Een goed voorbeeld van een willekeurig experiment is de lancering van een dobbelstenen. Zelfs als u ervoor zorgt dat de dobbelstenen op dezelfde manier lanceren, wordt in elke poging een onvoorspelbaar resultaat verkregen. Het enige dat kan worden bevestigd, is dat het resultaat een van de volgende kan zijn: 1, 2, 3, 4, 5 of 6.

De lancering van een valuta is een ander voorbeeld van willekeurig experiment met slechts twee mogelijke resultaten: gezicht of zegel. Hoewel de valuta van dezelfde hoogte en op dezelfde manier wordt gelanceerd, zal de toevallige factor altijd aanwezig zijn, wat resulteert in onzekerheid voor elke nieuwe poging.

Het tegenovergestelde van een willekeurig experiment is een deterministisch experiment. Het is bijvoorbeeld bekend dat elke keer dat water op zeeniveau wordt gekookt, de kooktemperatuur 100 ºC is. Maar het gebeurt nooit dat, met behoud van dezelfde omstandigheden, het resultaat soms 90 ºC, nog eens 12 0ºC en soms 100 ºC is.

[TOC]

Voorbeeldruimte

De set van alle mogelijke resultaten van een willekeurig experiment wordt genoemd voorbeeldruimte. In het willekeurige experiment van de lancering van een dobbelstenen is de voorbeeldruimte:

D = 1, 2, 3, 4, 5, 6.

Van zijn kant is de voorbeeldruimte bij de lancering van een valuta:

M = Face, Seal.

Evenement of evenement

In een willekeurig experiment, a evenement Het is het optreden of niet van een bepaald resultaat. Bijvoorbeeld, in het geval van de lancering van een valuta, is een evenement of evenement om duur te zijn.

Kan u van dienst zijn: homologe kanten

Een ander evenement in een willekeurig experiment kan als volgt zijn: dat bij de lancering van een dobbelstenen een nummer minder dan drie wordt vrijgegeven.

In het geval dat de gebeurtenis plaatsvindt, is de set mogelijke resultaten de set:

E = 1, 2, 3

Op zijn beurt is dit een subset van de ruimte- of voorbeeldset:

M = 1, 2, 3, 4, 5, 6.

Voorbeelden

Hieronder staan ​​enkele voorbeelden die het bovenstaande illustreren:

voorbeeld 1

Neem aan dat twee munten worden gegooid, de een na de andere. Het wordt gevraagd:

a) Geef aan of het een willekeurig experiment is of integendeel een deterministisch experiment.

b) Wat is de steekproefruimte van dit experiment?

c) Geef de hele gebeurtenis A aan, die overeenkomt met het experiment heeft een gezichts- en stempelresultaat.

d) bereken de kans dat de gebeurtenis zich voordoet.

e) Zoek ten slotte de kans dat gebeurtenis B: niet op het resultaat verschijnen.

Oplossing 

a) Het is een willekeurig experiment omdat er geen manier is om te voorspellen wat het resultaat zal zijn van een lancering van de twee munten.

b) De monsterruimte is de set van alle mogelijke resultaten:

S = (c, c), (c, s), (s, c), (s, s)

c) Gebeurtenis A, in het geval dat wordt gegeven, kan de volgende resultaten hebben:

A = (c, s), (s, c)

D) De kans op gebeurtenis A wordt verkregen door het delen van het aantal elementen van de set A tussen het aantal elementen van de set die overeenkomt met de monsterruimte:

P (a) = 2/4 = ½ = 0.5 = 50%

e) De set mogelijke resultaten die overeenkomen met gebeurtenis B (geen gezicht voor het resultaat verschijnen) is:

Kan u van dienst zijn: perfect vierkant trinomiaal

B = (s, s)

Dus de kans dat gebeurtenis B in een essay optreedt, is de verhouding tussen het aantal mogelijke resultaten van B tussen het aantal totale gevallen:

P (b) = ¼ = 0.25 = 25%.

Voorbeeld 2

Een tas bevat 10 witte knikkers en 10 zwarte knikkers. Uit de tas worden ze willekeurig verwijderd en zonder achtereenvolgens naar binnen drie knikkers te kijken. 

a) Bepaal de steekproefruimte van dit willekeurige experiment.

b) Bepaal de set resultaten die overeenkomen met de gebeurtenis, waardoor er na het experiment twee zwarte knikkers zijn.

c) Evenement B is om ten minste twee zwarte knikkers te verkrijgen, bepaal set B van resultaten voor dit evenement.

D) Wat is de kans dat de gebeurtenis plaatsvindt?

e) Vind de kans dat gebeurtenis B.

f) Bepaal de kans dat het resultaat van het willekeurige experiment is dat ten minste één zwart marmer. Dit evenement wordt C genoemd.

Figuur 2. Zwarte en zwarte knikkers voor willekeurige experimenten. Bron: NeedPix.

Oplossing voor

Om de monsterruimte te bouwen, is het handig om een ​​boomdiagram te maken, zoals dat getoond in figuur 3:

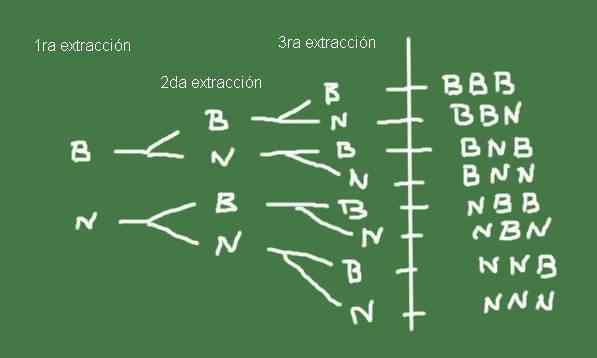figuur 3. Boomdiagram bijvoorbeeld 2. Bereid door Fanny Zapata.

De ω set mogelijke resultaten van het extraheren van drie knikkers uit een tas met hetzelfde aantal zwarte en zwarte knikkers, is precies de steekproefruimte van dit willekeurige experiment.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)

Oplossing B

De set mogelijke resultaten die overeenkomen met gebeurtenis A, die bestaat uit het hebben van twee zwarte knikkers is:

Kan u van dienst zijn: som van riemann: geschiedenis, formules en eigenschappen, oefeningen

A = (b, n, n), (n, b, n), (n, n, b)

Oplossing C

Evenement B wordt gedefinieerd als: "om ten minste twee zwarte knikkers te hebben nadat hij de willekeurige extractie van drie van hen heeft gemaakt". De set mogelijke resultaten voor gebeurtenis B is:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Oplossing D

De kans op gebeurtenis A is de verhouding tussen het aantal mogelijke resultaten voor deze gebeurtenis, en het totale aantal mogelijke resultaten, dat wil zeggen het aantal monsterruimte -elementen.

P (a) = n (a) / n (ω) = 3/8 = 0.375 = 37.5%

Dus er zijn 37.5% waarschijnlijkheid van twee zwarte knikkers na willekeurig drie knikkers uit de tas geëxtraheerd. Maar merk op dat we op geen enkele manier het exacte resultaat van het experiment kunnen voorspellen.

Oplossing e

De kans dat gebeurtenis B wordt gegeven, bestaande uit ten minste één zwart marmer is:

P (b) = n (b) / n (ω) = 4/8 = 0.5 = 50%

Dit betekent dat de mogelijkheid van gebeurtenis B gelijk is aan de waarschijnlijkheid die niet opkomt. 

Oplossing f

De kans om ten minste één zwart marmer te verkrijgen, na het extraheren van drie, is gelijk aan 1 minder de kans dat het resultaat "de drie witte knikkers" is.

P (C) = 1 - P (B B B) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Nu kunnen we dit resultaat verifiëren en opmerken dat het aantal mogelijkheden gezien de gebeurtenis C gelijk is aan het aantal elementen van de mogelijke resultaten voor gebeurtenis C:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (ω) = ⅞ = 87.5%

Referenties

1. Canalphi. Willekeurig experiment. Hersteld van: YouTube.com.
2. Mathemovil. Willekeurig experiment. Hersteld van: YouTube.com
3. Pishro Nick H . Inleiding tot waarschijnlijkheid. Opgehaald uit: waarschijnlijkheid Course.com
4. Ross. Waarschijnlijkheid en statistieken voor ingenieurs. MC-GRAW HILL.
5. Wikipedia. Experiment (waarschijnlijkheidstheorie). Opgehaald uit: in.Wikipedia.com
6. Wikipedia. Deterministische gebeurtenis. Hersteld van: is. Wikipedia.com
7. Wikipedia. Willekeurig experiment. Hersteld van: is.Wikipedia.com