Clausius-Claapeyron-vergelijking Waar is het voor, voorbeelden, oefeningen
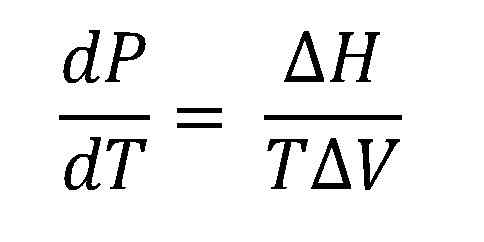
- 1297
- 184
- Dewey Powlowski
De Clausius-Claapeyron-vergelijking Het is er een die de veranderingen in de dampdruk en de temperatuur, in een fase of verandering van toestandovergang relateert. Geldt sublimaties, verdampingen, fusies of zelfs in veranderingen in kristallijne fasen. Het is vermeldenswaard dat deze vergelijking van toepassing is op een zuivere stof die in evenwicht is.
Deze vergelijking is afgeleid van de thermodynamische wetten en P-T-diagrammen voor een stof, waarbij de coëxistentie-lijn wordt waargenomen; dat wat twee verschillende fasen scheidt (vloeistofvapor, vaste vloeistof, enz.)). Om deze lijn over te dragen, is winst of verlies van warmte noodzakelijk, zoals verdamping enthalpie, ΔHDapper.
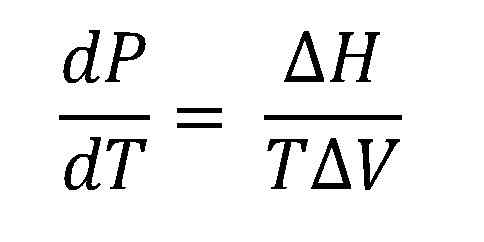 Clausius-Claapeyron-vergelijking. Bron: Gabriel Bolívar.
Clausius-Claapeyron-vergelijking. Bron: Gabriel Bolívar. De hogere afbeelding toont de Clausius-Claapeyron-vergelijking voordat hij wordt geïntegreerd. Normaal gesproken wordt het meestal toegepast op vloeistofvaporsystemen, waarbij AH wordt gebruiktDapper en u wilt berekenen wat de vloeibare dampdruk op een bepaalde temperatuur zal zijn. Het dient ook om de ΔH te berekenenDapper van een bepaalde vloeistof in een temperatuurbereik.
Clausisu-Claapeyron-vergelijking wordt ook vrij vaak gebruikt om drukveranderingen in vluchtige vaste stoffen te bestuderen; dat wil zeggen, de sublimatie -enthalpie wordt beschouwd, ΔHsub.
[TOC]
Wat is de clausisu-claapeyron-vergelijking voor?
Berekening van druk van druk en enthalpieën van verdamping
Uit de vergelijking van Clausius-Claapeyron van bovenaf worden eindelijk enkele wiskundige overwegingen gemaakt om eindelijk een integratie uit te voeren. Voor een vloeistofdampsysteem wordt bijvoorbeeld aangenomen dat ΔHDapper Het varieert niet met de temperatuur en dat AV exclusief overeenkomt met het volume van de stoom, veracht het volume van de vloeistof (Vstoom-Vvloeistof = Vstoom)).
Ervan uitgaande dat stoom zich als een ideaal gas en integratie gedraagt, wordt de vergelijking van Clausius-Claapyron geïntegreerd verkregen:
Kan u van dienst zijn: vervluchtiging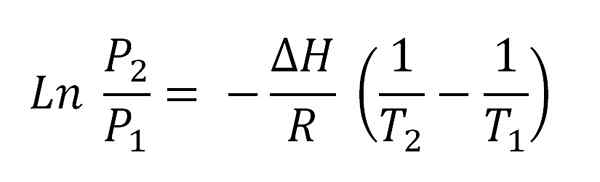 Clausius-ClaapEyron-vergelijking geïntegreerd.
Clausius-ClaapEyron-vergelijking geïntegreerd. Deze vergelijking komt overeen met die van een lijn die grafisch is als:
Ln p vs 1/t
En wiens negatieve helling is (ΔH/R). Om aan deze vergelijking te voldoen, moet ΔH daarom constant zijn in het temperatuurinterval (t2-T1) waarin stoomdrukken worden gemeten in evenwicht met de vloeistof.
Op deze manier, als wordt aangenomen dat AH weinig varieert binnen kleine temperatuurintervallen, is het mogelijk om de vergelijking van deze lijn te gebruiken om veranderingen in de dampdruk van een vloeistof te voorspellen; En nog meer, u kunt de verdamping ervan bepalen.
Hoe groter de Temperatures -intervallen beschouwd, hoe grootste de afwijking van deze vergelijking van de experimentele gegevens, en hoe minder het zal worden vervuld.
Bepaling van faseveranderingen
Aldus wordt de vergelijking van Clausius-Claapeyron de ontwikkeling van een raaklijn naar de coëxistentie-lijn tussen twee fysieke fasen, die wordt waargenomen in elk P-T-diagram voor een stof.
Als er een faseverandering optreedt, is er een verandering op de helling en zal ΔH niet hetzelfde zijn. Daarom, wanneer sterke afwijkingen worden bewezen en de vergelijking mislukt, is het een teken dat de stof in het temperatuurinterval een andere faseverandering ervaart. Dat wil zeggen, het houdt op een vloeistofdampersysteem te zijn, omdat het wordt doorgegeven aan de coëxistentielijn.
Gebruik voorbeelden
- De Clausius-Claapeyron-vergelijking is in meteorologie gebruikt om het gedrag van de wolken te bestuderen, zelfs die aanwezig zijn op andere planeten of manen met atmosferen.
Kan u dienen: gluconzuur: structuur, eigenschappen, synthese, gebruik- Het is gebruikt bij het bepalen van de fusie -enthalpie van verschillende metalen zoals natrium en gallium, en om hun dampdruk te extrapoleren bij zeer hoge temperaturen.
- Het is ook gebruikt om de enthalpie van verdamping van stoffen zoals gasvormig chloor, koolstoftetrachloride, vloeibaar water, ijs en jodium te bepalen.
- Het heeft ook gediend om faseveranderingen in kristallijne structuren te bestuderen. In dit laatste voorbeeld ziet de geïntegreerde vergelijking van Clausius-Clapeyron er opmerkelijk anders uit, omdat dezelfde overwegingen die worden genomen voor het vloeistofdampersysteem niet kunnen worden gemaakt voor ΔV. De volumevariaties van de ene fase naar de andere zijn deze keer klein.
Opgeloste oefeningen
- Oefening 1
De ijsdampdruk is 4.58 torr bij 0 ° C en 1.95 Torr A -10 ° C. Wat is uw sublimatie -enthalpie in dat temperatuurbereik?
Merk op dat we twee druk en twee temperaturen hebben:
P1 = 4.58 Torr
P2 = 1.95 Torr
T1 = 0 ° C + 273 = 273 K
T2 = -10 ° C + 273 = 263 K
We converteren de temperatuureenheden van ° C naar K, omdat de constante R van gassen k in zijn eenheden heeft:
R = 8.314 J/K
Daarom gebruiken we de geïntegreerde Clausius-Claapeyron-vergelijking en duidelijk AHsub, die zouden blijven als:
AHsub = -Rln (p2/P1) / (1 / t2 - 1 /t1))
Voor meer comfort zal het alleen doorgaan door de cijfers, maar wetende dat de uiteindelijke eenheid de Joule zal zijn:
AHsub = -(8.314) ln (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Of 51.07 J die weinig decimalen overwegen. Deze waarde presenteert oscillaties afhankelijk van intervallen t2-T1 en van bepaalde stoomdruk.
- Oefening 2
Het kookpunt van ethanol bij een druk van 760 Torr (1 atm) is 78.3 ° C, en de verdamping enthalpie is 39.3 kJ. Wat zal uw stoomdruk zijn bij een temperatuur van 46 ° C?
Het kan u van dienst zijn: tantalus: structuur, eigenschappen, gebruik, verkrijgenWe identificeren de gegevens:
P1 = 760 TORR
P2 = ?
T1 = 78.3 ° C + 273 = 351.3 k
T2 = 46 ° C + 273 = 319 K
AHDapper = 39.3 kJ of 39300 J
Dus we moeten p wissen2 van de geïntegreerde Clausius-Claapeyron-vergelijking. Nogmaals, de eenheden worden weggelaten voor comfort en de berekeningen worden stap voor stap ontwikkeld:
Ln (p2/P1) = -(ΔHDapper/R) (1/t2 - 1/t1))
Ln (p2/760) = -(39300/8.314) (1/319 - 1/351.3)
Ln (p2/760) = -1.36
Het toepassen van de exponentiële functie aan beide zijden van de vergelijking om p te kunnen wissen2 we zullen hebben:
E (LN P2/760) = E(-1.36)
P2/760 = 0.256
P2 = 0.256 (760)
= 195 Torr
Bij een lagere temperatuur (46 ° C), lagere stoomdruk (195 torr). In feite hebben de ethanol een druk van 760 torr tot 78.3 ° C, we hebben het over het normale kookpunt. Dit is het gedrag dat wordt verwacht voor alle vloeistoffen
Over het algemeen bestaan Clausius-Claapeyron-oefeningen van dit type uit het opruimen van P2, T2 of ΔH van verdamping of sublimatie. De berekeningen veranderen aanzienlijk wanneer AV ook moet worden overwogen, vooral als het gaat om vaste-vloeistofsystemen of saldi.
Referenties
- Whitten, Davis, Peck & Stanley. (2008). Scheikunde. (8e ed.)). Cengage leren.
- Wikipedia. (2020). Clausius-Claapeyron-relatie. Opgehaald uit: in.Wikipedia.borg
- San José State University. (S.F.)). De Clausius-Claapeyron-vergelijking:
SO -afleiding en toepassing in meteorologie. Hersteld van: SJSU.Edu - Bodner -groep. (S.F.)). De Clausius-Claapeyron-vergelijking. Opgehaald uit: Chemed.Chem.Purdue.Edu
- Chieh c. & Censulo a. (18 mei 2020). Clausius-Claapeyron-vergelijking. Chemistry Libhethexts. Hersteld van: chem.Librhetxts.borg
- Walter J. Moore. (1962). Fysische chemie. (Vierde druk). Longmans.
- « 7 gedichten over de omgeving van bekende auteurs
- Leren voor ontdekkingstheorie, voorbeelden, activiteiten »

