Rechthoekige coördinaten voorbeelden en oefeningen opgelost

De rechthoekige coördinaten o Cartesian zijn die welke worden verkregen wanneer deze orthogonaal worden geprojecteerd op de drie Cartesiaanse assen x, y, z een punt in de drie -dimensionale ruimte.

Cartesiaanse assen zijn onderling loodrecht georiënteerd recht. In het Cartesiaanse coördinatensysteem worden drie reële getallen die de rechthoekige coördinaten zijn toegewezen aan elk punt in de ruimte toegewezen.

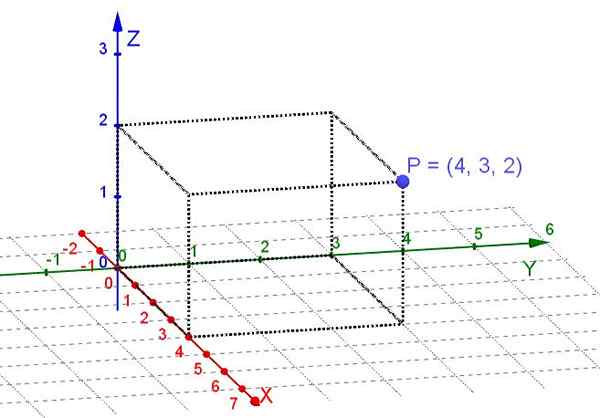
Figuur 1. Rechthoekige coördinaten van punt P (eigen uitwerking)

Een vliegtuig is een subruimte van drie -dimensionale ruimte. In het geval van het overwegen van punten op een vlak, is het voldoende om een ​​paar loodrechte assen x te kiezen, en als een Cartesiaans systeem. Dan worden op elk punt in het vlak twee reële getallen aan hem toegewezen dat zijn rechthoekige coördinaten zijn.

[TOC]

Oorsprong van rechthoekige coördinaten

De rechthoekige coördinaten werden oorspronkelijk voorgesteld door de Franse wiskundige René Descartes (1596 en 1650), daarom ontvangen ze de denominatie van Cartesiërs.

Met dit idee van Descartes zijn de punten van het vlak en de ruimte getallen toegewezen, zodat de geometrische figuren een algebraïsche vergelijking hebben geassocieerd en de klassieke geometrische stellingen kunnen worden aangetoond. Met Cartesiaanse coördinaten werd analytische geometrie geboren.

Het Cartesiaanse vlak

Als in een vlak twee loodrechte lijnen worden gekozen die op één punt kruisen of; en als ook elke lijn een richting en een numerieke schaal wordt toegewezen tussen opeenvolgende gelijkwaardige punten, is er dan een Cartesiaans systeem of plan waarin elk punt van het vlak is geassocieerd met een geordend paar van twee reële getallen die de projecties zijn respectievelijk op de x en y assen.

Punten A = (3, 2); B = (-2, 3); C = (-2, -3) en d = (3, -3) worden weergegeven in het Cartesiaanse vlak zoals hieronder getoond:

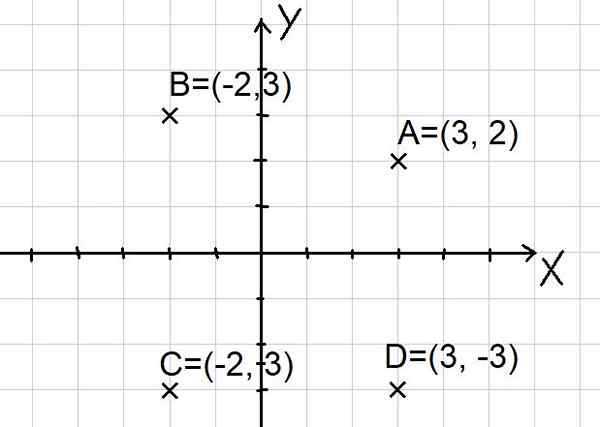Figuur 2. Punten op het Cartesiaanse vliegtuig. (Eigen uitwerking)

Merk op dat de twee x- en y -assen het vlak verdelen in vier sectoren die kwadranten worden genoemd. Punt A bevindt zich in het eerste kwadrant, de B in het tweede kwadrant, de C in het derde kwadrant en punt D in het vierde kwadrant.

Kan u van dienst zijn: populatie en steekproef

Afstand tussen twee punten

De afstand tussen twee punten A en B van het Cartesiaanse vlak is de lengte van het segment dat ze verenigt. Deze afstand kan analytisch als volgt worden berekend:

D (a, b) = √ (bx - ax)^2 + (door - ay)^2)

De voorste formule wordt verkregen door de stelling van Pythagoras toe te passen.

Het toepassen van genoemde formule op punten a, b van figuur 2 is:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

Dat wil zeggen, die d (a, b) = 5,10 eenheden. Merk op dat de afstand is verkregen zonder de noodzaak om met een regel te meten, is een volledig algebraïsche procedure gevolgd.

Analytische expressie van een lijn

Rechthoekige coördinaten maken de analytische weergave mogelijk van fundamentele geometrische objecten zoals het punt en de lijn. Twee punten A en B definiëren een enkele lijn. De helling van de lijn wordt gedefinieerd als het quotiënt tussen het verschil in coördinaten en punt B minder, gedeeld door het verschil in de x -coördinaten van punt B minder de a:

in behandeling = (door - ay)/(bx - ax)

Een elk punt van coördinaten (x, y) dat tot de lijn (AB) behoort, moet dezelfde helling hebben:

in behandeling = (y - ay)/(x - ax)

De vergelijking die wordt verkregen door de gelijkheid van de hellingen is de analytische of algebraïsche weergave van de lijn die door de punten A en B passeert:

(y - ay)/(x - ax) = (door - ay)/(bx - ax).

Als u voor A en B wordt ingenomen, zijn de rechthoekige coördinaten van figuur 2:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

In dit specifieke geval is er een lijn met een negatieve helling -⅕, wat betekent dat het zich op een punt van de lijn bevindt en de X -coördinaat in een eenheid verhoogt, de coördinaten en afneemt in 0,2 eenheden. 

Kan u van dienst zijn: toroid of toro dona

De meest gebruikelijke manier om de vergelijking van de lijn in het vlak te schrijven is met de coördinaat en duidelijk als een functie van variabele x:

y = -(1/5) x + 13/5 

Voorbeelden

voorbeeld 1

Verkrijg door analytische methoden de afstand tussen punten C en A, zijnde de rechthoekige coördinaten van C = (-2, -3) en die van A = (3.2).

De formule van de Euclidische afstand tussen deze twee punten is als volgt geschreven:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Het vervangen van de overeenkomstige rechthoekige coördinaten die u hebt:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7.07

Voorbeeld 2

Verkrijg de vergelijking van de lijn die door punt C van coördinaten (-2, -3) en het punt P van coördinaat (2, 0).

Eerst wordt de helling van de CP -lijn verkregen:

in behandeling = (0 -(-3)) / (2 -( -2)) = ¾ 

Een elk punt q van generieke rechthoekige coördinaten (x, y) die tot de CP -lijn behoort, moet dezelfde helling hebben:

in behandeling = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

Dat wil zeggen dat de vergelijking van de CP -lijn is:

(Y +3) / (x +2) = ¾

Een alternatieve manier om de vergelijking van de CP -lijn te schrijven, is opruimen en::

y = ¾ x - 3/2 

Opgeloste oefeningen

Oefening 1

Verkrijg de rechthoekige coördinaten van het snijpunt tussen de lijnen y = - (1/5) x + 13/5 en de lijn y = ¾ x - 3/2.

Oplossing: per definitie deelt het snijpunt van de twee lijnen dezelfde rechthoekige coördinaten. Daarom is coördinaten en op het punt van kruising identiek voor beide lijnen:

-(1/5) x + 13/5 = ¾ x - 3/2

Wat leidt tot de volgende uitdrukking:

Kan u van dienst zijn: rechthoek trapezoid: eigenschappen, relaties en formules, voorbeelden

(¾ + ⅕) x = 13/5 +3/2

Het oplossen van de som van breuken wordt verkregen:

19/20 x = 41/10

X:

x = 82/19 = 4.32

Om de waarde en kruising te verkrijgen, wordt de X -waarde verkregen in een van de lijnen vervangen:

y = ¾ 4,32 - 3/2 = 1,74

Dit betekent dat de gegeven lijnen worden onderschept op punt I van coördinaten I = (4.32; 1,74).

Oefening 2

Verkrijg de omtrekvergelijking die door het rechthoekige coördinaatpunt R (3, 4) gaat en die een centrum heeft bij de oorsprong van coördinaten.

Oplossing: Radio R is de afstand van punt R tot oorsprong of coördinaten (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Dat wil zeggen, het is een straal 5 cirkel 5 gecentreerd op (0,0).

Een elk punt P (x, y) van de omtrek moet dezelfde afstand 5 tot het midden hebben (0, 0) voor wat kan worden geschreven:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

Het is te zeggen:

√ (x^2 + y^2) = 5

Om de vierkantswortel te elimineren, worden beide leden van gelijkheid rustig achtergelaten:

x^2 + y^2 = 25

Wat is de omtrekvergelijking.

Met dit voorbeeld wordt het vermogen van het rechthoekige coördinatensysteem geïllustreerd, waardoor geometrische objecten kunnen worden bepaald, zoals de omtrek zonder het gebruik van papier, potlood en kompas. De omtrek die alleen door algebraïsche methoden wordt gevraagd, is bepaald.

Referenties

1. Arfken G en Weber H. (2012). Wiskundige methoden voor natuurkundigen. Een uitgebreide gids. 7e editie. Academische pers. ISBN 978-0-12-384654-9
2. CC -berekening. Rechthoekige coördinaten opgeloste problemen. Teruggewonnen uit: berekening.DC
3. Weisstein, Eric W. "Cartesiaanse coördinaten.”Van Mathworld-a Wolfram Web. Hersteld van: Mathworld.Wolfraam.com
4. Wikipedia. Cartesisch coördinatenstelsel. Opgehaald uit: in.Wikipedia.com