Sferische coördinaten Voorbeelden en oefeningen opgelost

De bolvormige coördinaten Ze zijn een puntlocatiesysteem in de drie -dimensionale ruimte bestaande uit een radiale coördinaat en twee hoekcoördinaten die polaire coördinaat en azimutale coördinaat worden genoemd.

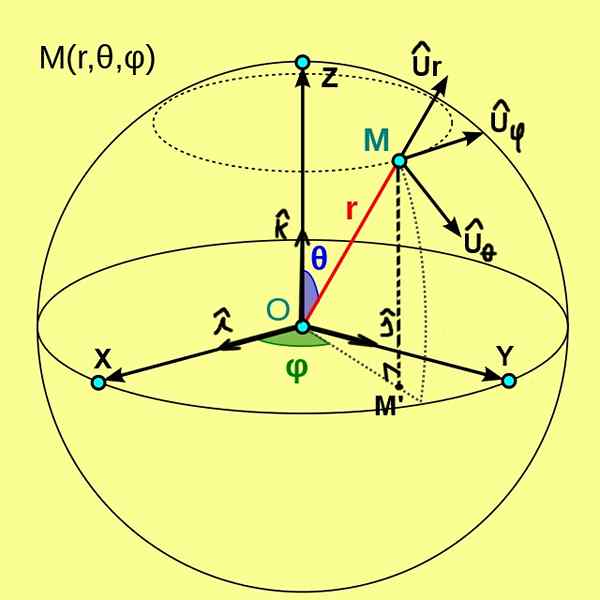
In figuur 1, die we hieronder zien, worden de sferische coördinaten (r, θ, φ) van een punt m getoond. Deze coördinaten worden verwezen naar een orthogonaal systeem van Cartesiaanse assen X, Y, Z van oorsprong of.

Figuur 1. Sferische coördinaten (r, θ, φ) vanaf een punt m. (Wikimedia Commons)

In dit geval is coördinaat R van punt M de afstand van dat punt tot de oorsprong of. De polaire coördinaat θ vertegenwoordigt de hoek tussen de positieve semi -as z en de vectorradius om. Terwijl de azimutale coördinaat φ de hoek is tussen de positieve semi -as x en de vectorradius om ', is de orthogonale projectie van m op het xy -vlak.

De radiale coördinaat R heeft alleen positieve waarden, maar als een punt zich bij de oorsprong bevindt, dan r = 0. De polaire coördinaat θ neemt als een minimale waarde 0º voor punten die zich op de positieve semi -trib bevinden. Ten slotte neemt de azimutale coördinaat φ als een minimale waarde 0º en maximaal 360º niveau.

0 ≤ r < ∞

0 ≤ θ ≤ 180º

0 ≤ φ  < 360º

[TOC]

Verandering van coördinaten

Vervolgens zullen de formules die de Cartesiaanse coördinaten (x, y, z) van een punt m toestaan, uitgaande van de sferische coördinaten van hetzelfde (r, θ, φ) punt:

x = r sen (θ) cos (φ)

y = r sen (θ) sin (φ) 

z = r cos (θ)

Op dezelfde manier is het nuttig om de relaties te vinden om van de Cartesiaanse coördinaten (x, y, z) te gaan van een punt gegeven aan de sferische coördinaten van dat punt:

R = √ (x^2 + y^2 + z^2)

θ = arcan (√ (x^2 + y^2) / z)

Kan u van dienst zijn: discrete willekeurige variabele

φ = arctan (y / x)

Vectorbasis in bolvormige coördinaten

Van de sferische coördinaten wordt een ortonormale basis van basisvectoren gedefinieerd, die worden aangegeven door Ur, Uθ, Uφ. Figuur 1 toont deze drie eenheidsvectoren, die de volgende kenmerken hebben:

- Ur Het is de eenheidsvector die op de radiale lijn raakt θ = ctte en φ = ctte;

- Uθ Het is de eenheid tangent vector aan de boog φ = ctte en r = ctte;

- Uφ Het is de eenheidsvector die raakt naar boog r = ctte en θ = ctte.

Lijn- en volume -elementen in bolvormige coördinaten

De vectorpositie van een punt in de ruimte in bolvormige coördinaten is als volgt geschreven:

R = r Ur

Maar een oneindigse variatie of verplaatsing van een punt in de drie -dimensionale ruimte, in deze coördinaten wordt uitgedrukt door de volgende vectorrelatie:

DR = DR Ur + r dθ Uθ + r sen (θ) dφ Uφ

Ten slotte is er een oneindig veel volume DV in de sferische coördinaten geschreven:

dv = r^2 sin (θ) dr dθ dφ

Deze relaties zijn zeer nuttig voor de berekening van lijnintegralen en volume in fysieke situaties die bolvormige symmetrie hebben.

Relatie met geografische coördinaten

Geografische coördinaten is duidelijk dat ze dienen om plaatsen op het aardoppervlak te vinden. Dit systeem gebruikt de coördinaten van breedtegraad en lengte om de positie op het aardoppervlak te vinden.

In het geografische coördinatensysteem wordt het aardoppervlak verondersteld.

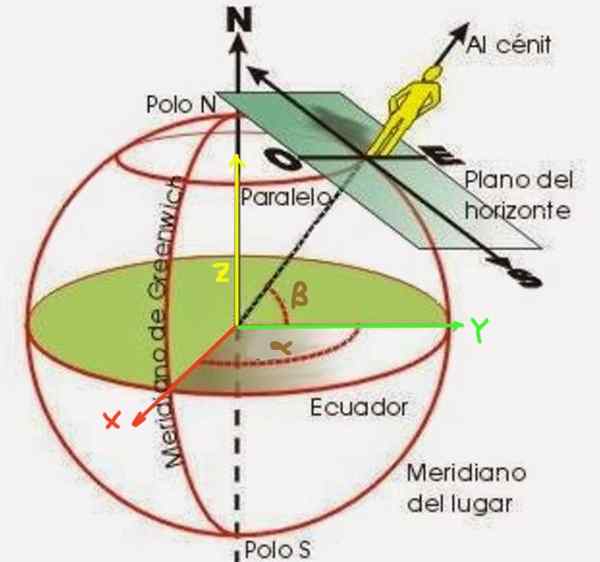Figuur 2. Lengte α en β -breedtegraad van een waarnemer op het aardoppervlak.

De β -breedtegraad is een hoek gevormd door een straal die begint vanuit het midden van de aarde tot het punt dat u wilt positioneren. Het wordt gemeten uit het equatoriale vlak, zoals weergegeven in figuur 2. Aan de andere kant is de lengte α de hoek dat de meridiaan van het punt dat vorm plaatst ten opzichte van de nul meridiaan (bekend als Greenwich Meridian).

Kan u van dienst zijn: relatieve waarde

Latitude kan noord- of zuidelijke breedtegraad zijn, afhankelijk van of de plaats die zich bevindt op het noordelijk halfrond of op het zuidelijk halfrond ligt. Evenzo kan de lengte het westen zijn of dit, afhankelijk van of de locatie ten westen of ten oosten van de nul meridiaan is.

Formules om te veranderen van geografisch naar bolvormig

Om deze formules te verkrijgen, is het eerste om een ​​coördinatensysteem op te zetten. Het XY -vlak wordt gekozen om samen te vallen met het equatoriale vlak, is de positieve semi -as X die van het midden van de aarde en door de nul meridiaan gaat. Op zijn beurt gaat de as en gaat door de 90º en Meridian. Het aardoppervlak heeft RT -radio.

Met dit coördinatensysteem zijn geografische tot bolvormige transformaties dus:

αEβN → (rt, θ = 90º-β, φ = α)

αoβN → (rt, θ = 90º-β, φ = 360º-a)

αEβ → (rt, θ = 90º+β, φ = α)

αOβS → (rt, θ = 90º+β, φ = 360º-a) 

Voorbeelden

voorbeeld 1

De geografische coördinaten van Palma de Mallorca (Spanje) zijn:

Oostlengte 38.847º en noordelijke breedtegraad 39.570º. Om de sferische coördinaten te bepalen die overeenkomen met Palma de Mallorca, wordt de eerste van de formules van de vorige sectie -formules toegepast:

38,847ºe39,570ºN → (r = 6371 km, θ = 90º-39,570º, φ = 38.847º)

Dan zijn de sferische coördinaten:

Palma de Mallorca: (r = 6371 km, θ = 50.43º, φ = 38,85º)

In de vorige reactie is R gelijk aan de gemiddelde straal van de aarde ingenomen.

Voorbeeld 2

Wetende dat de Falkland -eilanden (Falkland) geografische coördinaten hebben 59ºo 51,75ºS, bepaalt u de overeenkomstige polaire coördinaten. Vergeet niet dat de x -as van het midden van de aarde naar de 0º meridiaan en op het equatoriale vlak gaat; de y -as ook in het equatoriale vlak en door de 90º West -meridiaan; Eindelijk de Z-as op de as van terrestrische rotatie in de zuid-noordrichting.

Kan u van dienst zijn: Curtosis: definitie, typen, formules, waarvoor bijvoorbeeld

Om vervolgens de overeenkomstige sferische coördinaten te vinden, gebruiken we de formules die in de vorige sectie worden gepresenteerd:

59ºo 51,75ºS → (r = 6371 km, θ = 90º+51,75º, φ = 360º-59º) dat wil zeggen

Malvinas: (r = 6371 km, θ = 141,75º, φ = 301º)

Opdrachten

Oefening 1

Vind de Cartesiaanse coördinaten van Palma de Mallorca in het Cartesiano XYZ -referentiesysteem getoond in figuur 2.

Oplossing: Eerder werden in voorbeeld 1 de sferische coördinaten verkregen op basis van de geografische coördinaten van Palma de Mallorca. Zodat de hierboven gepresenteerde formules kunnen worden gebruikt om van bolvormig naar Cartesians te gaan:

x = 6371 km Sen (50,43º) Cos (38,85º)

Y = 6371 km sen (50,43º) sen (38,85º) 

Z = 6371 km cos (50,43º)

Het uitvoeren van de overeenkomstige berekeningen zijn:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Oefening 2

Vind de Cartesiaanse coördinaten van de Falkland -eilanden in het Cartesiano XYZ -referentiesysteem getoond in figuur 2.

Oplossing: Eerder in Voorbeeld 2 werden de sferische coördinaten verkregen op basis van de geografische coördinaten van de Falkland -eilanden. Zodat de hierboven gepresenteerde formules kunnen worden gebruikt om van bolvormig naar Cartesians te gaan:

x = 6371 km sen (141,75º) cos (301º)

y = 6371 km sen (141,75º) sen (301º) 

Z = 6371 km cos (141,75º)

Het uitvoeren van de overeenkomstige berekeningen wordt verkregen:

Falkland -eilanden: (x = 2031 km, y = -3381 km, z = -5003)

Referenties

1. Arfken G en Weber H. (2012). Wiskundige methoden voor natuurkundigen. Een uitgebreide gids. 7e editie. Academische pers. ISBN 978-0-12-384654-9
2. CC -berekening. Opgeloste cilindrische en bolvormige coördinaten. Teruggewonnen uit: berekening.DC
3. Astronomische workshop. Breedtegraad en lengte. Opgehaald uit: tarief.Blogspot.com/
4. Weisstein, Eric W. “Sferische coördinaten.”Van Mathworld-a Wolfram Web. Hersteld van: Mathworld.Wolfraam.com
5. Wikipedia. Sferisch coördinatensysteem. Opgehaald uit: in.Wikipedia.com
6. Wikipedia. Vectorvelden in cilindrische en bolvormige coördinaten. Opgehaald uit: in.Wikipedia.com