Waarschijnlijkheid axioma -typen, uitleg, voorbeelden, oefeningen

De axioma's van waarschijnlijkheid Het zijn wiskundige stellingen met betrekking tot de waarschijnlijkheidstheorie, die geen demonstratie verdienen. De axioma's werden in 1933 opgericht door de Russische wiskundige Andrei Kolmogorov (1903-1987) in zijn werk Fundamentals of waarschijnlijkheidstheorie en legde de basis van de wiskundige studie van waarschijnlijkheid.

Bij het uitvoeren van een bepaald willekeurig experiment ξ, is de monsterruimte degene met alle mogelijke resultaten van het experiment, ook wel genoemd evenementen. Elke gebeurtenis wordt aangeduid als a en p (a) is de kans om te gebeuren. Toen stelde Kolmogorov dat vast:

Figuur 1. Waarschijnlijkheid axioma's kunnen de kans berekenen om gokken te raken zoals roulette. Bron: Pixabay.

-Axioom 1 (geen negativiteit): De kans dat elke gebeurtenis zich voordoet, is altijd positief of nul, P (a) ≥0. Wanneer de kans op een gebeurtenis 0 is, wordt dit genoemd Onmogelijke gebeurtenis.

-Axioma 2 (zekerheid): op voorwaarde dat een gebeurtenis die tot E behoort, de kans op voorkomen 1 is, die we kunnen uitdrukken als P (E) = 1. Is wat bekend staat als een Veilig evenement, Sinds bij het uitvoeren van een experiment is er een resultaat met alle zekerheid.

-Axioom 3 (toevoeging): In het geval van twee of meer onverenigbare gebeurtenissen twee tot twee, geroepen₁, NAAR₂, NAAR₃..., de waarschijnlijkheid van het evenement om₁ meer de a₂ meer de a₃ Enzovoort, het is de som van de kansen dat elk afzonderlijk gebeurt.

Dit wordt uitgedrukt als: Vader₁ U a₂ U a₃ U ...) = P (a₁) + P (a₂) + P (a₃) +..

Figuur 2. De opmerkelijke Russische wiskundige Andrei Kolmogorov (1903-1987), die de basis legde voor axiomatische waarschijnlijkheid. Bron: Wikimedia Commons.

[TOC]

Voorbeeld

Waarschijnlijkheidsaxioma's worden veel gebruikt in veel toepassingen. Bijvoorbeeld:

Een klauw of tachuela wordt in de lucht gegooid, en wanneer de vloer valt, is er de optie om te vallen met de tip omhoog (u) of met de tip omlaag (d) (we zullen geen andere mogelijkheden overwegen). De voorbeeldruimte van dit experiment bestaat uit deze gebeurtenissen, vervolgens e = u, d.

Kan u van dienst zijn: Revolution Solids: volume, types, opgeloste oefeningenfiguur 3. In het experiment van het lanceren van de Tachuela zijn er twee gebeurtenissen van verschillende kansen: val met de tip omhoog of op de vloer. Bron: Pixabay.

Door de axioma's toe te passen die we hebben:

P (E) = 1 (Axioom 2)

Maar P (e) = p (u) + p (d) (Axioom 3), omdat deze gebeurtenissen onderling onverenigbaar of onsamenhangend zijn. De bug valt niet tegelijkertijd met de tip omhoog of omlaag, het is het ene of de ander, maar niet beide, omdat andere mogelijkheden worden overwogen. Dus:

P (u) + p (d) = 1

P (U) = 1 - P (D)

Als het even waarschijnlijk zal vallen met de tip omhoog of omlaag, P (u) = p (d) = ½ (Axioom 1). Het kan echter zijn dat vanwege de constructie en het ontwerp van de bug. Het kan bijvoorbeeld dat zijn P (u) = ¾ terwijl P (d) = ¼ (Axioom 1).

Merk op dat in beide gevallen de som van de kansen geeft 1. Axioma's geven echter niet aan hoe ze kansen kunnen worden toegewezen, althans niet volledig. Maar ze bevestigen wel dat het getallen tussen 0 en 1 zijn en dat, zoals in dit geval de som van alles is 1.

Manieren om waarschijnlijkheid toe te wijzen

Waarschijnlijkheidsaxiomen vormen geen methode om de waarde van waarschijnlijkheid toe te wijzen. Hiervoor zijn er drie opties die compatibel zijn met axioma's:

Laplace -regel

Elke gebeurtenis krijgt dezelfde kans om te gebeuren, dan wordt de kans op voorkomen gedefinieerd als:

P (a) = Aantal gevallen gunstig voor het evenement A/ aantal mogelijke gevallen

Wat is bijvoorbeeld de kans om een ​​aas te extraheren uit een dek van Franse kaarten? Het dek heeft 52 kaarten, 13 van elke stok en er zijn 4 sticks. Elke stok heeft 1 AS, dus in totaal zijn er 4 azen:

P (as) = ​​4/52 = 1/13

De regel van Laplace is beperkt tot eindige monsterruimtes, waar elke gebeurtenis even waarschijnlijk is.

Kan u van dienst zijn: discrete wiskunde

Relatieve frequentie

Hier moet het experiment herhaalbaar zijn, omdat de methode is gebaseerd op het uitvoeren van een groot aantal herhalingen.

Laten we herhalingen maken van het experiment ξ, waarvan we vinden dat n het aantal keren is dat een bepaalde gebeurtenis A voorkomt, dan is de kans dat deze gebeurtenis zal gebeuren:

P (a) = lim_{I → ∞} (geen van beide)

Waarbij n/i de relatieve frequentie van een gebeurtenis is.

Definieer p (a) op deze manier voldoet aan de axioma's van Kolmogorov, maar het heeft het ongemak dat veel tests moeten worden uitgevoerd, zodat de kans gepast is.

Subjectieve methode

Een persoon of een groep mensen kan ermee instemmen de kans toe te wijzen aan een evenement, via zijn eigen oordelen. Deze methode heeft het nadeel dat verschillende mensen verschillende kansen kunnen toewijzen aan hetzelfde evenement.

Oefening opgelost

In het experiment van het tegelijkertijd lanceren van 3 eerlijke valuta's, het verkrijgen van de kansen van de beschreven gebeurtenissen:

a) 2 gezichten en een kruis.

b) 1 gezicht en twee kruisen

c) 3 kruisen.

d) ten minste 1 gezicht.

Oplossing voor

De gezichten worden aangeduid met C en de kruisen met X. Maar er zijn verschillende manieren om twee gezichten en een kruis te krijgen. De eerste twee munten kunnen bijvoorbeeld vallen met gezicht en de derde met Cruz. Of de eerste kan vallen, het tweede kruis en het derde gezicht. En ten slotte kan de eerste een kruis zijn en de resterende gezichten.

Om de vragen te beantwoorden, is het noodzakelijk om alle mogelijkheden te kennen, die worden beschreven in een gereedschap genaamd boomdiagram of Waarschijnlijkheidsboom:

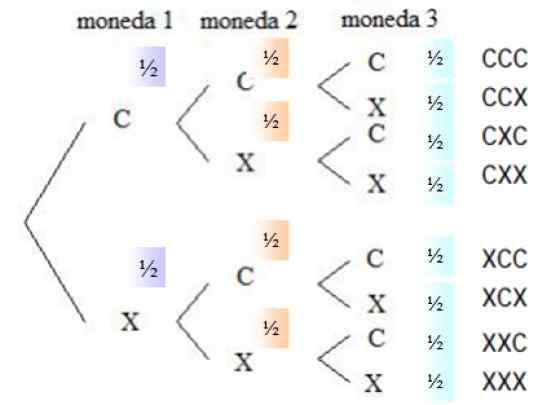Figuur 4. Boomdiagram voor gelijktijdige lancering van drie eerlijke munten. Bron: f. Zapata.

De kans dat in elke valuta duur is, is ½, hetzelfde gebeurt voor de kruisen, omdat de valuta eerlijk is. In de rechter kolom worden alle mogelijkheden om te lanceren vermeld, dat wil zeggen de voorbeeldruimte.

Kan u van dienst zijn: statistische variabelen

De combinaties die op de gevraagde gebeurtenis reageren, worden gekozen uit de steekproefruimte, omdat de volgorde waarin de gezichten verschijnen niet belangrijk is. Er zijn drie gunstige gebeurtenissen: CCX, CXC en XCC. De waarschijnlijkheid van elke gebeurtenis is:

P (CCX) = ½. ½ . ½ = 1/8

Hetzelfde gebeurt voor CXC- en XCC -gebeurtenissen, elk heeft 1/8 kans om te gebeuren. Daarom is de kans om precies 2 gezichten te verkrijgen de som van de waarschijnlijkheden van alle gunstige gebeurtenissen:

P (2 gezichten) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Oplossing B

Het vinden van de kans dat er precies twee kruisen zijn, is een analoog probleem voor de vorige, er zijn ook drie gunstige gebeurtenissen uit de voorbeeldruimte: CXX, XCX en XXC. Daarom:

P (2 kruisen) = 3/8 = 0.375

Oplossing C

Intuïtief weten dat de kans op het verkrijgen van 3 kruisen (of 3 gezichten) lager is. In dit geval is de gevraagde gebeurtenis XXX, aan het einde van de rechter kolom, waarvan de kans is:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Oplossing D

Er wordt gevraagd om ten minste 1 gezicht te verkrijgen, dit betekent dat 3 gezichten, 2 gezichten of 1 gezicht kunnen vertrekken. De enige gebeurtenis die hiermee onverenigbaar is, is er een waarin 3 kruisen uitkomen, wiens kans 0 is.125. Daarom is de gezochte kans:

P (minimaal 1 gezicht) = 1 - 0.125 = 0.875.

Referenties

1. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
2. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
3. Lipschutz, s. 1991. Schaum -serie: waarschijnlijkheid. McGraw Hill.
4. Obregón, ik. 1989.Theorie van waarschijnlijkheid. Redactionele limusa.
5. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.