Gegevens niet gegroepeerde voorbeelden en oefening opgelost

De Niet -groepen gegevens Zij zijn die, verkregen uit een onderzoek, nog niet worden georganiseerd door klassen. Wanneer het een beheersbaar aantal gegevens is, meestal 20 of minder, en er zijn weinig verschillende gegevens, kunnen ze worden behandeld als niet gegroepeerd en waardevolle informatie van hen extraheren.

De niet -geëxponeerde gegevens komen zoals uit de enquête of het onderzoek dat wordt uitgevoerd om ze te verkrijgen en daarom geen verwerking. Laten we eens kijken naar enkele voorbeelden:

Figuur 1. Niet -groepen gegevens komen rechtstreeks uit een onderzoek en zijn niet geclassificeerd. Bron: Pxhere.

-Resultaten van een intellectueel CI -examen bij 20 willekeurige studenten van een universiteit. De verkregen gegevens waren de volgende:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112,106

-Leeftijden van 20 werknemers van een zeer populaire cafetaria:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

-De gemiddelde definitieve aantekeningen van 10 studenten van een wiskundeklas:

3.2; 3.1; 2,4; 4.0; 3.5; 3.0; 3.5; 3.8; 4.2; 4.9

[TOC]

Data -eigenschappen

Er zijn drie belangrijke eigenschappen die een reeks statistische gegevens karakteriseren, zijn gegroepeerd of niet, namelijk:

-Positie, wat de neiging is van de gegevens die rond bepaalde waarden moeten worden gegroepeerd.

-Spreiding, Een indicatie van hoe verspreid of verspreid zijn, zijn de gegevens rond een bepaalde waarde.

-Vorm, Het verwijst naar de manier waarop de gegevens worden verdeeld, wat te zien is wanneer een grafiek ervan is geconstrueerd. Er zijn zeer symmetrische en ook bevooroordeelde krommen, hetzij links of rechts van een bepaalde centrale waarde.

Voor elk van deze eigenschappen zijn er een aantal maatregelen die ze beschrijven. Eenmaal verkregen, geven ze ons een panorama van gegevensgedrag:

-De meest gebruikte positiemaatregelen zijn rekenkundig gemiddelde of gewoon gemiddeld, mediaan en mode.

-In de dispersie worden het bereik, de variantie en de standaardafwijking vaak gebruikt, maar ze zijn niet de enige dispersiemaatregelen.

Kan u van dienst zijn: Homotecia

-En om de vorm te bepalen, worden het gemiddelde en de mediaan vergeleken door bias, zoals binnenkort zal worden gezien.

Berekening van gemiddelde, mediaan en mode

-Het rekenkundige gemiddelde, Ook bekend als gemiddeld en aangeduid als X, wordt het als volgt berekend:

X = (x₁ + X₂ + X₃ +... X_N) / N

Waar x₁, X₂,.. . X_N, zijn de gegevens en n is het totaal van hen. In de samenvatting van de som is er:

Hier vertegenwoordigt de index I gegevens 1, gegevens 2, gegevens 3 enzovoort, tot het bereiken van de enige, wat de laatste is.

-De mediaan Het is de waarde die in het midden van een geordende opeenvolging van gegevens verschijnt, dus om deze te verkrijgen is het noodzakelijk om de gegevens eerst te bestellen.

Als het aantal observaties vreemd is, is er geen probleem bij het vinden van het middelpunt van de set, maar als we een paar gegevens hebben, worden de twee centrale gegevens gevraagd en gemiddeld.

-Mode Het is de meest voorkomende waarde die wordt waargenomen in de gegevensset. Het bestaat niet altijd, omdat het mogelijk is dat geen waarde vaker wordt herhaald dan een andere. Er kunnen ook twee gegevens met gelijke frequentie zijn, in welk geval er sprake is van een bi-modale verdeling.

In tegenstelling tot de vorige twee maatregelen kan mode worden gebruikt met kwalitatieve gegevens.

Laten we eens kijken hoe deze positiemaatregelen worden berekend met een voorbeeld:

Opgelost voorbeeld

Stel dat u het rekenkundige gemiddelde, de mediaan en de mode wilt bepalen in het in het begin voorgestelde voorbeeld: de leeftijd van 20 werknemers van een cafetaria:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

De half Het wordt eenvoudig berekend door alle waarden toe te voegen en te delen door n = 20, wat het totale aantal gegevens is. Op deze manier:

Kan u van dienst zijn: evenredigheidsrelaties: concept, voorbeelden en oefeningen

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 jaar.

Om de mediaan Het is noodzakelijk om de gegevensset eerst te bestellen:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Zoals een paar gegevens zijn, worden de twee centrale gegevens, die vetgedrukt worden gemarkeerd en gemiddeld worden genomen en gemiddeld. Omdat beide 22 zijn, is de mediaan 22 jaar.

eindelijk, de mode Het is het feit dat het meest wordt herhaald of dat wiens frequentie groter is, zijnde deze 22 jaar.

Bereik, variantie, standaardafwijking en bias

Het bereik is gewoon het verschil tussen de belangrijkste en de minste van de gegevens en maakt het mogelijk om hun variabiliteit snel te waarderen. Maar afgezien zijn er andere dispersiemaatregelen die meer informatie bieden over gegevensverdeling.

Variantie en standaardafwijking

De variantie wordt aangeduid als s en wordt berekend door expressie:

Het wordt vaak bewerkt met de quasiriance in plaats van de variantie, die op dezelfde manier wordt berekend, alleen gedeeld door N-1, in plaats van te doen tussen n:

Aangezien de variantie de som van vierkanten is, resulteert in het kwadraat van de monstereenheid. In de studie van de leeftijd van werknemers in de cafetaria zou de variantie bijvoorbeeld in jaren komen².

Vervolgens om de resultaten terecht te interpreteren, wordt de standaardafwijking zoals de vierkantswortel van de variantie, of ook de standaard quasi-deviatie gedefinieerd, die de vierkantswortel van de quasivariantie is:

Vooroordeel

Het is de vergelijking tussen de gemiddelde X en de mediaan Med:

-Ja med = media x: de gegevens zijn symmetrisch.

-Wanneer x> med: bevooroordeeld aan de rechterkant.

-En als x < Med: los datos sesgan hacia la izquierda.

Oefening opgelost

Zoek gemiddeld, mediaan, mode, rang, variantie, standaardafwijking en vooringenomenheid voor de resultaten van een intellectueel coëfficiëntonderzoek van 20 studenten van een universiteit:

Kan u van dienst zijn: wiskundige functies

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Oplossing

We zullen de gegevens bestellen, omdat het nodig is om de mediaan te vinden.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

En we zullen ze als volgt in een tafel plaatsen, om de berekeningen te vergemakkelijken. De tweede kolom getiteld "Accumulated" is de som van de overeenkomstige gegevens plus de vorige.

Deze kolom vindt gemakkelijk het gemiddelde, waarbij de laatste wordt opgebouwd tussen het totale aantal gegevens, zoals te zien aan het einde van de "geaccumuleerde" kolom:

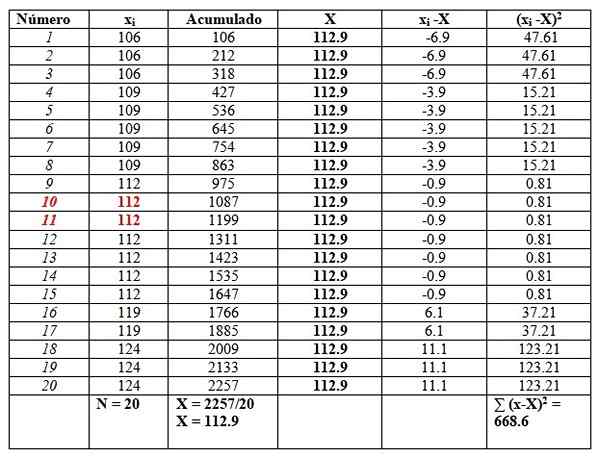
X = 112.9

De mediaan is het gemiddelde van de centrale gegevens gemarkeerd in rood: nummer 10 en nummer 11. Net als hetzelfde is de mediaan 112.

Ten slotte is mode de waarde die het meest wordt herhaald en 112 is, met 7 herhalingen.

Wat betreft dispersiemaatregelen, het bereik is:

124-106 = 18.

De variantie wordt verkregen door het uiteindelijke resultaat van de rechter kolom te delen tussen n:

S = 668.6/20 = 33.42

In dit geval is de standaardafwijking de vierkantswortel van de variantie: √33.42 = 5.8.

Aan de andere kant zijn de waarden van de quasivariarness en de Quasi Standard Deviation:

S_C= 668.6/19 = 35.2

Standaard quasi-deviatie = √35.2 = 5.9

Ten slotte is Bias enigszins rechts, omdat het gemiddelde 112.9 is groter dan de mediaan 112.

Referenties

1. Berenson, m. 1985. Statistieken voor administratie en economie. Inter -American S.NAAR.
2. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
3. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
4. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
5. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.