Curtosis definitie, typen, formules, waarvoor bijvoorbeeld

De Curtosis of kurtosis Het is een statistische parameter die dient om de kansverdeling van een willekeurige variabele te karakteriseren, wat de concentratie van waarden rond de centrale maat aangeeft. Dit staat ook bekend als "Peak Grade".

De term komt van de Griekse "kurtos", wat gebogen betekent, daarom geeft de Curtosis de mate van wijzen of afvlakken van de verdeling aan, zoals te zien in de volgende figuur:

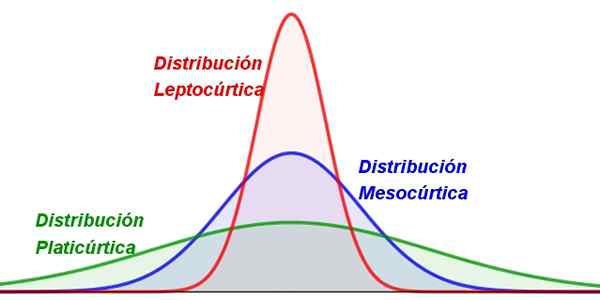Figuur 1. Verschillende soorten Curtosis. Bron: f. Zapata.

Bijna alle waarden van een willekeurige variabele hebben de neiging om rond een centrale waarde te groeperen, zoals gemiddeld. Maar in sommige distributies zijn de waarden meer verspreid dan in andere, wat resulteert in meer afgeplatte of meer slanke curven.

[TOC]

Definitie

Curtosis is een numerieke waarde van elke frequentieverdeling, die volgens de concentratie van waarden rond het gemiddelde wordt ingedeeld in drie groepen:

-Leptocuric: waarin de waarden erg gegroepeerd zijn rond het gemiddelde, dus de verdeling is behoorlijk puntig en slank (figuur 1, links).

-Mesocuric: Het heeft een matige concentratie waarden rond gemiddeld (figuur 1 in het midden).

-Phylicuric: Deze verdeling heeft een bredere vorm, omdat de waarden meestal meer verspreid zijn (figuur 1 aan de rechterkant).

Formules en vergelijkingen

Curtosis kan enige waarde hebben, zonder beperkingen. De berekening ervan wordt uitgevoerd, afhankelijk van de manier waarop de gegevens worden geleverd. De in elk geval gebruikte notatie is als volgt:

-Cortose -coëfficiënt: G₂

-Rekenkundig gemiddelde: X of X met bar

-Een i -eme: X_Je

-De standaardafwijking: σ

-Het aantal gegevens: N

-De frequentie van de i-esimo: F_Je

-Klasmerk: MX_Je

Met deze notatie presenteren we enkele van de meest gebruikte formules om Curtosis te vinden:

Kan u van dienst zijn: Vector Space: Base en Dimension, Axioms, Properties

- Curtosis volgens de presentatie van de gegevens

Zonder te groeperen of gegroepeerde gegevens bij frequenties

Gegevens gegroepeerd met intervallen

Overtollig van Curtosis

Ook wel genoemd Fisher's wijzende coëfficiënt of Fisher -maatregel, Het dient om de verdeling te vergelijken met normale verdeling.

Wanneer overtollige Curtosis 0 waard is, zijn we in aanwezigheid van een normale verdeling of Gauss Bell. Op deze manier, zolang de overtollige bruinen van een verdeling wordt berekend, vergelijken we deze eigenlijk met de normale verdeling.

Zowel voor de gegevens zonder groepering als voor de gegroepeerde gegevens, is de Fisher -wijscoëfficiënt, aangeduid door K,:

K = G₂ - 3

Er kan echter worden aangetoond dat de curtose van de normale verdeling 3 is, daarom als de wijs van de visser 0 of bijna 0 is en er een mesocurische verdeling is. Als k> 0 is de verdeling leptocurisch en als k<0 es platicúrtica.

Waar is Curtosis voor?

Curtosis is een maat voor variabiliteit die wordt gebruikt om de morfologie van een verdeling te karakteriseren. Op deze manier kunnen symmetrische verdelingen worden vergeleken met hetzelfde gemiddelde en gelijke dispersie (gegeven door de standaardafwijking).

Het hebben van variabiliteitsmaatregelen zorgt ervoor dat de gemiddelden betrouwbaar zijn en helpt bij het regelen van distributievariaties. Laten we bijvoorbeeld deze twee situaties analyseren.

3 afdelingen salarissen

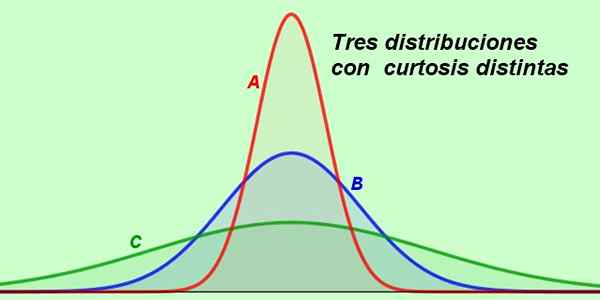
Stel dat de volgende grafiek de distributies toont in het salaris van 3 afdelingen van hetzelfde bedrijf:

Figuur 2. Drie verschillende distributies illustreren praktische situaties. (Bereid door Fanny Zapata)

Curve A is de meest slanke van allemaal, en in zijn vorm wordt afgeleid dat de meeste salarissen van die afdeling zeer dicht bij het gemiddelde zijn, daarom ontvangen de meeste werknemers een vergelijkbare compensatie.

Kan u van dienst zijn: hele nummers

Van zijn aandeel in afdeling B volgt de salariscurve een normale verdeling, omdat de curve mesocurisch is, waarin we aannemen dat salarissen willekeurig zijn verdeeld.

En ten slotte hebben we de C -curve die erg afgeplat is, een teken dat in deze afdeling het salarisbereik veel breder is dan in de andere.

De resultaten van een examen

Stel nu dat de drie curven van figuur 2 de resultaten vertegenwoordigen van een examen dat wordt toegepast op drie groepen studenten van hetzelfde onderwerp.

De groep wiens kwalificaties door de curve tot Leptocuric worden weergegeven, is vrij homogeen, het meest verkregen een gemiddelde of nauwe beoordeling.

Het is ook mogelijk dat het resultaat te wijten was aan het feit dat de examenvragen min of meer dezelfde moeilijkheid hadden.

Aan de andere kant duiden de resultaten van groep C aan een grotere heterogeniteit in de groep, die waarschijnlijk gemiddelde studenten bevat, sommige meer uitstekende studenten en zeker nog een minder attent.

Of het kan betekenen dat de vragen van de test heel verschillende moeilijkheden hadden.

Curve B is mesocurisch en geeft aan dat de testresultaten een normale verdeling volgden. Dit is meestal het meest voorkomende geval.

Opgelost voorbeeld van Curtosis

Vind Fisher's wijzende coëfficiënt voor de volgende cijfers, verkregen in een fysica -examen aan een groep studenten, met een schaal van 1 tot 10:

5, 5, 4, 7, 7.7, 9, 8, 9, 4, 3

Oplossing

De volgende expressie wordt gebruikt voor niet -groepen gegevens, gegeven in de voorgaande secties:

Met de Fisher Point -coëfficiënt gegeven door:

Kan u van dienst zijn: Pythagorische identiteiten: demonstratie, bijvoorbeeld oefeningen

K = G₂ - 3

Met deze waarde kan het type verdeling weten.

Om G te berekenen₂ Het is handig om dit op een ordelijke manier te doen, stap voor stap, omdat verschillende rekenkundige bewerkingen moeten worden opgelost.

Stap 1

Ten eerste wordt het gemiddelde van de kwalificaties berekend. Er zijn n = 11 gegevens.

X = (5+5+4+7+7+7+7+9+8+9+4+3)/11 = 6.182

Stap 2

De standaardafwijking wordt gevonden, waarvoor deze vergelijking wordt gebruikt:

 Door een rekenmachine met statistische functies te gebruiken, is het resultaat onmiddellijk:

σ = 1.992

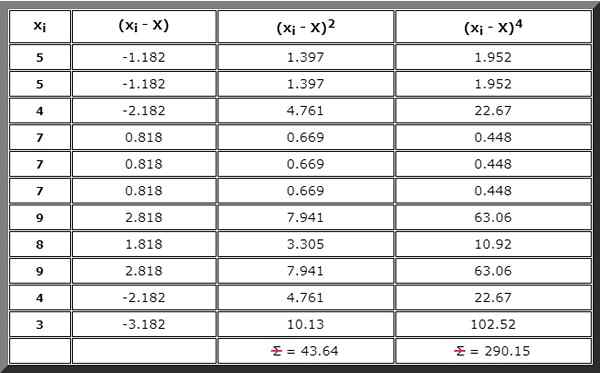
Of u kunt ook een tabel bouwen, die ook vereist is voor de volgende stap en waarin elke term van de samenvattingen die nodig zijn, wordt geschreven, beginnend met (x_Je - X), dan (x_Je - X)² En dan (x_Je - X)⁴ :

Stap 3

Voer de som uit die wordt aangegeven in de formuleteller voor G₂. Hiervoor wordt het resultaat van de rechter kolom van de vorige tabel gebruikt:

∑ (X_Je - X)⁴= 290.vijftien

Daarom:

G₂ = (1/11) x 290.15/1 1.992⁴ = 1.675

Fisher's bewegwijzeringcoëfficiënt is:

K = G₂ - 3 = 1.675 - 3 = -1.325

Welke belangen is het teken van het resultaat, dat, indien negatief, overeenkomt met een platitud van verschillende niveaus van moeilijkheden.

Het gebruik van een spreadsheet zoals Excel, vergemakkelijkt de resolutie van dit soort problemen aanzienlijk en biedt ook de optie om de distributie in te leiden.

Referenties

1. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
2. Marco, f. Curtosis. Hersteld van: economipedia.com.
3. Oliva, J. Asymmetrie en Curtosis. Opgehaald uit: StatisticsAucv.Bestanden.WordPress.com.
4. Spurr, w. 1982. Besluitvorming bij administratie. Limusa.
5. Wikipedia. Kurtosis. Opgehaald uit: in.Wikipedia.borg.