Definitie van onmiddellijke snelheid, formule, berekening en oefeningen

De onmiddellijke snelheid Het wordt gedefinieerd als de onmiddellijke verandering van verplaatsing in de loop van de tijd. Het is een concept dat grote precisie toevoegt aan de studie van beweging. En het is een vooruitgang met betrekking tot de gemiddelde snelheid, wiens informatie erg algemeen is.

Laten we eens kijken naar een tijdsinterval zo klein mogelijk om onmiddellijke snelheid te verkrijgen. Differentiële calculus is het perfecte hulpmiddel om dit idee wiskundig uit te drukken.

Onmiddellijke snelheid is verantwoordelijk voor mobiele snelheid op elk punt van de route. Bron: Pixabay.

Het startpunt is de gemiddelde snelheid:

Laten we nu AT AT -benadering maken van 0 alles wat kan. Dit is een limiet en het resultaat zal precies de onmiddellijke snelheid zijn:

Deze limiet is bekend onder de naam van afgeleide. In de notatie van differentiële calculus heb je:

Op voorwaarde dat de beweging beperkt is tot een rechte lijn, kan deze worden afgegeven met de vectornotatie.

[TOC]

Instantsnelheidberekening: geometrische interpretatie

De volgende figuur toont de geometrische interpretatie van het concept van derivaat: het is de helling van de lijn raaklijn Naar de curve x (t) vs. T Op elk punt.

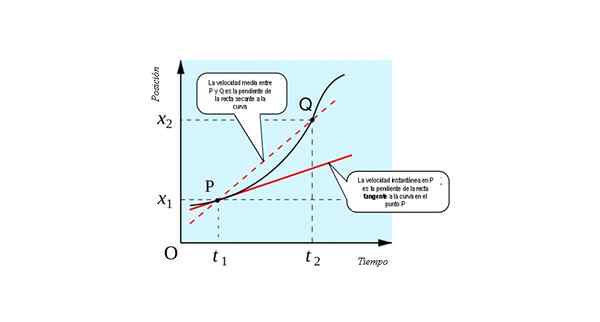De momentane snelheid in p equivalent numeriek tot de helling van de lijn raakt naar de curve x vs. t op punt P. Bron: Bron: すじにく シチュー シチュー [CC0].

U kunt zich voorstellen hoe u de limiet kunt verkrijgen als het punt Q geleidelijk nadert. Er zal een tijd komen dat beide punten zo dichtbij zijn, dat de ene niet van de andere kan worden onderscheiden.

De lijn die ze verenigt, zal dan drogen (recht dat in twee punten snijdt) om te rangen (recht die de curve op een enkel punt raakt). Daarom, om de onmiddellijke snelheid van een mobiel deeltje te vinden dat we zouden moeten hebben:

• De grafiek van de positie van het deeltje als een functie van de tijd. Het vinden van de helling van de lijn die op elk moment van de curve raakt, heb je de onmiddellijke snelheid op elk punt bezet door het deeltje.

Kan u van dienst zijn: Ampère Law: Formule and Vergelijkingen, Demonstratie, Oefeningen

O goed:

• De deeltjespositiefunctie x (t), die is afgeleid om de snelheidsfunctie te verkrijgen V (t), dan wordt deze functie op elk moment geëvalueerd T, Een gemak. De positiefunctie zou moeten worden afgeleid.

Enkele speciale gevallen bij de berekening van onmiddellijke snelheid

-De helling van de lijn raakt de curve in P is 0. Een nulhelling betekent dat de mobiel wordt gestopt en dat zijn snelheid natuurlijk 0 is.

-De helling van de lijn raakt de curve in P is groter dan 0. De snelheid is positief. In de bovenstaande grafiek betekent dit dat de mobiel weggaat van of.

-De helling van de lijn raakt de curve in P is minder dan 0. De snelheid zou negatief zijn. In de bovenstaande grafiek zijn er geen dergelijke punten, maar in dat geval zou het deeltje naderen of.

-De helling van de lijn die op de curve raakt, is constant in P en alle andere punten. In dit geval is de grafiek een rechte lijn en de mobiel heeft uniforme lijnbeweging MRU (zijn snelheid is constant).

Over het algemeen, de functie V (t) Het is ook een tijdfunctie, die op zijn beurt kan zijn afgeleid. Wat als het niet mogelijk was om die afkomstig te vinden van de functies x (t) En V (t)?

In het geval van x (t) Het kan zijn dat de helling - de momentane snelheid - scherp veranderde. Of dat gaat onmiddellijk van nul naar een andere waarde.

Zo ja, de afbeeldingen x (t) Het zou tips of hoeken presenteren bij de plotselinge veranderingen. Heel anders dan de casus weergegeven in de vorige afbeelding, waarin de curve x (t) Het is een zachte curve, zonder punten, hoeken, discontinuïteiten of abrupte veranderingen.

Kan u van dienst zijn: Bose Einstein Condensaat

De waarheid is dat voor echte mobiele telefoons zachte curven degenen zijn die het gedrag het beste vertegenwoordigen van het object.

De algemene beweging is vrij complex. Mobile kan een tijdje worden gestopt, versnellen om van de rust te gaan om een ​​snelheid te hebben en weg te komen van het startpunt, een tijdje snelheid te houden en dan te stoppen om opnieuw te stoppen en dus de stijl.

Ze kunnen opnieuw beginnen en in dezelfde richting doorgaan. Of handel de tegenslag en keer terug. Dit wordt een gevarieerde beweging genoemd in een dimensie.

Onder enkele voorbeelden van de berekening van onmiddellijke snelheid zullen het gebruik van de gegeven definities verduidelijken:

Opgeloste onmiddellijke snelheidsoefeningen

Oefening 1

Een deeltje beweegt langs een rechte lijn met de volgende bewegingswetgeving:

x (t) = -t³ + 2 t² + 6 T - 10

Alle eenheden zijn in het internationale systeem. Vinden:

a) De positie van het deeltje op t = 3 seconden.

b) De gemiddelde snelheid in het interval tussen t = 0 s en t = 3 s.

c) De gemiddelde snelheid in het interval tussen t = 0 s en t = 3 s.

d) De momentane snelheid van het deeltje van de vorige vraag, op t = 1 s.

Antwoorden

a) Om de positie van het deeltje te vinden, de bewegingswet (positiefunctie) op t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Er is geen probleem dat de positie negatief is. Het teken (-) geeft aan dat het deeltje links van de oorsprong is of.

b) Bij de berekening van de gemiddelde snelheid zijn de uiteindelijke en beginposities van het deeltje vereist in de aangegeven tijden: x (3) en x (0). De positie op t = 3 is x (3) en is bekend over het vorige resultaat. De positie op t = 0 seconden is x (0) = -10 m.

Kan u van dienst zijn: statisch: geschiedenis, welke studies, toepassingen, wetten

Omdat de uiteindelijke positie hetzelfde is als de eerste, wordt onmiddellijk geconcludeerd dat de gemiddelde snelheid 0 is.

c) De gemiddelde snelheid is de reden tussen de afgelegde afstand en de tijd die wordt besteed. Nu is de afstand de module of grootte van de verplaatsing, daarom:

Afstand = | x2 - x1 | = | -10-(-10) | M = 20 m

Merk op dat de afgelegde afstand altijd positief is.

v_{m = 20 m/3 s = 6.7 m/s}

d) Hier is het noodzakelijk om de eerste afgeleide van de positie met betrekking tot de tijd te vinden. Dan wordt het geëvalueerd voor t = 1 seconde.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Oefening 2

Hieronder is de grafiek van de positie van een mobiel als functie van de tijd. Zoek de momentane snelheid op t = 2 seconden.

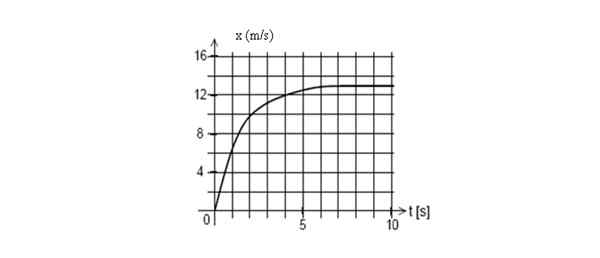Positiegrafiek versus tijd voor een mobiel. Bron: zelf gemaakt.

Antwoord

Trek de raaklijn op de curve op t = 2 seconden, bereken vervolgens uw helling en neem twee punten van de lijn.

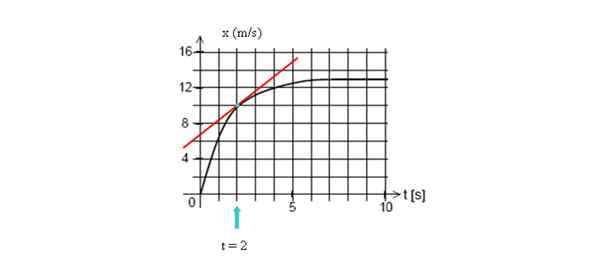Om de momentane snelheid op het aangegeven punt te berekenen, trekt u de raaklijn naar dat punt en vindt u de helling. Bron: zelf gemaakt.

In dit voorbeeld zullen we twee punten nemen die gemakkelijk worden gevisualiseerd, waarvan de coördinaten (2 s, 10 m) zijn en de snit met de verticale as (0 s, 7 m):

Referenties

1. Giancoli, D. Natuurkunde. Principes met toepassingen. 6^e Editie. Prentice Hall. 22-25.
2. Resnick, r. (1999). Fysiek. Deel 1. Derde editie in het Spaans. Mexico. Continental Editorial Company s.NAAR. van C.V. 21-22.
3. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7^ma. Editie. Mexico. Cengage Learning Editors. 23-25.