Normale berekening en voorbeeldvector

Hij Normale vector Het is er een die de richting definieert die loodrecht op een geometrische entiteit wordt overwogen, die kan zijn voor een curve, een vlak of een oppervlak, bijvoorbeeld.

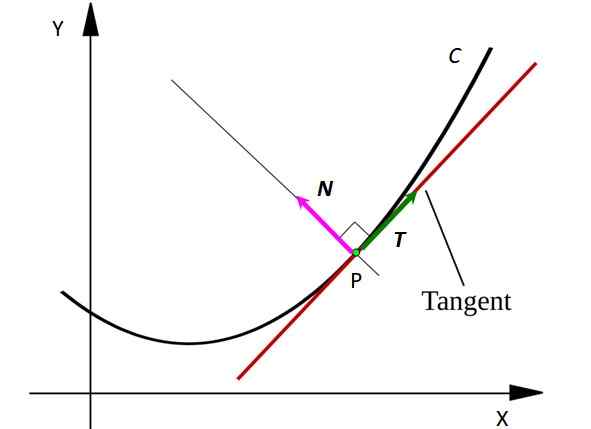
Het is een zeer nuttig concept bij de positionering van een mobiel deeltje of een oppervlakte in de ruimte. In de volgende grafiek is het mogelijk om te zien hoe de normale vector is voor een willekeurige curve C:

Figuur 1. Een C -curve met de normale vector naar de curve op punt P. Bron: SVJO [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)]

Overweeg een punt P op curve c. Het punt kan een mobiel deeltje vertegenwoordigen dat beweegt na een C -vormige weg. De lijn raakt naar de curve op punt P verschijnt in rood getekend.

Merk op dat de vector T Het is op elk punt rangen door C, terwijl de vector N staat loodrecht op T en wijst naar het midden van een denkbeeldige omtrek waarvan de boog een segment van C is. Vectoren worden in gedurfde letter in gedrukte tekst aangeduid om ze te onderscheiden van andere niet -vectorgroottes.

De vector T Het geeft altijd aan waar het deeltje beweegt, daarom geeft het de snelheid van hetzelfde aan. In plaats daarvan de vector N Wijs altijd in de richting waarin het deeltje draait, op deze manier duidt het op de concaafheid van de C -curve.

[TOC]

Hoe u de normale vector in een vlak kunt krijgen?

De normale vector is niet noodzakelijk een eenheidsvector, dat wil zeggen een vector waarvan de module 1 is, maar als dat zo is, wordt deze genoemd Normale eenheidsvector.

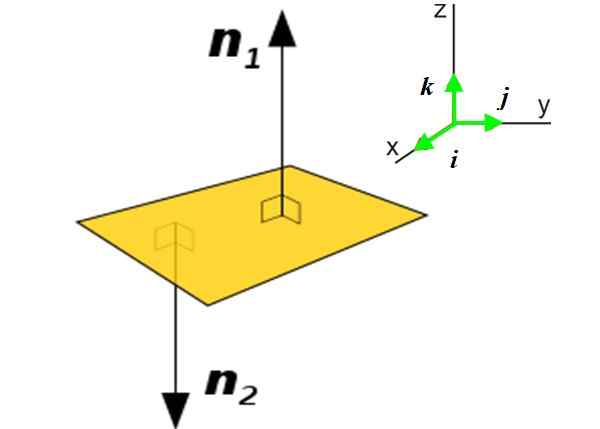
Figuur 2. Links een P -vlak en de twee normale vectoren naar het genoemde vlak. Aan de rechterkant de eenheidsvectoren in de drie richtingen die de ruimte bepalen. Bron: Wikimedia Commons. Zie pagina voor auteur [Public Domain]

In talloze toepassingen is het noodzakelijk om de normale vector in een vlak te kennen in plaats van een curve. Deze vector maakt bekend de oriëntatie van het genoemde vlak in de ruimte. Overweeg bijvoorbeeld het vliegtuig P (geel) van de figuur:

Het kan u van dienst zijn: Gemine: oorsprong, kenmerken en hoe u deze kunt observeren

Er zijn twee normale vectoren in dat vlak: N₁ En N₂. Het gebruik van het een of het ander zal afhangen van de context waarin dit vlak wordt gevonden. Het verkrijgen van de normale vector in een vlak is heel eenvoudig als de vergelijking ervan bekend is:

Ax + door + CZ + D = 0, met naar, B, C En D echte getallen.

Nou, een normale vlakvector wordt gegeven door:

N = A Je + B J + C k

Hier de vector N wordt uitgedrukt in termen van de eenheidsvectoren en loodrecht op elkaar Je, J En k, Gericht over de drie richtingen die de ruimte bepalen X en Z, Zie figuur 2 goed.

De normale vector van het vectorproduct

Een zeer eenvoudige procedure om de normale vector te vinden maakt gebruik van de eigenschappen van het vectorproduct tussen twee vectoren.

Zoals bekend, bepalen drie verschillende punten en niet colineal met elkaar, een P -vlak. Nu is het mogelijk om twee vectoren te verkrijgen of En v die behoren tot het genoemde vliegtuig met deze drie punten.

Zodra de vectoren zijn, de Vectorproduct of X v Het is een bewerking waarvan het resultaat een vector is, die de eigenschap heeft om loodrecht op het vlak te zijn bepaald door of En v.

Bekend deze vector, wordt het aangeduid als N, En daaruit zal het mogelijk zijn om de vergelijking van het vlak te bepalen dankzij de vergelijking die wordt aangegeven in de voorgaande sectie:

N = of X v

De volgende figuur illustreert de beschreven procedure:

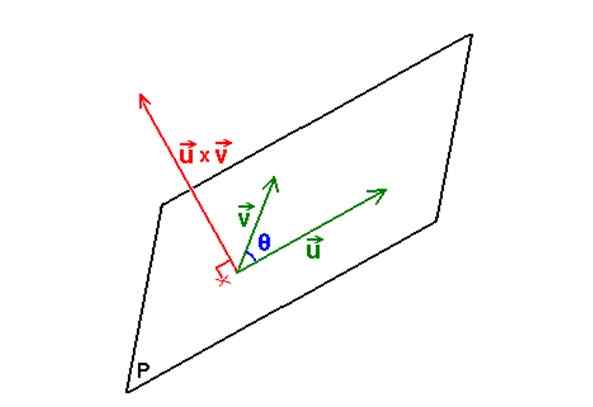figuur 3. Met twee vectoren en hun vector of kruisproduct wordt de vergelijking van het vlak dat de twee vectoren bevat, bepaald. Bron: Wikimedia Commons. Geen machine-leesbare auteur verstrekt. M.Romero Schmidtke nam aan (op basis van copyrightclaims). [Publiek domein]

Voorbeeld

Zoek de vergelijking van het vlak bepaald door punten A (2,1,3); B (0,1,1); C (4,2,1).

Kan u van dienst zijn: continuïteitsvergelijking

Oplossing

Deze oefening illustreert de hierboven beschreven procedure. Door 3 punten te hebben, wordt een van hen gekozen als een gemeenschappelijke oorsprong van twee vectoren die tot het vlak zijn gedefinieerd door deze punten. Punt A is bijvoorbeeld ingesteld als oorsprong en vectoren worden gebouwd Aab En AC.

De vector Aab Het is de vector waarvan de oorsprong punt A is en waarvan het einde punt B is. Vector's coördinaten Aab De coördinaten van B van de coördinaten van A:

Aab = (0-2) Je + (1-1) J + (1-3) k = -2Je + 0J -2 k

Ga op dezelfde manier verder om de vector te vinden AC:

AC = (4-2) Je + (2-1) J + (1-3) k = 2Je + J -2 k

Vectorproductberekening AB X AC

Er zijn verschillende procedures om het vectorproduct tussen twee vectoren te vinden. In dit voorbeeld wordt een mnemonische procedure gebruikt die gebruik maakt van de volgende figuur om vectorproducten te vinden tussen eenheidsvectoren Je, J En K:

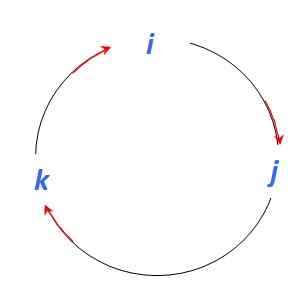Figuur 4. Grafisch om het vectorproduct tussen de eenheidsvectoren te bepalen. Bron: zelf gemaakt.

Om te beginnen is het goed om te onthouden dat vectorproducten tussen parallelle vectoren daarom nietig zijn:

Je X Je = 0; J X J = 0; k X k = 0

En omdat het vectorproduct een andere vector loodrecht op de deelnemende vectoren is, bewegend in de richting van de rode pijl:

Je X J = k ; J X k = Je; k X Je = J

Als u in strijd met de pijl moet bewegen, wordt een teken (-) toegevoegd:

J X Je = - k; k X J = -Je; Je X k = -J

In totaal is het mogelijk om 9 vectorproducten te maken met de eenheidsvectoren Je, J En k, waarvan 3 ongeldig zullen zijn.

Aab X AC = (-2Je + 0J -2 k) X (2Je + J -2 k) = -4 (Je X Je) -2 (Je X J) +4 (Je X k) +0 (J X Je) + 0 (J X J) - 0 (J X k) - 4 (k X Je) -2 (k X J) + 4 (k X k) = -2k-4J-4J+2Je = 2Je -8J-2k

Vliegtuigvergelijking

Vector N is bepaald door het eerder berekende vectorproduct:

Kan u van dienst zijn: Pendular Movement

N = 2Je -8J-2k

Daarom is a = 2, b = -8, c = -2, het gezochte plan is:

Ax + door + cz + d = 0 → 2x-8y-2z + d = 0

De waarde van D. Dit is eenvoudig als de waarden van een van de punten A, B of C die beschikbaar zijn, worden vervangen in de vlakvergelijking. Bijvoorbeeld kiezen van C:

x = 4; y = 2; Z = 1

Is overgebleven:

2.4 - 8.2 - 2.1 + d = 0

-10 + d = 0

D = 10

Kortom, het gewenste vliegtuig is:

2x-8y-2z +10 = 0

De nieuwsgierige lezer kan vragen of hetzelfde resultaat zou zijn verkregen als in plaats van te doen Aab X AC Het zou zijn gekozen AC X Aab. Het antwoord is ja, het vlak bepaald door deze drie punten is uniek en heeft twee normale vectoren, zoals weergegeven in figuur 2.

Wat betreft het geselecteerde punt als de oorsprong van de vectoren, is er ook geen ongemak bij het kiezen van een van de andere twee.

Referenties

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB). 31-62.
2. Het normaal vinden van een vlak. Opgehaald uit: Web.ma.Utexas.Edu.
3. Larson, r. (1986). Berekening en analytische geometrie. MC Graw Hill. 616 - 647.
4. Lijnen en plannen in R 3. Hersteld van: wiskunde.Harvard.Edu.
5. Normale vector. Hersteld van Mathworld.Wolfraam.com.