Statistische variabelen

Wat zijn statistische variabelen?

De Statistische variabelen zijn kenmerken die mensen, dingen of plaatsen bezitten en die kunnen worden gemeten. Voorbeelden van vaak gebruikte variabelen zijn leeftijd, gewicht, lengte, geslacht, civiele status, academisch niveau, temperatuur, het aantal uren dat een gloeilamp en vele anderen en vele anderen meegaat.

Een van de doelstellingen van de wetenschap is weten hoe de variabelen van een systeem zich gedragen om voorspellingen te kunnen doen over het toekomstige gedrag ervan. Volgens zijn aard vereist elke variabele een specifieke behandeling om er maximale informatie uit te verkrijgen.

De hoeveelheid variabelen om te studeren is enorm, maar het zorgvuldig onderzoeken van de bovengenoemde groep, we merken onmiddellijk dat sommige numeriek kunnen worden uitgedrukt, terwijl anderen dat niet doen.

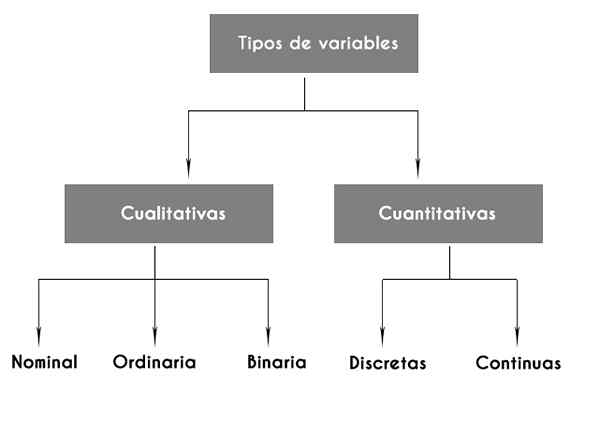
Dit geeft ons de eerste classificatie van de statistische variabelen in twee fundamentele typen: kwalitatief en numeriek.

Soorten statistische variabelen

- Kwalitatieve variabelen

Zoals de naam al aangeeft, worden kwalitatieve variabelen gebruikt om categorieën of kwaliteiten aan te duiden.

Een goed bekend voorbeeld van dit type variabelen is civiele status: alleenstaande, getrouwde, gescheiden of weduwnaar. Geen van deze categorieën is groter dan de andere, duidt alleen een andere situatie aan.

Meer variabelen van dit type zijn:

-Academisch niveau

-Jaar van het jaar

-Auto -merk dat wordt uitgevoerd

-Beroep

-Nationaliteit

-Landen, steden, districten, provincies en andere territoriale afdelingen.

Een categorie kan ook worden aangeduid met een nummer, bijvoorbeeld het telefoonnummer, het huisnummer, de straat of de postcode, zonder dat dit een numerieke beoordeling vertegenwoordigt, maar eerder een label.

Het straatnummer is een kwalitatieve variabele, het is geen kwantitatieve variabele

Nominale, ordinale en binaire variabelen

Kwalitatieve variabelen kunnen op hun beurt zijn:

-Nominaal, die een naam toewijzen aan de kwaliteit, zoals kleur bijvoorbeeld.

-Ordinals, die orde vertegenwoordigen, zoals in het geval van een schaal van sociaaleconomische lagen (hoog, gemiddeld, laag) of meningen over een soort voorstel (vóór, onverschillig, tegen). *

Kan u van dienst zijn: Gevrrees of Freedom: How To Bereken, Types, Voorbeelden

-Binair, Ook wel genoemd dichotomisch, Er zijn slechts twee mogelijke waarden, zoals seks. Aan deze variabele kan een numeriek label worden toegewezen, zoals 1 en 2, zonder een numerieke beoordeling of een soort orde weer te geven.

*Sommige auteurs nemen ordinale variabelen op in de groep kwantitatieve variabelen, die hieronder worden beschreven. Het is omdat ze de orde of hiërarchie uitdrukken.

- Numerieke of kwantitatieve variabelen

Deze variabelen krijgen een getal toegewezen, omdat ze bedragen vertegenwoordigen, zoals salaris, leeftijd, afstanden en kwalificaties verkregen in een examen.

Ze worden veel gebruikt om voorkeuren te contrasteren en trends te schatten. Ze kunnen worden geassocieerd met kwalitatieve variabelen en het bouwen van staven en histogrammenafbeeldingen die visuele analyse vergemakkelijken.

Sommige numerieke variabelen kunnen worden omgezet in kwalitatieve variabelen, maar het tegenovergestelde is niet mogelijk. De numerieke variabele "leeftijd" kan bijvoorbeeld worden onderverdeeld in intervallen met toegewezen labels, zoals baby's, kinderen, adolescenten, volwassenen en ouderen.

Er moet echter worden opgemerkt dat er bewerkingen zijn die kunnen worden gedaan met numerieke variabelen, die duidelijk niet kunnen worden uitgevoerd met kwalitatieve, bijvoorbeeld het berekenen van gemiddelden en andere statistische schatters.

Als u wilt berekenen, moet u de variabele "leeftijd" als een numerieke variabele behouden. Maar andere toepassingen vereisen mogelijk geen numerieke details, want deze zou voldoende zijn om de benoemde labels te laten.

Numerieke variabelen zijn op hun beurt verdeeld in twee hoofdcategorieën: afzonderlijke variabelen en continue variabelen.

Discrete variabelen

De discrete variabelen nemen alleen bepaalde waarden en worden gekenmerkt door boekhouding te zijn, bijvoorbeeld het aantal kinderen van een gezin, de hoeveelheid huisdieren, het aantal klanten dat dagelijks een winkel bezoekt en de abonnees van een kabelbedrijf, om te vermelden Een paar voorbeelden.

Kan u van dienst zijn: minimale vierkanten

Bijvoorbeeld het variabele "aantal huisdieren", neemt het zijn waarden van de reeks natuurlijke getallen in. Een persoon kan 0, 1, 2, 3 of meer huisdieren hebben, maar nooit 2.5 huisdieren bijvoorbeeld.

Een discrete variabele heeft echter noodzakelijkerwijs natuurlijke of gehele getallen. Decimale getallen dienen ook, omdat het criterium om te bepalen of een variabele discreet is, is dat dit boekhouding of genummerd is.

Stel bijvoorbeeld dat de fractie van defecte bollen wordt gedefinieerd als een variabele.

Als geen lamp defect is, neemt de variabele waarde 0 toe. Maar als 1 van N -lampen defect is, is de variabele 1 /n waard, als er twee defect is, is het 2 /n enzovoort totdat het bereiken van de gebeurtenis dat de N -lampen defect waren en in dat geval de fractie zou zijn 1.

Continue variabelen

In tegenstelling tot afzonderlijke variabelen kunnen continue variabelen elke waarde aannemen. Bijvoorbeeld het gewicht van studenten die een bepaald onderwerp, hoogte, temperatuur, tijd, lengte en vele andere bestuderen.

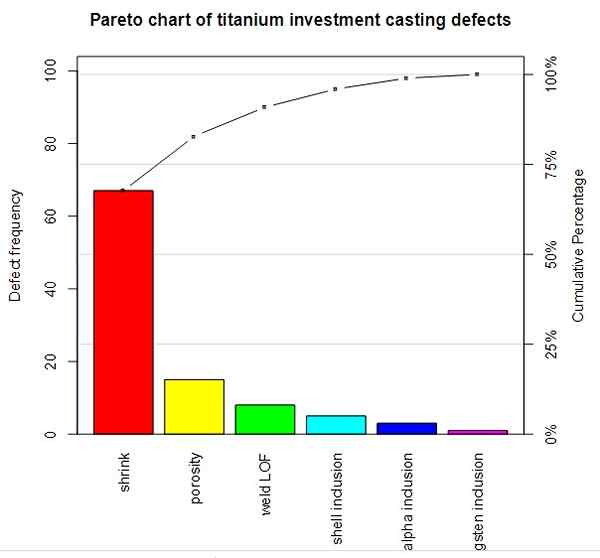Pareto -diagram Vergelijking van defectfrequentie (kwantitatieve variabele in de verticale as) en het cumulatieve percentage versus elk defect in de horizontale as (kwalitatieve variabele). Bron: Wikimedia Commons.

Omdat de continue variabele oneindige waarden nodig heeft, kunnen alle soorten berekeningen worden gemaakt met de gewenste precisie, alleen door het aantal decimalen aan te passen.

In de praktijk zijn er continue variabelen die kunnen worden uitgedrukt als afzonderlijke variabelen, bijvoorbeeld de leeftijd van een persoon.

De exacte leeftijd van een persoon kan worden geteld in jaren, maanden, weken, dagen en meer, afhankelijk van de gewenste precisie, maar meestal rondes in jaren en wordt dus discreet.

Het inkomen van een persoon is ook een continue variabele, maar het wordt meestal beter gewerkt als intervallen worden vastgesteld.

Kan u van dienst zijn: graad van een polynoom: hoe deze is bepaald, voorbeelden en oefeningen

- Afhankelijke en onafhankelijke variabelen

De afhankelijke variabelen zijn die gemeten tijdens een experiment, om de relatie te bestuderen die ze hebben met anderen, die als onafhankelijke variabelen zouden worden beschouwd.

voorbeeld 1

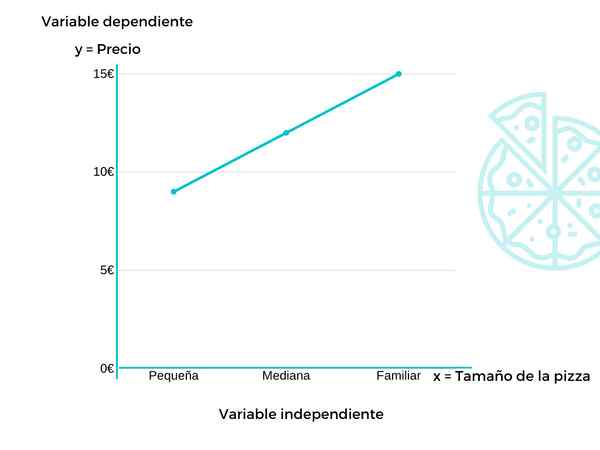
In dit voorbeeld zullen we de evolutie van prijzen zien die lijden aan de pizza's van een voedselplaats, afhankelijk van de grootte.

De afhankelijke variabele (y) zou de prijs zijn, terwijl de onafhankelijke variabele (x) de grootte zou zijn. In dit geval is de kleine pizza € 9 waard, de mediaan € 12 en de bekende € 15.

Dat wil zeggen, naarmate het pizzabaat toeneemt, kost het meer. Daarom zou de prijs afhankelijk zijn van de grootte.

Deze functie zou y = f (x) zijn

Voorbeeld 2

Een eenvoudig voorbeeld: u wilt het effect onderzoeken dat verandert in stroom die ik produceer door een metaaldraad, waarvoor de V -spanning wordt gemeten tussen de uiteinden hiervan.

De onafhankelijke variabele (de oorzaak) is de stroom, terwijl de afhankelijke variabele (het effect) de spanning is, waarvan de waarde afhangt van de stroom die door de draad reist.

In het experiment is wat wordt gezocht om te weten hoe de wet is als ik gevarieerd ben. Als de spanningsafhankelijkheid met de stroom lineair blijkt te zijn, dat wil zeggen: v ∝ i, de bestuurder is ohmisch en de constante van evenredigheid is de weerstand van draad.

Maar het feit dat een variabele onafhankelijk is in een experiment betekent niet dat deze in een ander zit. Dat hangt af van het te bestuderen fenomeen en het type onderzoek dat u wilt uitvoeren.

De stroom I die bijvoorbeeld een gesloten bestuurder reist die in een constant magnetisch veld draait, wordt de afhankelijke variabele ten opzichte van de tijd, die de onafhankelijke variabele zou worden.

Referenties

1. Berenson, m. 1985. Statistieken voor administratie en economie. Inter -American S.NAAR.
2. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
3. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
4. Economische encyclopedie. Continue variabelen. Hersteld van: encyclopediaeconomica.com.
5. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
6. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.