Wat is het statistische bereik? (Met voorbeelden)

Hij bereik, Tour of amplitude, in statistieken, is het verschil (aftrekken) tussen de maximale waarde en de minimale waarde van een set gegevens uit een steekproef of een populatie. Als het bereik met de letter R en de gegevens worden weergegeven door middel van X, De formule voor het bereik is eenvoudig:

R = x_maximaal - X_min

 Waar x_maximaal Het is de maximale waarde van de gegevens en x_min Het is het minimum.

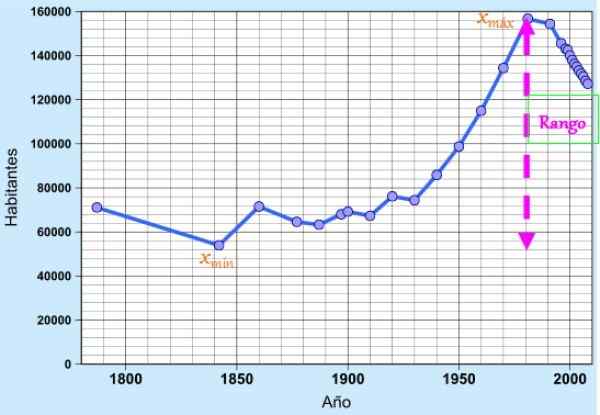
Figuur 1. Bereik van gegevens die overeenkomen met de populatie van Cádiz in de laatste twee eeuwen. Bron: Wikimedia Commons.

Het concept is zeer nuttig als een eenvoudige dispersiemaatregel om de variabiliteit van de gegevens snel te waarderen, omdat het de uitbreiding of de lengte van het interval aangeeft waar deze worden gevonden.

Stel bijvoorbeeld dat de status van een groep van 25 mannelijke studenten van het eerste jaar van engineering aan een universiteit. De hoogste student in de groep meet 1.93 m en de laagste 1.67 m. Dit zijn de extreme waarden van de steekproefgegevens, daarom is de route ervan:

R = 1.93 - 1.67 m = 0.26 m of 26 cm.

De status van de studenten van deze groep wordt in dit bereik gedistribueerd.

[TOC]

Voor-en nadelen

Het bereik is, zoals we eerder hebben gezegd, een maat voor hoe verspreid de gegevens zijn. Een klein bereik geeft aan dat de gegevens min of meer dichtbij zijn en dat de dispersie weinig is. Aan de andere kant is een groter bereik een indicatie dat de gegevens meer verspreid zijn.

De voordelen van het berekenen van het bereik zijn duidelijk: het is heel eenvoudig en snel om te vinden, omdat het een eenvoudig verschil is.

Het heeft ook dezelfde eenheden als de gegevens waarmee het werkt en het concept is heel gemakkelijk te interpreteren voor elke waarnemer.

In het voorbeeld van de status van technische studenten, als het bereik 5 cm was geweest, zouden we zeggen dat studenten allemaal van dezelfde grootte zijn. Maar met een bereik van 26 cm gaan we er onmiddellijk van uit dat er in de steekproef studenten van alle tussenliggende beelden zijn. Heeft deze veronderstelling altijd goed?

Het kan u van dienst zijn: verschil tussen cirkel en omtrek (met voorbeelden)

Nadelen van het bereik als een dispersiemaatregel

Als we goed kijken, in onze steekproef van 25 engineeringstudenten, meet slechts één van hen 1.93 en de resterende 24 hebben beelden van bijna 1.67 m.

En toch blijft het bereik hetzelfde, hoewel het perfect mogelijk is dat het tegenovergestelde optreedt: dat de gestalte van de meerderheid rond 1 oscilleert.90 m en slechts één meet 1.67 m.

In elk geval is de verdeling van de gegevens heel anders.

De nadelen van het bereik als een dispersiemaatregel zijn te wijten aan het feit dat het alleen extreme waarden gebruikt en alle andere negeert. Aangezien de meeste informatie verloren gaat, is er geen idee hoe de voorbeeldgegevens worden verdeeld.

Een ander belangrijk kenmerk is dat het bereik van het monster nooit afneemt. Als we meer informatie toevoegen, dat wil zeggen, we beschouwen meer gegevens, het bereik neemt toe of blijft hetzelfde.

En in elk geval is het alleen handig bij het werken met kleine monsters, het unieke gebruik wordt niet aanbevolen als een maat voor dispersie in grote monsters.

Wat moet worden gedaan, is om aan te vullen met de berekening van andere dispersiemaatregelen die rekening houden met de informatie die door de totale gegevens wordt verstrekt: route Onderlinge, Variantie, standaardafwijking en variatiecoëfficiënt.

Interquirile route, kwartielen en opgelost voorbeeld

We hebben ons gerealiseerd dat de zwakte van het bereik als een dispersiemaatregel is dat het alleen gebruik maakt van de extreme waarden van de verdeling van de gegevens, waardoor de anderen worden weggelaten.

Om dit ongemak te voorkomen, de kwartiel: drie waarden bekend als Positiemaatregelen.

Ze verdelen de gegevens die niet in vier delen zijn gegroepeerd (andere veelgebruikte positiemaatregelen zijn de Deciles en de percentiel)). Dit zijn de kenmerken:

-Het eerste kwartiel Q₁ Het is de waarde van de gegevens zodat 25 % van hen allemaal minder is dan Q₁.

Kan u van dienst zijn: evenredigheid Constant: wat is, berekening, oefeningen

-Het tweede kwartiel Q₂ Het is de mediaan van de verdeling, wat betekent dat de helft (50 %) van de gegevens minder is dan die waarde.

-Eindelijk het derde kwartiel Q₃ wijst erop dat 75 % van de gegevens minder zijn dan Q₃.

Vervolgens wordt het interquotielbereik of de interquartielroute gedefinieerd als het verschil tussen het derde kwartiel Q₃ en het eerste kwartiel Q₁ van de gegevens:

Interquotile Journey = R_Q = Q₃ - Q₁

Op deze manier is de waarde van de rang R_Q Het wordt niet zo beïnvloed door extreme waarden. Daarom is het raadzaam om het te gebruiken als het gaat om bevooroordeelde distributies, zoals zeer hoge of zeer lage studenten die hierboven zijn beschreven.

- Cuartyles -berekening

Er zijn verschillende manieren om ze te berekenen, hier zullen we er een voorstellen, maar in elk geval is het noodzakelijk om de Aantal bestelling "N_of”, Dat is de plaats die het respectieve kwartiel in de verdeling bezet.

Dat wil zeggen, als bijvoorbeeld de term die overeenkomt met Q₁ is de tweede, derde of vierde, enzovoort over de verdeling.

Eerste kwartiel

N_of (Q₁) = (N+1) / 4

Tweede kwartiel of mediaan

N_of (Q₂) = (N+1) / 2

Derde kwartiel

N_of (Q₃) = 3 (n+1) / 4

Waarbij n het gegevensnummer is.

De mediaan is de waarde die midden in de distributie zit. Als het gegevensnummer vreemd is, is er geen probleem om het te vinden, maar als het zelfs is, worden de twee centrale waarden gemiddeld om ze in één te veranderen.

Zodra het bestelnummer is berekend, wordt een van deze drie regels gevolgd:

-Als u geen decimalen heeft, worden de gegevens die in de verdeling worden aangegeven, en dit is de vierde gezochte door.

-Wanneer het bestelnummer halverwege twee is, zijn de gegevens die door het gehele onderdeel worden aangegeven met het volgende feit gemiddeld en het resultaat is het overeenkomstige kwartiel.

-In elk ander geval is het dichtstbijzijnde gehele getal afgerond en dat zal de vierde plaats zijn.

Kan u van dienst zijn: additief principe

Opgelost voorbeeld

Op een schaal van 0 tot 20, een groep van 16 wiskundestudenten, behaalde ik de volgende cijfers (punten) in een gedeeltelijk examen:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Vinden:

a) De gegevens- of gegevensroute.

b) De waarden van het kwartielen q₁ en Q₃

c) het tussenwijkbereik.

Figuur 2. Doet de kwalificaties van dit wiskunde -examen zoveel variabiliteit? Bron: Pixabay.

Oplossing voor

Het eerste wat u moet doen om de route te vinden, is om de gegevens te bestellen die toenemen of afnemen. Bijvoorbeeld in toenemende volgorde die u hebt:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Door de formule die in het begin wordt gegeven: r = x_maximaal - X_min

R = 20 - 1 punten = 19 punten.

Volgens het resultaat hebben deze cijfers een grote verspreiding.

Oplossing B

N = 16

N_of (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

Het is een nummer met decimalen, waarvan het hele deel 4 is. Dan gaan we naar de verdeling, de gegevens die de vierde plaats innemen, worden gezocht en de waarde ervan wordt gemiddeld met die van de vijfde positie. Omdat beide 9 zijn, is het gemiddelde ook 9 en dan:

Q₁ = 9

Nu herhalen we de procedure om Q te vinden₃:

N_of (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Nogmaals, het is een decimaal, maar omdat het niet halverwege is, is het afgerond op 13. Het gezochte kwartiel neemt de dertien positie in en is:

Q₃ = 16

Oplossing C

R_Q = Q₃ - Q₁ = 16 - 9 = 7 punten.

Dat zoals we zien is veel minder dan het gegevensbereik berekend in sectie A), omdat de minimale beoordeling 1 punt was, een waarde veel verder van de rest.

Referenties

1. Berenson, m. 1985. Statistieken voor administratie en economie. Inter -American S.NAAR.
2. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
3. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
4. Voorbeelden van kwartielen. Opgehaald uit: Mathematics10.netto.
5. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
6. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.