Vrijheidsgraden Hoe deze te berekenen, typen, voorbeelden

De graden van vrijheid In statistieken zijn het aantal onafhankelijke componenten van een willekeurige vector. Als de vector heeft N componenten en dat zijn er P lineaire vergelijkingen die zijn componenten relateren, vervolgens de graad van vrijheid Het is n-p.

Het concept van graden van vrijheid Het verschijnt ook in theoretische mechanica, waar ze in een grove modus gelijkwaardig zijn aan de dimensie van de ruimte waar het deeltje beweegt, behalve het aantal ligaturen.

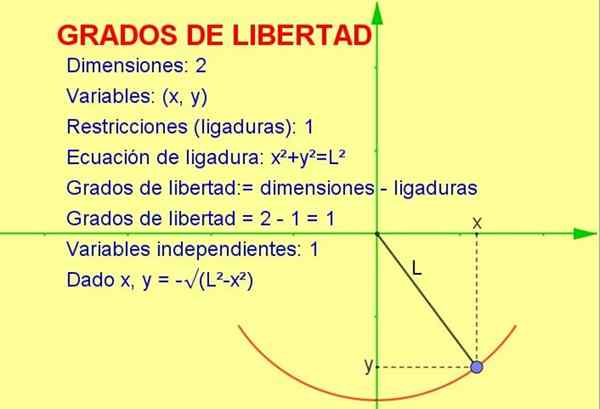
Figuur 1. Een slinger beweegt in twee dimensies, maar het heeft slechts een zekere vrijheid omdat het verplicht is om in een straal te bewegen. Bron: f. Zapata.

Dit artikel bespreekt het concept van vrijheidsgraden die op statistieken worden toegepast, maar een mechanisch voorbeeld is gemakkelijker te visualiseren op een geometrische manier.

[TOC]

Soorten vrijheidsgraden

Volgens de context waarin het wordt toegepast, kan de manier om het aantal vrijheidsgraden te berekenen variëren, maar het onderliggende idee is altijd hetzelfde: totale dimensies Minder aantal beperkingen.

In een mechanisch geval

Overweeg een deeltje dat oscilleert gebonden aan een touw (een slinger) dat beweegt in het verticale vlak X-Y (2 dimensies). Het deeltje is echter verplicht om op de straalomtrek te bewegen gelijk aan de lengte van het touw.

Omdat het deeltje alleen maar op die curve kan bewegen, het aantal graden van vrijheid Het is 1. Dit kan worden gevisualiseerd in figuur 1.

De manier om het aantal vrijheidsgraden te berekenen, is om het verschil te maken in het aantal dimensies behalve het aantal beperkingen:

Vrijheidsgraden: = 2 (dimensies) - 1 (ligatie) = 1

Een andere verklaring waarmee we het resultaat kunnen bereiken, is als volgt:

-We weten dat de twee -dimensionale positie wordt weergegeven door een coördinaatpunt (x, y).

-Maar omdat het punt de omtrekvergelijking moet vervullen (x² + En² = L²) Voor een gegeven waarde van variabele X, de variabele en wordt bepaald door genoemde vergelijking of beperking.

Op deze manier is slechts één van de variabelen onafhankelijk en het systeem heeft Eén (1) vrijheidsgraad.

Kan u van dienst zijn: klassieke waarschijnlijkheid: berekening, voorbeelden, opgeloste oefeningen

In een reeks willekeurige waarden

Om te illustreren wat het concept betekent dat de vector

X = (x₁, X₂,…, X_N))

Het vertegenwoordigen van de steekproef van N Willekeurige waarden normaal verdeeld. In dit geval de willekeurige vector X heeft N onafhankelijke componenten en daarom wordt gezegd dat X heeft n Graden van vrijheid.

Laten we de vector nu bouwen R van het afval

R = (x₁ - , X₂ - ,.. ., X_N - ))

Waar het het gemiddelde van het monster vertegenwoordigt, dat als volgt wordt berekend:

= (x₁ + X₂ +.. .+ X_N) / N

Dan de som

(X₁ - )+(x₂ - )+.. .+(X_N - ) = (x₁ + X₂ +.. .+ X_N) - n = 0

Het is een vergelijking die een beperking (of ligatie) in de vectorelementen vertegenwoordigt R van het afval, want als n-1 bekend zijn, vectorcomponenten R, De restrictie -vergelijking bepaalt de onbekende component.

Daarom de vector R van dimensie n met de beperking:

∑ (x_Je - ) = 0

Heeft (N - 1) vrijheidsgraden.

Nogmaals wordt toegepast dat de berekening van het aantal vrijheidsgraden is:

vrijheidsgraden: = n (dimensies) - 1 (beperkingen) = n -1

Voorbeelden

Variantie en vrijheidsgraden

De variantie s² Het wordt gedefinieerd als het gemiddelde van het kwadraat van de afwijkingen (of afval) van de gegevensmonster:

S² = (R•R) / (N-1)

waar R is de afvalvector R = (x1 -, x2 -, .. ., Xn -) en het dikke punt (•) is de scalaire productoperator. Als alternatief kan de variantieformule als volgt worden geschreven:

S² = ∑ (x_Je - ))² / (N-1)

In ieder geval moet worden opgemerkt dat bij het berekenen van het gemiddelde van het kwadraat van het afval, het wordt gedeeld door (n-1) en niet tussen n, zoals besproken in de vorige sectie, het aantal vrijheidsgraden van de vector R is (n-1).

Als voor de berekening van de variantie deze is verdeeld tussen N In plaats van (n-1) zou het resultaat een vooringenomenheid hebben die erg belangrijk is voor waarden van N Minder dan 50.

Het kan u van dienst zijn: analytische geometrie

In de literatuur verschijnt ook de formule van de variantie met de deler n in plaats van (n-1), als het gaat om de variantie van een populatie.

Maar de set van de willekeurige variabele van het afval, vertegenwoordigd door de vector R, Hoewel het dimensie N heeft, heeft het alleen (N-1) vrijheidsgraden. Als het gegevensnummer echter groot genoeg is (n> 500), komen beide formules samen naar hetzelfde resultaat.

De rekenmachines en spreadsheets bieden de twee versies van de variantie en de standaardafwijking (die de vierkantswortel van de variantie is).

Onze aanbeveling, gezien de hier gepresenteerde analyse, is om de versie altijd te kiezen met (n-1) elke keer dat het nodig is om de variantie of standaardafwijking te berekenen, om resultaten met bias te voorkomen.

In de chi -vierkante verdeling

Sommige waarschijnlijkheidsverdelingen in continue willekeurige variabele zijn afhankelijk van een parameter met de naam graad van vrijheid, Dit is het geval van de chi -vierkante verdeling (χ²)).

De naam van de genoemde parameter komt alleen uit de vrijheidsgraden van de willekeurige vector die ten grondslag ligt waarop deze verdeling wordt toegepast.

Neem aan dat er G -populaties zijn, waarvan N -maatmonsters worden genomen:

X₁ = (x1₁, X1₂,... x1_N))

X2 = (x2₁, X2₂,... x2_N))

.. .

X_J = (XJ₁, XJ₂,… XJ_N))

.. .

XG = (xg₁, XG₂,… Xg_N))

Een bevolking J dat heeft een gemiddelde en standaardafwijking SJ, Volg de normale verdeling n (, SJ )).

De getypeerde of genormaliseerde variabele ZJ_Je is gedefinieerd als:

Zj_Je = (XJ_Je - ) / SJ.

En de vector Zj Het is zo gedefinieerd:

Zj = (ZJ₁, Zj₂,…, ZJ_Je,…, ZJ_N) En volg de normale verdeling getypeerde n (0,1).

Dan de variabele:

Q = ((Z1₁ ^2 + Z2₁^2+… . + Zg₁^2),… ., (Z1_N^2 + Z2_N^2+… . + Zg_N^2))

Volg de verdeling χ²(g) de Chi -vierkante verdeling met de mate van vrijheid G.

In het hypothesecontrast (met een opgelost voorbeeld)

Wanneer u een hypothesecontrast wilt maken op basis van een bepaalde set willekeurige gegevens, is het noodzakelijk om de Aantal vrijheidsgraden G Om de Chi Square -test toe te passen.

Kan u van dienst zijn: continue uniforme verdeling: kenmerken, voorbeelden, toepassingen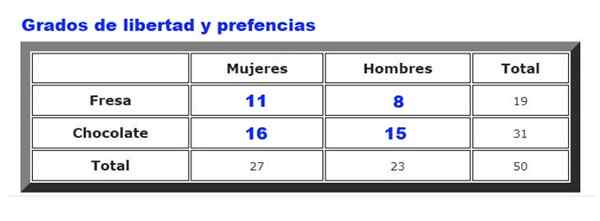 Figuur 2. Is er een relatie tussen ijsmaak en het geslacht van de klant? Bron: f. Zapata.

Als voorbeeld worden de gegevens die worden verzameld over chocolade- of aardbeienijsvoorkeuren tussen mannen en vrouwen in een ijswinkel geanalyseerd. De frequentie waarmee mannen en vrouwen aardbei of chocolade kiezen, is samengevat in figuur 2.

Eerst wordt de verwachte frequentietabel berekend, die wordt gemaakt door de Totale rijen voor hem Totale kolommen, gedeeld door Totale gegevens. Het resultaat wordt getoond in de volgende figuur:

figuur 3. Berekening van verwachte frequenties op basis van de waargenomen frequenties (blauwe waarden in figuur 2). Bron: f. Zapata.

Vervolgens gaan we verder met het berekenen van het chi -vierkant (uit de gegevens) door de volgende formule:

χ² = ∑ (f_of - F_En))² / F_En

Waar f_of zijn de waargenomen frequenties (figuur 2) en f_En zijn de verwachte frequenties (figuur 3). De som is over alle rangen en kolommen, die in ons voorbeeld vier termen geven.

Na het uitvoeren van de operaties krijgt u:

χ² = 0,2043.

Het is nu nodig om te vergelijken met het theoretische vierkant, dat afhangt van de Aantal vrijheidsgraden G.

In ons geval wordt dit aantal als volgt bepaald:

G = (#filas - 1) (#Columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Het blijkt dat het aantal vrijheidsgraden G van dit voorbeeld 1 is.

Als u de nulhypothese wilt verifiëren of afwijzen (H0: Er is geen correlatie tussen smaak en geslacht) met een significantieniveau van 1%, wordt het theoretische chi -vierkant berekend met de mate van vrijheid g = 1.

De waarde die de opgebouwde frequentie maakt, wordt gevraagd (1 - 0.01) = 0.99, dat is 99%. Deze waarde (die kan worden verkregen uit de tabellen) is 6.636.

Terwijl de theoretische chi de berekende overtreft, wordt de nulhypothese geverifieerd.

Dat wil zeggen, met de verzamelde gegevens, is er geen verband tussen de smaak van de variabelen en het geslacht.

Referenties

1. Minitab. Wat zijn de vrijheidsgraden? Opgehaald uit: ondersteuning.Minitab.com.
2. Moore, David. (2009) Basis -toegepaste statistieken. Antoni Bosch -redacteur.
3. Leigh, Jennifer. Hoe u vrijheidsgraden berekent in statistische modellen. Hersteld van: geniolandia.com
4. Wikipedia. Mate of Freedom (Statistics). Hersteld van: is.Wikipedia.com
5. Wikipedia. Mate van vrijheid (fysiek). Hersteld van: is.Wikipedia.com