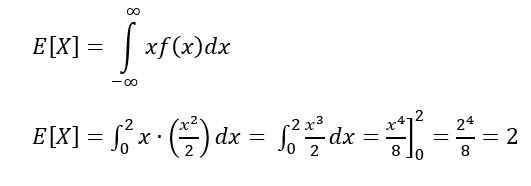Continue willekeurige variabele

We leggen uit wat een continue willekeurige variabele, de kenmerken, voorbeelden en een opgeloste oefening zijn

Wat is een continue willekeurige variabele?

A Continue willekeurige variabele Het is een willekeurig numerieke waarde verkregen, wat het gevolg is van het uitvoeren van een experiment en oneindige waarden kan nemen. Dit betekent dat, bekende twee opeenvolgende waarden van de variabele, het altijd mogelijk is om een ​​andere tussenliggende waarde ertussen te vinden.

Door een oneindige hoeveelheid waarden te hebben, is het verzamelen van continue variabele waarden niet boekhouding en behoort bijna altijd tot de reeks reële getallen.

Voorbeelden van dit type variabelen zijn de gestalte, het gewicht en de lichaamstemperatuur van een persoon, maar talloze ervan kunnen worden gedefinieerd, er zullen hieronder verschillende voorbeelden worden gevonden. In tegenstelling tot de continue willekeurige variabele, is er de discrete willekeurige variabele, die boekhouding is, zoals het aantal dochters in een gezin, of hoeveel auto's een bureau na een maand verkoopt.

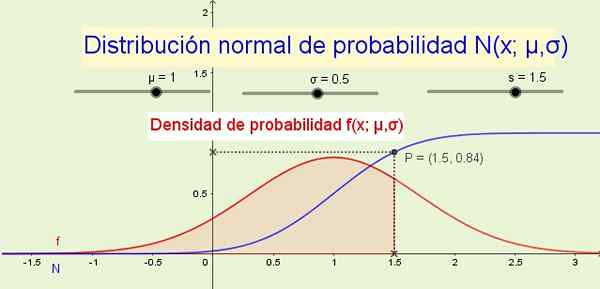
Discrete willekeurige variabelen volgen vaak de normale waarschijnlijkheidsverdeling. Bron: f. Zapata.

Een continue willekeurige variabele wordt aangegeven door middel van een kapitaalbrief zoals de X, en de oneindige waarden die de variabele neemt, zijn de mogelijke resultaten van het willekeurige experiment:

X = x₁, X₂, X₃,… ∞

Elke waarde heeft een zekere kans op voorkomen, en voor het model waarmee deze waarschijnlijkheid wordt berekend, wordt deze genoemd waarschijnlijkheidsverdeling.

Maar omdat X oneindige waarden neemt, kan de kans op specifieke waarden van de variabele niet worden berekend. Het is dus noodzakelijk om een ​​functie f (x) te definiëren, genoemd opgebouwde distributiefunctie, of eenvoudig distributiefunctie, volgens welke geaccumuleerde waarschijnlijkheid wordt berekend naar een bepaalde waarde of tussen twee waarden:

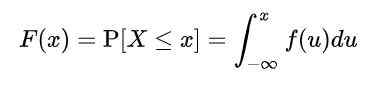
Waar f (u) Ontvang de naam van Dichtheidsfunctie. Op deze manier gedefinieerd, F (x) vertegenwoordigt de kans dat X is tussen -∞ en X.

Kenmerken van een continue willekeurige variabele

De continue willekeurige variabelen zijn voltooid F (x).

De dichtheidsfunctie F (x) Moet voldoen aan de volgende eigenschappen:

• De functie F (x) Het is positief: f (x)> = 0
• Het gebied onder de curve y = f (x) Het is altijd gelijk aan 1, dat wil zeggen dat de kans op het optreden van een of andere resultaat X In het interval (-∞, +∞) is 100%.
• De waarschijnlijkheid dat X in het interval is [a, b] wordt berekend door de volgende gedefinieerde integrale:

Kan u van dienst zijn: Curtosis: definitie, typen, formules, waarvoor bijvoorbeeld

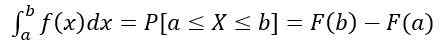
Die gelijkwaardig is aan het gebied onder de curve y = f (x), begrepen tussen naar En B. Daarnaast:

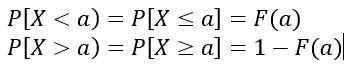
De waarden van F (x) Ze vertegenwoordigen geen kans, dus P [x = c] = 0. De relevante waarden zijn die welke overeenkomen met het gebied onder de curve y = f (x), die een waarschijnlijkheid vertegenwoordigen.

• Door de distributiefunctie af te leiden F (x) rekeninghoudend met X, is verkregen F (x).

De grafiek van F (x) Voor een continue willekeurige variabele is deze analoog aan de frequentie polygoon die is gebouwd voor een discrete statistische variabele, met het verschil dat, voor de willekeurige variabele, de breedte van het interval oneindig wordt.

Hoop

Hoop is een van de karakteristieke metingen van een continue variabele. De hoop of verwachte waarde van X Geeft de waarde aan die naar verwachting vaker zal optreden en wordt berekend door de volgende integraal:

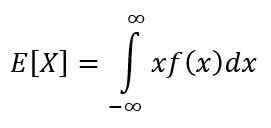
De eigenschappen zijn:

• E [a∙ x] = a∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+B∙ y] = a∙ e [x] + b∙ e [y]

Waar de bedragen naar En B Het zijn echte cijfers.

Voorbeelden

Zoals eerder aangegeven, zijn er veel situaties waarin een of meer continue willekeurige variabelen kunnen worden gedefinieerd. In wetenschap en andere gebieden zijn de meest voorkomende tijd, lengte, gewicht, volume en temperatuur:

Tijd

Om processen en diensten te optimaliseren, zijn experimenten ontworpen die de tijd die ze nemen om te worden uitgevoerd, bestuderen:

X = tijd die een klant naar het bankvenster brengt.

Y = wat een fastfood -plek inneemt bij het serveren van een bestelling.

Z = tijd waarin een bepaalde chemische reactie optreedt.

Structuren en gewichten

In veel studies over mensen en dieren zijn beelden en gewichten relevant:

X = meisjeshoogte in een 6e cursus. Graad in elke school in een stad.

Kan u van dienst zijn: congruentie: congruente cijfers, criteria, voorbeelden, oefeningen

Y = gewicht van baby's bij de geboorte in een openbaar ziekenhuis.

Z = het gewicht van de koeien op een boerderij.

Temperaturen

De temperatuur is een relevante parameter in tal van chemische processen, die meestal oneindige waarden in een bepaald bereik nodig hebben:

X = temperatuur waarbij een bepaalde chemische reactie optreedt, wetende dat dit optreedt tussen 80 ºC en 120 ºC.

Opgeloste oefeningen

Oefening 1

Bepaal wat de continue willekeurige variabelen zijn:

1. Het aantal studenten dat de koffie van de universiteit naar dag gaat naar de dag.
2. Bloeddruk van patiënten die naar een eerste hulp komen.
3. Lengte van vogelvleugels, van een bedreigde diersoort, die een reserve bewonen.
4. Tijd tussen de ene persoon en de andere wordt in een bank behandeld.
5. Hoeveelheid defecte producten per maand in een fabriek.
6. Cholesterolgehalte in de kippen van een boerderij.
7. Hoeveelheid straatlantaarns in een straat, van een totaal van 12.

Oplossing

1.- Het aantal studenten dat op de dag wordt gewerkt, is gevoelloos, daarom is deze variabele niet continu, maar discreet.

2.- Het is continu. De bloeddruk van patiënten kan elke waarde in een bepaald bereik nemen.

3.- Continue variabele, omdat de lengte van de vleugel van een vogel elke waarde tussen een minimum en een maximum neemt, afhankelijk van de soort.

4.- De tijd tussen de klantenservice is variabel en kan elke waarde in een bepaald bereik nemen, bijvoorbeeld tussen 1 en 5 minuten.

5.- Aangezien het aantal defecte producten boekhouding is, is het een discrete willekeurige variabele.

6.- Deze variabele is continu, omdat het niveau van cholesterol in de kippen elke waarde in een eerder bepaald bereik neemt.

Kan u van dienst zijn: complementaire hoeken: welke en hoe ze worden berekend, voorbeelden, oefeningen

7.- Discreet. Het aantal verlichtingslichten dat werkt, is een boekhoudhoeveelheid.

Oefening 2

Continue willekeurige variabele is gedefinieerd X = "cholesterolniveau " In een bepaalde verscheidenheid aan kippen van een boerderij, die de volgende dichtheidsfunctie heeft F (x):

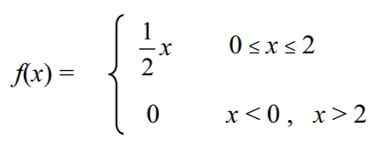
Bereken het volgende:

1. F (x)
2. P [x ≤2]
3. De hoop EX]

Oplossing voor

Volgens de definitie die in het begin wordt gegeven:

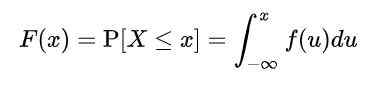
Daarom, F (x) Het is een functie in delen. Voor het interval X<0, F (x) Het is gelijk aan 0, voor de in het begin vermeld eigenschappen.

In de interval 0≤X≤2, Onbepaalde integrale is opgelost:

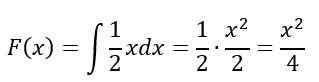
Ten slotte voor het interval X> 2, F (x) = 1, Volgens eigenschappen daarom, F (x) Het blijft zo:

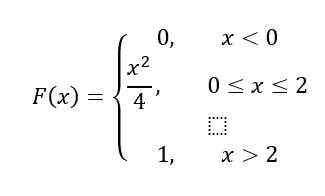
Oplossing B

De gewilde kans is F (1.2) en como x = 1.2 Het is gevonden tussen 0≤X≤2, dat deel van F (x) Evalueren:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Oplossing C

Om de hoop of verwachte waarde te berekenen, wordt deze gebruikt: