Hypothesetesten

Wat is hypothesetest?

De Hypothesetesten, In statistieken is het een procedure die wordt gebruikt om te controleren hoe succesvol een vermoeden is over een bevolking. Deze vermoedens worden genoemd hypothese, dat ze in principe als waar worden beschouwd, totdat enig bewijs het bevestigt of ontkent.

Dit bewijs wordt geleverd door steekproefgegevens, die uit een aanzienlijk deel van de bevolking komen, genaamd steekproef. De waarschijnlijkheidstheorie biedt de nodige technieken om de waarheidsgetrouwheid van de hypothesen te contrasteren.

Voorbeelden van hypothesen zijn:

-De gemiddelde temperatuur van het menselijk lichaam is 36.1 ºC.

-Gemiddeld weegt een zoute pindasas geproduceerd in een snacks -fabriek 50 g.

-80% van de inwoners van een stad, heeft de afgelopen 6 maanden online aankopen gedaan.

-IQ -testscores voor universitaire studenten van een goed bekende instelling, heeft een standaardafwijking van 15.

-Een bepaalde willekeurige variabele X volgt een Poisson -verdeling.

De eerste vier zijn van het type hypothese parametrisch, Omdat dit verklaringen zijn over een populatieparameter, zoals gemiddelde, standaardafwijking of een deel.

Aan de andere kant stelt de laatste hypothese de verdeling van een willekeurige variabele vast, en omdat deze niet verwijst naar een parameter of eigenschap van de populatie, wordt gezegd dat het een hypothese is niet parametrisch.

Null -hypothese en alternatieve hypothese

Er zijn twee soorten hypothese om een ​​test uit te voeren, die zal dienen om ze te contrasteren:

-Nulhypothese, aangeduid als h₀, stelt dat de onderzochte parameter een vastgestelde waarde heeft, of dat de willekeurige variabele een bepaalde verdeling volgt. Daarom, door symbolisch de nulhypothese uit te drukken, wordt het symbool van gelijkheid altijd gebruikt.

-Alternatieve hypothese: Geroepen h₁, Hij bevestigt dat de parameter of verdeling verschilt van wat de nulhypothese ervoor zorgt, dus, om symbolisch de alternatieve hypothese uit te drukken, worden de symbolen gebruikt: of ≠, maar nooit gelijkheid.

Het kan u van dienst zijn: Eigendom van Algebra Lock: Demonstration, Voorbeelden

Wanneer de nulhypothese wordt geaccepteerd, wordt de alternatieve hypothese afgewezen, zodat beide elkaar uitsluiten.

Mate van belang

Het is een maat voor de fout die kan worden gemaakt bij het uitvoeren van een hypothesetest. Het wordt gedefinieerd als de kans om de nulhypothese te verwerpen, omdat het waar is. Het wordt meestal aangeduid met de Griekse letter α:

α = P (verwerpen h₀ Als het waar is)

De waarden die vaak worden gebruikt voor α zijn 0.01, 0.05 en 0.10; De tweede zijn van het meest voorkomende gebruik. Gelijkwaardig tot respectievelijk 1%, 5% en 10% kans om fouten te maken bij het afwijzen H₀, Maar in elk geval, hoe lager het significantieniveau, hoe betrouwbaarder het testresultaat.

De alfa -waarde (α) kan worden opgevat als de procentuele fractie van het rechterstaart (of links) gebied, in een normale verdeling getypeerd (μ = 0 en σ = 1) en deze waarden komen altijd voor bij z = 2,33 voor α voor α = 0.01; bij z = 1,65 voor α = 1,65 en bij z = 1,29 voor α = 0,1.

Stappen om een ​​hypothesetest uit te voeren

Stap 1

Definieer respectievelijk de nul- en alternatieve hypothesen. De nulhypothese stelt vast dat de onderzochte parameter, θ genaamd, gelijk is aan een referentiewaarde, aangeduid als θ₀:

H₀: θ = θ₀

Als de effecten van een medicijn bijvoorbeeld worden onderzocht op een bepaald kenmerk van een populatie laboratoriummuizen, beschouwt de nulhypothese dat dit medicijn geen verschil maakt in een dergelijk kenmerk en dat dit een constante waarde heeft θ₀.

Om de nulhypothese te symboliseren, wordt het teken van gelijkheid altijd gebruikt, aan de andere kant, de alternatieve hypothese maakt gebruik van een van de symbolen of ≠.

In het voorbeeld van het medicijn stelt de alternatieve hypothese vast dat de verbinding enig effect heeft op het kenmerk in kwestie. Daarom is dit groter, lager of gewoon anders dan de referentiewaarde θ₀.

Kan u van dienst zijn: Factoriële notatie: concept, voorbeelden en oefeningen

Stap 2

Kies het juiste significantieniveau, dat meestal wordt vastgesteld op 5 %, zoals eerder aangegeven.

Stap 3

Bepaal de populatie en extract daaruit de steekproef, of monsters, waarvan de analyse zal dienen om de hypothesen te contrasteren en de acceptatie of afwijzing van de nulhypothese te bepalen.

Stap 4

Kies en bereken de waarde van de proefstatistiek voor de verzamelde gegevens, waaruit het benodigde bewijs wordt verkregen om de beslissing te nemen om de nulhypothese te accepteren of te verwerpen. De keuze van de proefstatistiek hangt af van de geselecteerde parameter: gemiddelde, afwijking, verhouding of andere.

De proefstatistiek wordt verkregen door een monsterparameter om te zetten in een Z -score, een student, R Pearson of Chi Square -statistiek, volgens het geselecteerde experimentele ontwerp. Hier zijn formules voor.

Meestal, als de populatieparameter de gemiddelde μ is, is "x balk" het monstergemiddelde, de standaardafwijking σ is bekend en is de steekproefgrootte n> 30, de teststatistiek z_C Het wordt berekend met de Z -score:

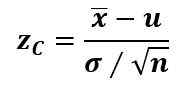
En wanneer n < 30, pero σ es desconocida, se usa la t de Student.

Stap 5

Stel criteria vast voor acceptatie of afwijzing van de nulhypothese, die kan worden gedaan via twee procedures:

• Via P -waarden.
• Door vergelijking met kritieke waarden.

P -waarden zijn gelijk aan de kans om de gevonden resultaten te verkrijgen, omdat de nulhypothese waar is. Als deze waarden klein zijn, wordt de nulhypothese afgewezen, als ze dat niet zijn, wordt deze geaccepteerd. In elk geval vormen P -waarden niet het bewijs dat de alternatieve hypothese waar is.

Er moet rekening mee worden gehouden dat het in een hypothese -test mogelijk is om twee soorten fouten te maken:

• Type I -fout: Verwerpen h₀ Als het waar is. De waarschijnlijkheid ervan is α en is equivalent aan het niveau van de bewijssignificantie.
• Type II -fout: Accepteer h₀ Als het eigenlijk onjuist is. De kans ervan wordt aangeduid als β.

Het kan u van dienst zijn: wat is de relatie tussen het rhombusgebied en de rechthoek?

Stap 6

De beslissing nemen om de nulhypothese te accepteren of af te wijzen. Als de waarden van P worden gebruikt, wanneer P < α, se rechaza H₀ En H wordt geaccepteerd₁, En anders wordt h geaccepteerd₀. De set van P -waarden < α se conoce como Kritische regio. Als de statistiek in dit interval is, wordt h afgewezen₀.

Evenzo wordt een kritieke waarde geselecteerd, volgens de gekozen populatieparameter. Als dit het gemiddelde is, ga dan als volgt verder:

• Test van een staart: θ < θ₀ of θ> θ₀
• Twee staarten test: | θ | < θ₀

Opgelost voorbeeld

Een machine produceert schroeven waarvan de nominale waarde 800 millimeter lang moet zijn, met een standaardafwijking van 5%.

Er wordt een willekeurig monster genomen, dat wil zeggen op verschillende dagen van de productieweek, die ongeveer 40 schroeven telt. Wanneer de gemiddelde lengte van het monster wordt berekend, wordt de waarde van 790 millimeter verkregen.

Bepaal of de gemiddelde lengte in tolerantie is met respectievelijk significantieniveaus van respectievelijk 1%, 5% en 10%.

Oplossing

De eerste is om de gemiddelde teststatistiek te berekenen, die in dit geval de afwijking is van het verdeelde gemiddelde tussen de standaard populatiefout:

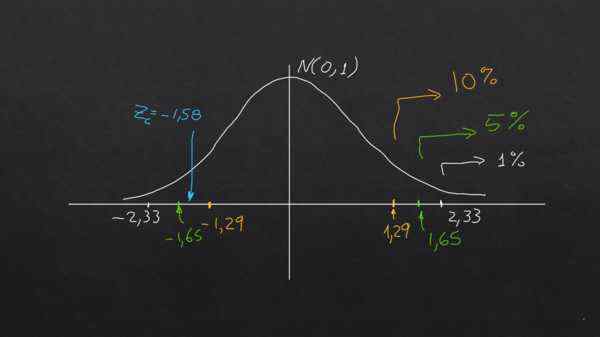
Zc = (790 - 800) / (40 / √40) = -1,58

Waar rekening is gehouden dat 5% standaardafwijking overeenkomt met 40 van 800.

De nulhypothese is dat het gemiddelde monster binnen de toegestane tolerantie valt tot het vereiste niveau van significantie, op voorwaarde dat | zc | is minder dan de getypeerde waarde | ZT |, anders wordt de nulhypothese afgewezen.

Voor betekenis van 1% en 5% wordt aan de nulhypothese voldaan, aangezien | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

Voor 10% betekenis gebeurt het echter dat | zc | > 1.29. Dat wil zeggen, op dit niveau van significantie wordt de nulhypothese niet gehaald.

De volgende grafiek verduidelijkt de conclusie:

De grafiek laat zien dat afhankelijk van het significantieniveau dezelfde hypothese vereist kan worden geaccepteerd of afgewezen met dezelfde gegevens. Bron: f. Zapata.