We leggen uit wat en wat de dispersiemaatregelen zijn, en we geven verschillende voorbeelden

Wat zijn dispersiemaatregelen?

De dispersiemaatregelen of van variatie, in statistieken, meet in hoeveel een verdeling van gegevens uit de waarde van een centrale maatregelbewegingen, zoals het gemiddelde of rekenkundig gemiddelde. De waarde ervan is altijd positief en normaal verschillend van 0, behalve in het geval van identieke gegevens.

Als een dispersiemaatregel een kleine waarde oplevert, betekent dit dat de gegevens zich zeer dicht bij het gemiddelde bevinden, maar als deze groot is, betekent dit dat de gegevens daarom meer verspreid zijn, weg van het gemiddelde.

Dispersiemaatregelen zijn erg belangrijk vanuit statistisch oogpunt, niet alleen als rekenkundige indicatoren voor gegevensvariatie, maar als een onschatbare hulp wanneer u de kwaliteit wilt verbeteren, zowel bij de productie van producten als bij het aanbieden van diensten.

Voorbeeld hiervan zijn de gelederen van aandacht bij de banken. De gemiddelde tijd die klanten uitstelt wanneer ze een unieke rij maken en vervolgens worden gedistribueerd in de kassa, is hetzelfde alsof ze afzonderlijke lijnen voor elk maken.

De dispersie is echter lager in de enkele rij, wat betekent dat individuele aandachtstijd erg lijkt op elke klant. Klanten hebben verklaard dat ze zich op deze manier op hun gemak voelen, zelfs als de gemiddelde zorgtijd in beide modaliteiten hetzelfde is.

Belangrijkste dispersiemaatregelen

De belangrijkste zijn: rang, variantie, standaardafwijking en variatiecoëfficiënt.

Bereik

De rang R van een gegevensset wordt gedefinieerd in het verschil tussen de maximale waarde x_Maximaal en de minimale waarde x_min Van het geheel:

Rang = r = maximale waarde - minimale waarde = x_Maximaal - X_min

Kan u van dienst zijn: waar zijn de cijfers voor? Het 8 belangrijkste gebruik

Het bereik is snel te berekenen, maar het is zeer gevoelig voor extreme waarden en heeft het nadeel dat het geen rekening houdt met tussenliggende waarden. Daarom wordt het alleen gebruikt om een ​​eerste, vrij geschat idee te hebben van de gegevensverspreiding.

Voorbeeld van rang

Dit is een lijst van het aantal orkanen in de Atlantische Oceaan in de afgelopen 14 jaar:

8; 9; 7; 8; vijftien; 9; 6; 5; 8; 4; 12; 7; 8; 2

De maximale waardegegevens zijn 15 en de minimumwaarde is daarom 2:

R = maximale waarde - minimale waarde = x_Maximaal - X_min = 15 - 2 = 13 orkanen

Variantie

Deze maatregel wordt gebruikt om elk van de gegevens te vergelijken met het gemiddelde van de set, en deze wordt berekend door de verschillen toe te voegen, vierkant hoog, tussen elke waarde met het gemiddelde en delen door het totale aantal waarden.

Zijn:

-Het gemiddelde: μ

-Elke waarde, behorend tot de gegevensset: x_Je

-Het totale aantal waarnemingen: n

Duiden op de variantie van een populatie als σ², De uitdrukking om te berekenen is:

En wanneer een steekproef van een populatie wordt genomen, heeft deze de voorkeur om de variantie op deze manier te berekenen:

Waarbij de steekproefvariantie is aangegeven met S en het gemiddelde als X met bar, om het gebruik van Griekse letters aan de bevolking over te laten. De reden om te delen tussen N-1, in plaats van N, is dat de steekproefvariantie de populatie niet onderschat, wat er altijd gebeurt wanneer deze zich verdeelt tussen n.

Aan de andere kant is het idee om elk verschil tussen gegevens en gemiddelde te kwets. In plaats daarvan zijn vierkanten altijd positief.

Het kan u van dienst zijn: frequentiekans: concept, hoe het wordt berekend en voorbeelden

Daarom is variantie altijd positief, zelfs als het verschil tussen x_Je En het gemiddelde is negatief, en het belangrijkste voordeel van de variantie is dat het rekening houdt met elke gegevens van de set.

Maar het heeft het ongemak dat zijn eenheden niet hetzelfde zijn als die van de gegevens, bijvoorbeeld, als deze in tijden bestaan, gemeten in minuten, wordt de variantie van de set in minuten aan het vierkant gegeven.

Voorbeeld van variantie

De berekening van de variantie vereist het vinden van het gemiddelde. Als u de gegevens van de orkaannummer gebruikt, wordt het gemiddelde berekend door:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 orkanen.Daarom is de variantie:

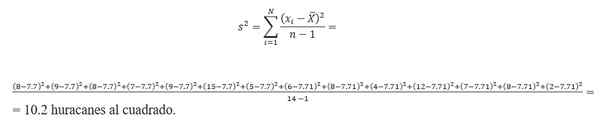
Standaardafwijking

Om het probleem van gebrek aan overeenstemming tussen de eenheden te verhelpen, is de standaardafwijking gedefinieerd σ, Zoals de vierkantswortel van de variantie:

En analoog, in het geval van een monster:

Er is een empirische regel om de waarde van de standaardafwijking van een steekproefgegevensset te schatten, gebaseerd op het bereik. Volgens deze regel is de standaardafwijking ongeveer een kwart van R:

S ≈ R/4

Het heeft het voordeel dat het een snelle schatting van de standaardafwijking toestaat, omdat de activiteiten veel eenvoudiger zijn.

De standaardafwijking is, met veel, de meest gebruikte dispersiemaatregel, dus het is de moeite waard om de belangrijkste kenmerken te benadrukken:

• De standaardafwijking geeft aan hoeveel de mediagegevens weggaan
• Het is altijd positief, maar het kan 0 zijn als alle gegevens identiek zijn
• Hoe groter de waarde van de standaardafwijking, hoe meer verspreid de gegevens zijn
• De standaardafwijkingseenheden zijn dezelfde als die van de variabele die wordt bestudeerd
• De waarde ervan verandert snel wanneer een van de gegevens (of meer) een zeer andere waarde heeft dan de rest
• De standaardafwijkingswaarden zijn bevooroordeeld, dat wil zeggen dat de gemiddelden van de standaardafwijking niet worden verdeeld over het gemiddelde, in tegenstelling tot de variantie, die niet -gebiaged is.

Kan u van dienst zijn: Acutangle Triangle

Voorbeeld van standaardafwijking

Doorgaan met het voorbeeld van orkanen, is de standaardafwijking:

Of, als het de voorkeur heeft om de benadering van de standaardafwijking door het bereik te gebruiken, wordt een vrij nauwe waarde verkregen:

S = 13/4 = 3.25

Variatiecoëfficiënt

De variatiecoëfficiënt wordt aangegeven door de initialen CV of R, in sommige teksten, en zowel voor een populatie als voor een steekproef, relateert de standaard en gemiddelde afwijking, als een percentage:

O goed:

De vergelijkingen zijn geldig zolang het gemiddelde verschilt van 0.

In de regel wordt de variatiecoëfficiënt afgerond op een enkel decimaal en wordt gebruikt om gegevens van twee verschillende populaties te vergelijken.

Voorbeeld van variatiecoëfficiënt

Wachttijden in seconden, voor de klanten van een bank, worden in twee situaties opgenomen: wanneer ze een unieke rij maken en wanneer ze individuele rangen maken voor het aandachtskantoor. De resultaten zijn de volgende:

Beide gegevenssets kunnen worden vergeleken door hun respectieve variatiecoëfficiënt:

Enkele rij

• Gemiddeld = 429 seconden
• Afwijking = 28.6 seconden
• CV = (28.6/429) x 100 = 6.7 %

Individuele rangen

• Gemiddeld = 429 seconden
• Afwijking = 109.3 seconden
• CV = (109.3/429) x 100 = 25.5 %

Omdat deze laatste waarde groter is, geeft dit aan dat er meer variabiliteit is in klantenservicetijden wanneer ze individuele rangen maken dan wanneer ze een unieke rij maken, hoewel de gemiddelde tijd in elk geval hetzelfde is.