Fourier discrete getransformeerde eigenschappen, toepassingen, voorbeelden

De Fourier discreet getransformeerd Het is een numerieke methode die wordt gebruikt om monsters te definiëren die verband houden met de spectrale frequenties die een signaal vormen. Studies periodieke functies in gesloten parameters, die daardoor een ander discreet signaal gooien.

Om de discrete transformatie van furier van n punten te verkrijgen, moeten op een discreet signaal aan de volgende 2 voorwaarden op een reeks worden voldaan X [n]

 x [n] = 0   N n - 1

Het vervullen van deze voorwaarden kan de discrete transformatie van Fourier worden gedefinieerd als

TDF

De discrete transformatie van Fourier kan worden gedefinieerd als een bemonstering op N -punten van de Fourier -transformatie.

[TOC]

Interpretatie van Fourier's discrete transformatie

Bron: Pexels

Er zijn 2 gezichtspunten waaruit de resultaten op een reeks X kunnen worden geïnterpreteerd_S[n] door de discrete transformatie van Fourier.

-De eerste komt overeen met de spectrale coëfficiënten, al bekend bij de Fourier -serie. Het wordt waargenomen in discrete periodieke signalen, waarbij monsters samenvallen met sequentie X_S[N].

-De tweede gaat over het spectrum van een discrete aperiadisch signaal, met monsters die overeenkomen met sequentie X_S[N].

De discrete transformatie is een benadering van het spectrum van het oorspronkelijke analoge signaal. De fase hangt af van bemonsteringsmomenten, terwijl de omvang ervan afhangt van het bemonsteringsinterval.

Eigenschappen

De algebraïsche structuur vormen de logische basis van de volgende secties.

Lineariteit

C . S_N → c . F[S_k]; Als een reeks wordt vermenigvuldigd met een scalaire, zal de transformatie ook zijn.

T_N + V_N = F [T_k]+F [V_k]; De transformatie van een som is gelijk aan de som van de getransformeerde.

Dualiteit

F [s_N] → (1/n) s_-K; Als de discrete transformatie van Fourier wordt teruggeroepen naar een reeds getransformeerde uitdrukking, wordt dezelfde uitdrukking verkregen, klimmen in N omgekeerd ten opzichte van de verticale as.

Convolutie

De convolutie van functies achtervolgt soortgelijke doelstellingen die in de Laplace -transformatie verwijst naar het product onder zijn Fourier -transformaties. De convolutie is ook van toepassing op discrete tijden en is verantwoordelijk voor veel moderne procedures.

X_N * R_N → f [x_N] .F [r_N]; De transformatie van een convolutie is gelijk aan het product van die getransformeerd.

X_N . R_N→ f [x_N] * F [r_N]; De transformatie van een product is gelijk aan de convolutie van de getransformeerde.

Verplaatsing

X_N-M → f [x_k] e ^{-I (2π/n) km} ; Als een opvolging wordt vertraagd in M ​​-monsters, is het effect op de discrete transformatie een wijziging van de hoek die wordt gedefinieerd door (2π/n) km.

Kan u van dienst zijn: waarom is algebra belangrijk in bepaalde situaties in het dagelijkse leven?

Symmetrie geconjugeerd

X_T [-K] = x*_T[k] = x_T [N - K]

Modulatie

W^-nm_N . x [n] ↔ x_T[K - M]

Product

x [n] y [n] ↔ (1/n) x_T[k]*en_T[K]

Symmetrie

X [-n] ↔ x_T[-K] = x*_T[K]

Conjugeren

x*[n] ↔ x*_T[-K]

Parseval -vergelijking 

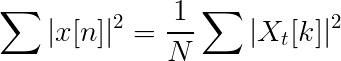
Overeenkomsten en verschillen met de Fourier -transformatie

Met betrekking tot de conventionele transformale van Fourier heeft het verschillende overeenkomsten en verschillen. Fourier's transformatie zet een reeks om in een continue lijn. Op deze manier wordt gezegd dat het resultaat van de Fourier -variabele een complexe reële variabele functie is.

De discrete transformatie van Fourier ontvangt, in tegenstelling tot een discreet signaal en transformeert het in een ander discreet teken, dat wil zeggen een reeks.

Wat is het nut van Fourier's discrete transformatie?

Ze dienen voornamelijk tot belangrijke vergelijkingen, terwijl ze uitdrukkingen transformeren die zijn afgeleid in machtselementen. Differentiële uitdrukkingen aangeven in vormen van integreerbare polynomen.

In de optimalisatie, modulatie en modellering van resultaten werkt het als een gestandaardiseerde expressie, een frequente bron voor engineering na verschillende generaties.

Bron: Pixabay

Geschiedenis

Dit wiskundige concept werd gepresenteerd door Joseph B. Fourier in 1811, tijdens het ontwikkelen van een verdrag over de Warmte verspreid. Het werd snel overgenomen door verschillende takken van wetenschap en engineering.

Het werd vastgesteld als het belangrijkste werkinstrument in de studie van vergelijkingen met gedeeltelijke derivaten, zelfs met de werkrelatie tussen de Laplace getransformeerde en gewone differentiaalvergelijkingen.

Elke functie die met Fourier -transformatie kan worden bewerkt, moet nietigheid buiten een gedefinieerde parameter presenteren.

Fourier discreet getransformeerd en zijn omgekeerde

De discrete transformatie wordt verkregen door de uitdrukking:

Na een discrete volgorde x [n]

De inverse van Fourier's discrete transformatie wordt gedefinieerd door de uitdrukking:

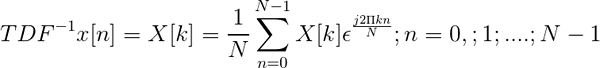Inverse TDF

Het staat toe dat zodra het discrete is getransformeerd, de volgorde in het tijddomein x [n] definieert, definieert.

Opschik

Het parameterisatieproces dat overeenkomt met de discrete transformatie van Fourier ligt in de welp. Om de transformatie te werken, moeten we de reeks in de tijd beperken. In veel gevallen hebben de signalen in kwestie deze beperkingen niet.

Een opvolging die niet voldoet aan de groottecriteria om toe te passen op de discrete transformatie, kan worden vermenigvuldigd met een "venster" V [n] -functie, waardoor het gedrag van de opvolging in een gecontroleerde parameter wordt gedefinieerd.

Kan u van dienst zijn: cirkelvormige permutaties: demonstratie, voorbeelden, opgeloste oefeningen

X [n] . V [n]

De spectrumbreedte is afhankelijk van de vensterbreedte. Naarmate de vensterbreedte toeneemt, zal de berekende getransformeerde smaller zijn.

Toepassingen

Berekening van de fundamentele oplossing

Fourier's discrete transformatie is een krachtig hulpmiddel in de studie van discrete opvolgingen.

Fourier's discrete transformatie transformeert een continue variabele functie, in een discrete variabele transformatie.

Cauchy's probleem voor warmtevergelijking biedt een frequent toepassingsveld van Fourier's discrete transformatie. Waar de functie wordt gegenereerd Dirichlet warmte of kernkern, die van toepassing is op waardenbemonstering in een gedefinieerde parameter.

Signaaltheorie

De algemene reden voor de toepassing van Fourier's discrete transformatie in deze tak is vooral te wijten aan de karakteristieke ontleding van een signaal als een oneindige overlapping van gemakkelijker behandelbare signalen.

Het kan een geluidsgolf of een elektromagnetische golf zijn, de discrete transformatie van Fourier drukt het uit in een eenvoudige golfoverlap. Deze weergave komt vrij vaak voor in elektrotechniek.

Fourier's serie

Ze zijn gedefinieerde series in termen van cosenos en borsten. Ze dienen om het werk te vergemakkelijken met algemene periodieke functies. Wanneer ze worden toegepast, maken ze deel uit van de resolutietechnieken van gedeeltelijke en gewone differentiaalvergelijkingen.

Fourier -series zijn nog algemener dan de serie van Taylor, omdat ze periodieke discontinua -functies ontwikkelen die geen weergave hebben in Taylor -serie.

Andere vormen van de Fourier -serie

Om de transformatie van Fourier analytisch te analyseren, is het belangrijk.

-Fourier -serie over een functie van 2l periode:

Vaak is het noodzakelijk om de structuur van een Fourier-serie aan te passen aan periodieke functies waarvan de periode P = 2L> 0 is in het interval [-l, l].

-Fourier -serie in even en oneven functies

Het interval [-π, π] wordt overwogen die voordelen biedt bij het profiteren van de symmetrische kenmerken van de functies.

Kan u van dienst zijn: eindige set: eigenschappen, voorbeelden, opgeloste oefeningen

Als f koppel is, wordt de Fourier -serie vastgesteld als een reeks cosenos.

Als f vreemd is, is de Fourier -serie opgericht als een reeks borsten.

-Complexe notatie van de Fourier -serie

Als u een F (t) -functie heeft, die voldoet aan alle vereisten van de Fourier-serie, is het mogelijk om deze in het interval aan te geven [-t, t] met behulp van de complexe notatie: 

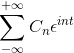
Voorbeelden

Wat betreft de berekening van de fundamentele oplossing, worden de volgende voorbeelden gepresenteerd:

Laplace -vergelijking

Warmtevergelijking

Schrödinger -vergelijking

Golfvergelijking

Aan de andere kant zijn er voorbeelden van toepassing van Fourier's discrete transformatie op het gebied van signaaltheorie:

-Systeemidentificatieproblemen. Gevestigd f en g

-Probleem met de consistentie van het uitgangssignaal

-Problemen met het signaalfiltering

Opdrachten

Oefening 1

Bereken de discrete transformatie van Fourier voor de volgende opvolging.

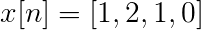
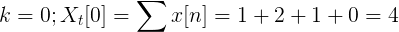
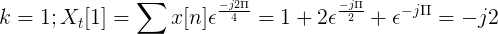
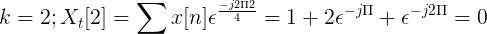
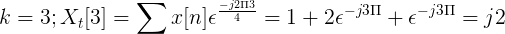
De X [N] TDF kan worden gedefinieerd als:

X_T[k] = 4, -j2, 0, j2 voor k = 0, 1, 2, 3

Oefening 2

Het is gewenst om door een digitaal algoritme het spectrale signaal te bepalen dat wordt gedefinieerd door de expressie x (t) = e^-T. Waarbij de maximale frequentieaanvraagcoëfficiënt f is_M= 1Hz. Een harmonische komt overeen met F = 0.3 Hz. De fout is beperkt tot minder dan 5%. Berekenen F_S , D en n.

Rekening houdend met de bemonsteringsstelling F_S = 2f_M = 2 Hz

Een frequentieresolutie van F₀ = 0.1 Hz, waarbij d = 1/0,1 = 10s worden verkregen

0.3 Hz is de frequentie die overeenkomt met index k = 3, waarbij n = 3 × 8 = 24 monsters. Aangeeft dat F_S = N/d = 24/10 = 2.4> 2

Omdat het doel is om de minst mogelijke waarde voor N te bereiken, kunnen de volgende waarden als een oplossing worden beschouwd:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33S

K = 1

N = 1 × 8 = 8

Referenties

1. De discrete Fourier -transformatie beheersen in één, twee of meerdere dimensies: valkuilen en artefacten. Isaac Amidor. Springer Science & Business Media, 19 juli. 2013
2. De DFT: een handleiding van een eigenaren voor de discrete Fourier -transformatie. William L. Briggs, van Emden Henson. Siam, 1 januari. negentienvijfennegentig
3. Digitale signaalverwerking: theorie en praktijk. D. Sundararajan. World Scientific, 2003
4. Transformeert en snelle algoritmen voor signaalanalyse en representaties. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6 december. 2012
5. Discrete en continue Fourier -transformaties: analyse, toepassingen en snelle algoritmen. Eleanor Chu. CRC Press, 19. 2008