Fundamentele stelling van rekenkundige demonstratie, toepassingen, oefeningen

Hij De fundamentele stelling van rekenkunde Hij stelt dat elk natuurlijk getal groter dan 1 kan worden opgesplitst als een product van priemgetallen - en wat vasthouden - en deze vorm is uniek voor dat aantal, hoewel de volgorde van de factoren anders kan zijn.

Onthoud dat een priemgetal P Het is degene die alleen als positieve divisors zelf en 1 toegeeft. De volgende nummers zijn neven: 2, 3, 5, 7, 11, 13 enzovoort, omdat er oneindig is. Nummer 1 wordt niet beschouwd als neef, voor het hebben van een enkele deler.

Figuur 1. Euclides (links) demonstreerde de fundamentele stelling van rekenkunde in zijn boekelementen (350 a.C.), En de eerste volledige demonstratie is te wijten aan Carl F. Gauss (1777-1855) (rechts). Bron: Wikimedia Commons.

Van hun kant worden getallen die niet aan het bovenstaande voldoen, aangeroepen Samengestelde nummers, As 4, 6, 8, 9, 10, 12, 14 ... Laten we bijvoorbeeld nummer 10 nemen en onmiddellijk zien we dat het kan worden afgebroken als een product van 2 en 5:

10 = 2 × 5

Zowel 2 als 5 zijn inderdaad priemgetallen. De stelling stelt dat dit mogelijk is voor elk getal n:

Waar P₁, P₂, P₃… P_R Het zijn priemgetallen en k₁, k₂, k₃,... K_R Het zijn natuurlijke cijfers. Zodat priemgetallen werken als bakstenen waaruit, met vermenigvuldiging, natuurlijke nummers zijn gebouwd.

[TOC]

Demonstratie van de fundamentele stelling van rekenkunde

Het begint aan te tonen dat elk getal in topfactoren kan ontleden. Wees een natuurlijk nummer n> 1, neef of compound.

Als bijvoorbeeld n = 2, kan dit worden uitgedrukt als: 2 = 1 × 2, wat neef is. Op dezelfde manier gaan we verder met de volgende nummers:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

We gaan zo door, waarbij we alle natuurlijke nummers ontbinden totdat we nummer n -1 bereiken. Laten we kijken of we het kunnen doen met het nummer dat volgt: n.

Als n neef is, kunnen we het ontbinden als n = 1 × n, maar veronderstellen dat n is samengesteld en een deler d heeft, logisch minder dan n:

Kan u van dienst zijn: beschrijvende statistieken: geschiedenis, kenmerken, voorbeelden, concepten

1< d < n.

Ja n/d = p₁, met P₁ Een priemgetal, dan is n geschreven als:

n = P₁.D

Als D neef is, is er niets meer te doen, maar als dit niet het geval is, is er een nummer n₂ dat is een deler van D en minder dan dit: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Voor een ander neefnummer P₂:

D = P₂ N₂

Dat door het vervangen van het oorspronkelijke nummer N zou geven:

n = P₁ .P₂ .N₂

Stel nu n₂ Het is ook niet een priemgetal en we schrijven het als het product van een priemgetal P₃, voor een deler van hem₃, zodanig dat n₃ < n₂ < n₁ < n:

N₂ = P₃.N₃ → n = p₁ P₂ P₃.N₃

 We herhalen deze procedure een eindig aantal keren totdat u krijgt:

n = P₁.P₂.P₃ … P_R

Dit betekent dat het mogelijk is om alle hele getallen van 2 tot nummer N te ontleden, als een product van priemgetallen.

Uniekheid van ontleding in topfactoren

Laten we nu verifiëren dat deze ontleding, behalve de volgorde van de factoren, uniek is. Stel dat u op twee manieren kunt schrijven:

n = P₁.P₂.P₃ … P_R = q_1.Q₂.Q₃… Q_S  (met r ≤ s)

Natuurlijk Q₁, Q₂, Q₃... het zijn ook priemgetallen. Als p₁ Verdeel naar (Q_1.Q₂.Q₃… Q_S) Dan p₁ Het is gelijk aan een van de "q", ongeacht Welke, dus we kunnen dat p zeggen₁ = q₁. We verdelen n tussen p₁ En we krijgen:

P₂.P₃ … P_R =_.Q₂.Q₃… Q_S

We herhalen de procedure om alles tussen p te verdelen_R, Dan krijgen we:

1 = Q_R+1… Q_S

Maar het is niet mogelijk om naar Q te komen_R+1… Q_S = 1 wanneer r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Toepassingen

Zoals we eerder hebben gezegd, vertegenwoordigen de priemgetallen als u wilt, de atomen van de cijfers, hun basiscomponenten. Dus de fundamentele stelling van rekenkunde heeft talloze toepassingen, het meest voor de hand liggende: we kunnen gemakkelijker werken met grote aantallen als we ze uitdrukken als het product van kleinere getallen.

Kan u van dienst zijn: hele nummers

Op dezelfde manier kunnen we het maximale gemeenschappelijke meervoud vinden (m.C.M.) en de maximale gemeenschappelijke deler (m.C.D.), Een procedure die ons helpt om sums van breuken gemakkelijker te maken, wortels van grote aantallen te vinden, of te werken met radicalen, rationaliseer en lost de problemen van de toepassing van zeer diverse aard op.

Bovendien zijn priemgetallen extreem raadselachtig. Een patroon wordt er nog niet in herkend en het is niet mogelijk om te weten wat het volgende zal zijn. De grootste tot de tijden werden gevonden door computers en heeft 24.862.048 cijfers, Hoewel de nieuwe priemgetallen elke keer minder vaak verschijnen.

Primo -getallen in de natuur

De cicaden, cycake of chicharras die in het noordoosten van de Verenigde Staten wonen, komen in 13 of 17 jaar cycli op. Beide zijn priemgetallen.

Op deze manier vermijdt Chicharras samenvallen met roofdieren of concurrenten met andere geboorteperioden, noch de verschillende Chicharra -variëteiten concurreren met elkaar, omdat ze niet samenvallen in hetzelfde jaar.

Figuur 2. De geageerde cicada del este van de Verenigde Staten komt elke 13 of 17 jaar naar voren. Bron: PxFuel.

Primo -nummers en online aankopen

Primo -nummers worden gebruikt in cryptografie om de details van creditcards bij te houden wanneer u online aankopen koopt. Op deze manier zijn de gegevens die de koper precies aan de winkel aankomt zonder te verdwalen of in gewetenloze mensen te vallen.

Als? Kaartgegevens worden gecodeerd in een getal n dat kan worden uitgedrukt als het product van priemgetallen. Deze priemgetallen zijn de sleutel die de gegevens onthullen, maar ze zijn onbekend bij het publiek, ze kunnen alleen worden gedecodeerd op het web waarnaar ze zijn gericht.

Het ontbinden van een getal in factoren is een gemakkelijke taak als de cijfers klein zijn (de oefeningen zien opgelost), maar in dit geval worden ze gebruikt als belangrijke priemgetallen van 100 cijfers, die door ze te vermenigvuldigen veel grotere aantallen, waarvan de gedetailleerde ontleding een Enorm werk.

Kan u van dienst zijn: punctuele schatting

Opgeloste oefeningen

- Oefening 1

Ontbind 1029 in topfactoren.

Oplossing

1029 is deelbaar door 3. Het is bekend omdat door het toevoegen van uw cijfers de som een ​​veelvoud is van 3: 1+0+2+9 = 12. Aangezien de volgorde van de factoren het product niet verandert, kunnen we daar beginnen:

1029 3

343

1029 = 3 × 343

Aan de andere kant 343 = 7³, Dus:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

En omdat beide 3 en 7 priemgetallen zijn, is dit de ontleding van 1029.

- Oefening 2

Factor Trinomial X² + 42x + 432.

Oplossing

De trinomiale wordt herschreven in de vorm (x+a). (x+b) en we moeten de waarden van a en b vinden, zodat:

A+B = 42; naar.B = 432

Het nummer 432 ontleedt in topfactoren en van daaruit wordt het door Tanteo de juiste combinatie gekozen voor de feiten die zijn toegevoegd aan 42.

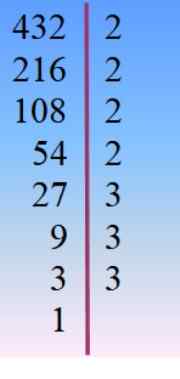
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

Vanaf hier zijn er verschillende mogelijkheden om 432 te schrijven:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

En alles kan worden gevonden door producten te combineren tussen prime -factoren, maar om de voorgestelde oefening op te lossen, is de enige adequate combinatie: 432 = 24 × 18 sinds 24 + 18 = 42, dan:

X² + 42x + 432 = (x + 24). (x +18)

Referenties

1. Baldor, een. 1986. Praktische theoretische rekenkunde. Editor Cultureel Company of American Texts S.NAAR.
2. BBC World. De verborgen natuurcode. Opgehaald uit: BBC.com.
3. Van Leon, Manuel.Primo -nummers: internet -bewakers. Hersteld van: blogs.20 minuten.is.
4. UNAM. Nummertheorie I: Fundamentele stelling van rekenkunde. Opgehaald uit: theoriadenumeros.Wikidot.com.
5. Wikipedia. De fundamentele stelling van rekenkunde. Hersteld van: is.Wikipedia.borg.