Hyperbolische paraboloïde definitie, eigenschappen en voorbeelden

A hyperbolisch paraboloïde Het is een oppervlak waarvan de algemene vergelijking in Cartesiaanse coördinaten (x, y, z) voldoet aan de volgende vergelijking:

(voor)² - (en B)² - Z = 0.

De "paraboloïde" denominatie komt van het feit dat variabele z afhankelijk is van de vierkanten van de X- en Y -variabelen. Terwijl het bijvoeglijk naamwoord "hyperbolisch" te wijten is aan het feit dat de vergelijking van een hyperbool een vaste waarden van z heeft. De vorm van dit oppervlak is vergelijkbaar met die van een paardrijstoel.

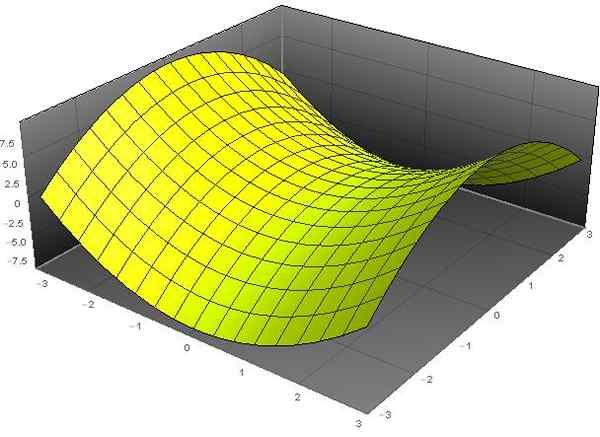
Figuur 1. Hyperbolische paraboloïde z = x² - En². Bron: f. Zapata via Wolfram Mathematica.

[TOC]

Beschrijving van de hyperbolische paraboloïde

Om de aard van de hyperbolische paraboloïde te begrijpen, zal de volgende analyse worden gemaakt:

1.- Het specifieke geval zal worden genomen a = 1, b = 1, dat wil zeggen dat de Cartesiaanse vergelijking van de paraboloïde blijft als z = x² - En².

2.- Ze worden beschouwd als parallelle vlakken voor het ZX -vlak, dat wil zeggen y = ctte.

3.- Met y = ctte is het z = x² - C, die gelijkenissen vertegenwoordigt met de takken omhoog en hoekpunt onder het xy -vlak.

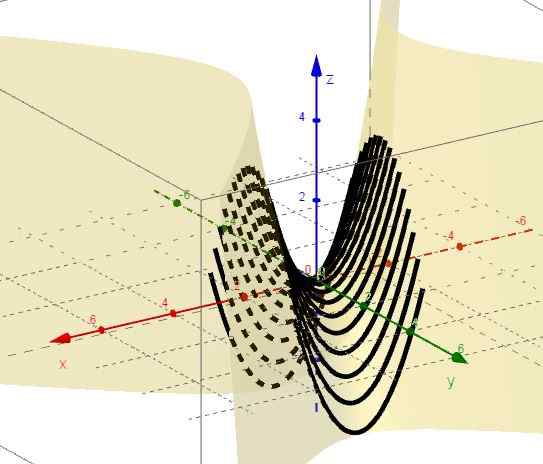Figuur 2. Familie van curven z = x² - C. Bron: f. Zapata door Geogebra.

4.- Met x = ctte is z = c - y², die gelijkenissen vertegenwoordigt met de takken naar beneden en hoekpunt boven het xy -vlak.

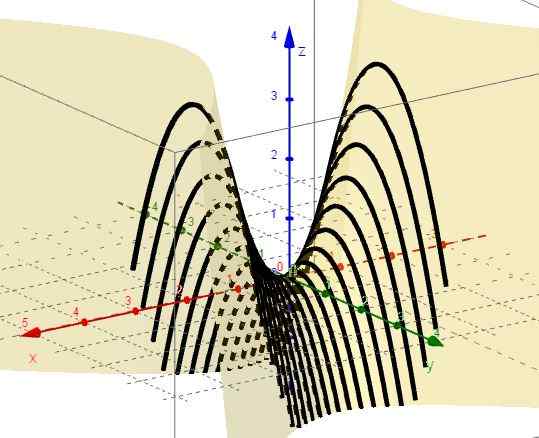figuur 3. Familie van curven Z = C - en². Bron: f. Zapata door Geogebra.

5.- Met z = ctte is c = x² - En², die hyperbolen vertegenwoordigen in vliegtuigen parallel aan het XY -vliegtuig. Wanneer C = 0 zijn er twee lijnen (A +45º en -45º ten opzichte van de X -as) die worden onderschept bij de oorsprong op het XY -vlak.

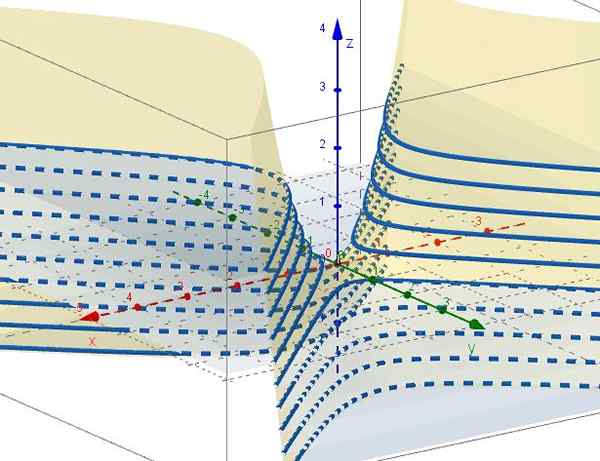Figuur 4. Familie van rondingen x² - En² = C. Bron: f. Zapata door Geogebra ..

Eigenschappen van hyperbolische paraboloïde

1.- Vier verschillende punten in de drie -dimensionale ruimte definiëren één en slechts een hyperbolische paraboloïde.

Het kan u van dienst zijn: Limiet Eigenschappen (met voorbeelden)

2.- Hyperbolische paraboloïde is een Douels gereguleerd oppervlak. Dit betekent dat, ondanks dat het een gebogen oppervlak is, voor elk punt van een hyperbolische paraboloïde twee verschillende lijnen volledig doorgaan naar de hyperbolische paraboloïde. Het andere oppervlak dat geen vlak is en dubbel is gereguleerd, is de Revolutie hyperboloid.

Het is precies de tweede eigenschap van de hyperbolische paraboloïde die er een breed gebruik van in architectuur toe heeft toegestaan, omdat het oppervlak kan worden gegenereerd uit balken of rechte strings.

De tweede eigenschap van de hyperbolische paraboloïde maakt een alternatieve definitie ervan mogelijk: Het is het oppervlak dat kan worden gegenereerd door een rechte mobiele lijn parallel aan een vast vlak en snijdt twee vaste lijnen die als gids dienen. De volgende figuur verduidelijkt deze alternatieve definitie van hyperbolische paraboloïde:

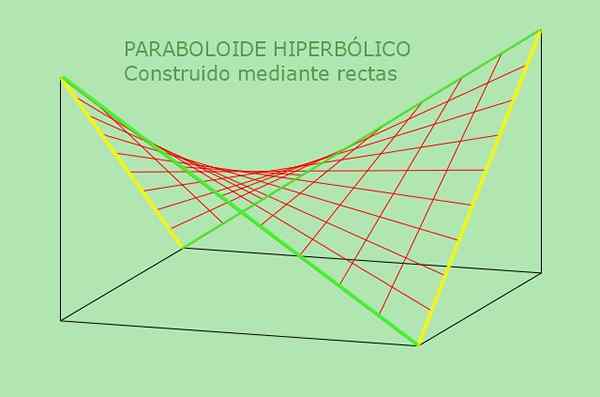Figuur 5. Hyperbolische paraboloïde is een dubbel gereguleerd oppervlak. Bron: f. Zapata.

Opgeloste voorbeelden

- voorbeeld 1

Toon aan dat de vergelijking: Z = xy, komt overeen met een hyperbolische paraboloïde.

Oplossing

Een transformatie zal worden toegepast in de x- en y -variabelen die overeenkomen met een rotatie van de Cartesiaanse assen ten opzichte van de z van +45 as. De oude X- en Y -coördinaten worden getransformeerd naar de nieuwe X 'E en' volgens de volgende relaties:

x = x ' - y'

y = x ' + en'

Hoewel de z -coördinaat hetzelfde blijft, is dat z = z '.

Door te vervangen in vergelijking Z = x en we hebben:

z '= (x' - y ') (x' + y ')

Bij het toepassen van het opmerkelijke product van het verschil door de som gelijk aan het verschil van vierkanten is het:

Z '= x'² - En'²

die duidelijk overeenkomt met de definitie die aanvankelijk wordt gegeven van hyperbolische paraboloïde.

De onderschepping van de vlakken parallel aan de XY -as met de hyperbolische paraboloïde z = x en bepalen gelijkzijdige hyperbolen die de vlakken hebben x = 0 e y = 0.

Kan u van dienst zijn: miletus Een dergelijke stelling

- Voorbeeld 2

Bepaal de parameters naar En B van de hyperbolische paraboloïde die door punten A gaat (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) en D (2, -1, 32/9).

Oplossing

Volgens zijn eigenschappen bepalen vier punten in de drie -dimensionale ruimte een enkele hyperbolische paraboloïde. De algemene vergelijking is:

Z = (x/a)² - (en B)²

We vervangen de gegeven waarden:

Voor punt a heb je 0 = (0/a)² - (0/B)², Vergelijking die voldoet aan de waarden van de parameters A en B.

Het vervangen van punt B wordt verkregen:

5/9 = 1/a² - 1 B²

Terwijl het voor punt C blijft:

32/9 = 4/A² - 1 B²

Ten slotte wordt het voor punt D verkregen:

32/9 = 4/A² - 1 B²

Die identiek is aan de vorige vergelijking. Kortom, het systeem van vergelijkingen moet worden opgelost:

5/9 = 1/a² - 1 B²

32/9 = 4/A² - 1 B²

Het aftrekken van de tweede vergelijking van de eerste wordt verkregen:

27/9 = 3/A² wat dat inhoudt² = 1.

Evenzo wordt de tweede vergelijking van de viervoud van de eerste afgetrokken, het verkrijgen:

(32-20)/9 = 4/A² - 4/A² -1 B² + 4/B²

Dat is vereenvoudigd als:

12/9 = 3/B² ⇒ B² = 9/4.

Kortom, de hyperbolische paraboloïde die door punten A, B, C en D wordt gegeven, heeft een Cartesiaanse vergelijking gegeven door:

Z = x² - (4/9) en²

- Voorbeeld 3

Volgens de eigenschappen van de hyperbolische paraboloïde passeren twee lijnen die er volledig in zijn opgenomen voor elk punt. Voor het geval z = x^2 - y^2 vind de vergelijking van de twee lijnen die door punt P (0, 1, -1) passeren die duidelijk tot de hyperbolische paraboloïde behoren, zodat alle punten van deze lijnen ook tot de dezelfde.

Oplossing

Met behulp van het opmerkelijke product van het verschil in vierkanten kan de vergelijking van de hyperbolische paraboloïde als volgt worden geschreven:

Kan u van dienst zijn: vierhoekig: elementen, eigenschappen, classificatie, voorbeelden

(x + y) (x - y) = c z (1/c)

Waar C een niet -nul constante is.

De vergelijking x + y = c z en vergelijking x - y = 1/c komen overeen met twee vlakken met normale vectoren N= Y M=. Het vectorproduct M x n = De richting van de lijntrok van de twee vliegtuigen geeft ons. Vervolgens heeft een van de lijnen die door punt P passeren en tot de hyperbolische paraboloïde een parametrische vergelijking heeft:

= + t

Om C te bepalen, vervangen we punt P in vergelijking x + y = c z, verkrijgen:

C = -1

Evenzo, maar gezien de vergelijkingen (x - y = k z) en (x + y = 1/k), hebt u de parametrische vergelijking van de lijn:

= + S met k = 1.

Kortom, de twee lijnen:

= + t y = + s

Ze zijn volledig opgenomen in de hyperbolische paraboloïde z = x² - En² Door het punt gaan (0, 1, -1).

Als een controle veronderstel t = 1 wat ons het punt (1,2, -3) geeft op de eerste regel. Je moet controleren of het ook op de paraboloïde z = x staat² - En²:

-3 = 1² - 2² = 1 - 4 = -3

Die bevestigt dat het in feite behoort tot het oppervlak van de hyperbolische paraboloïde.

De hyperbolische paraboloïde in architectuur

Figuur 6. Oceanografisch van Valencia (Spanje).Bron: Wikimedia Commons.

De hyperbolische paraboloïde is in de architectuur gebruikt door de grote avant-garde architecten, waaronder de namen van de Spaanse architect Antoni Gaudí (1852-1926) en zeer in het bijzonder de Spaanse ook de Spaanse Félix Candela (1910-1997) zijn zeer bijzonder.

Hieronder staan ​​enkele werken op basis van de hyperbolische paraboloïde:

-Kapel van de stad Cuernavaca (Mexico) Werk van architect Félix Candela.

-The Oceanographic of Valencia (Spanje), ook door Félix Candela.

Referenties

1. Encyclopedia of Mathematics. Geregeerd oppervlak. Hersteld van: encyclopediaofmath.borg
2. Llera rubén. Hyperbolisch paraboloïde. Hersteld van: Rubenllera.WordPress.com
3. Weisstein, Eric W. “Hyperbolische paraboloïde.”Van Mathworld-a Wolfram Web Resource. Hersteld van: Mathworld.Wolfraam.com
4. Wikipedia. Paraboloïde. Opgehaald uit: in.Wikipedia.com
5. Wikipedia. Paraboloïde. Hersteld van: is.Wikipedia.com
6. Wikipedia. Geregeerd oppervlak. Opgehaald uit: in.Wikipedia.com