Stelling van het bestaan ​​en uniekheid demonstratie, voorbeelden en oefeningen

Hij Bestaan ​​en uniekheid stelling stelt de noodzakelijke en voldoende voorwaarden vast voor een eerste -order differentiaalvergelijking, met een gegeven initiële toestand, om een ​​oplossing te hebben en dat deze oplossing ook de enige is. 

De stelling geeft echter geen enkele techniek of indicatie van hoe een dergelijke oplossing kan worden gevonden. Het bestaan ​​van het bestaan ​​en de uniekheid strekt zich ook uit tot differentiaalvergelijkingen van hogere orde met initiële omstandigheden, die bekend staat als Cauchy -probleem.

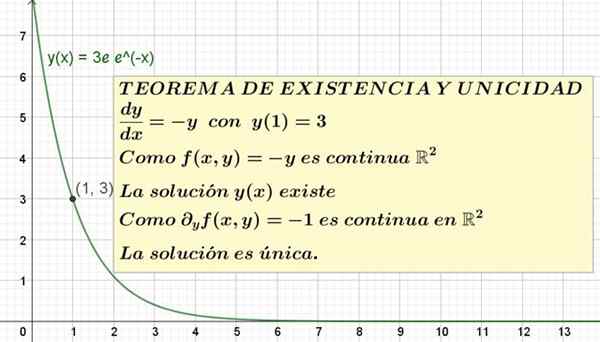
Figuur 1. Een differentiaalvergelijking met initiële toestand en de oplossing wordt getoond. Het bestaan ​​en de uniekheid stellingen garandeert dat het de enige mogelijke oplossing is.

De formele verklaring van het bestaan ​​en de unieke stelling is als volgt:

"Voor een differentiaalvergelijking en '(x) = f (x, y) met initiële toestand en (a) = b,  bestaat ten minste één oplossing in een rechthoekig gebied van het vlak XY Het punt bevat (A, b), Ja F (x, y) Het is continu in die regio. En als de gedeeltelijke afgeleide van F met betrekking tot En: G = ∂f/ ∂y Het is continu in datzelfde rechthoekige gebied, dus de oplossing is uniek in een omgeving van het punt (A, b) inhoud in de continuïteitsregio van F En G."

Het nut van deze stelling ligt eerst om te weten wat de regio's van het xy -vlak zijn waarin er een oplossing kan zijn en ook weet of de gevonden oplossing de enige mogelijke is of dat er andere zijn. 

Merk op dat in het geval dat de staat van uniek.

[TOC]

Demonstratie van het bestaan ​​van het bestaan ​​en de uniekheid

Figuur 2. Aan Charles Émile Picard (1856-1941) is een van de eerste demonstraties van het bestaan ​​en de unieke stelling geaccrediteerd. Bron: Wikimedia Commons.

Voor deze stelling zijn twee mogelijke demonstraties bekend, een daarvan is de demonstratie van Charles Émile Picard (1856-1941) en de andere is te wijten aan Giuseppe Peano (1858-1932) op basis van de werken van Augustin Louis Cauchy (1789-1857 )).

Kan u van dienst zijn: Gelijktijdige vectoren: kenmerken, voorbeelden en oefeningen

Opgemerkt moet worden dat de slimste wiskundige geesten van de negentiende eeuw deelnamen aan de demonstratie van deze stelling, dus het kan intuït zijn dat geen van beiden eenvoudig is.

Om de stelling formeel te demonstreren, is het noodzakelijk om eerst een reeks meer geavanceerde wiskundeconcepten op te zetten, zoals Lipschitz -type functies, banach -ruimtes, caratheodory en nog enkele bestaande stelling, die ontsnappen aan het doel van het artikel.

Een groot deel van de differentiaalvergelijkingen die in de natuurkunde worden behandeld, gaat om continue functies in de interessegebieden, daarom zullen we ons beperken tot het tonen van de manier waarop de stelling wordt toegepast in eenvoudige vergelijkingen.

Voorbeelden

- voorbeeld 1

Overweeg de volgende differentiaalvergelijking met een initiële toestand:

en '(x) = - y; met en (1) = 3

Is er een oplossing voor dit probleem? Is het de enige mogelijke oplossing?

Antwoorden

Ten eerste wordt het bestaan ​​van de oplossing van de differentiaalvergelijking geëvalueerd en dat deze ook voldoet aan de initiële toestand. 

In dit voorbeeld f (x, y) = - y De staat van het bestaan ​​vereist weten of  F (x, y) Het is continu in een vliegtuiggebied XY Met het coördinaatpunt x = 1, y = 3.

Maar f (x, y) = -y Het is de Gerelateerde functie, die continu is in het domein van reële getallen en bestaat in het gehele reeks reële getallen.

Daarom wordt geconcludeerd dat f (x, y) continu is in r², Dus de stelling garandeert het bestaan ​​van ten minste één oplossing.

Dit wetende, is het tijd om te beoordelen of de oplossing uniek is of dat er daarentegen meer dan één is. Hiervoor is het noodzakelijk om de gedeeltelijke afgeleide van te berekenen F Met betrekking tot de variabele En:

∂f/∂y = ∂ (-y)/∂y = -1

Dus G (x, y) = -1 wat een constante functie is, die ook wordt gedefinieerd voor alle r² En het is daar ook continu. Hieruit volgt dat het bestaan ​​en de unieke stelling van de uniekheid garandeert dat dit initiële waardeprobleem een ​​unieke oplossing heeft, hoewel het ons niet vertelt wat het is.

Kan u van dienst zijn: convexe polygoon: definitie, elementen, eigenschappen, voorbeelden

- Voorbeeld 2

Overweeg de volgende eerste -orde gewone differentiaalvergelijking met initiële toestand:

en '(x) = 2√y; en (0) = 0.

Is er een oplossing en (x) Voor dit probleem? Als dat zo is, bepaal dan of er een of meer dan één is.

Antwoord

Wij beschouwen de functie f (x, y) = 2√y. De functie F wordt alleen gedefinieerd voor Y≥0, Nou, we weten dat een negatief getal geen echte wortel heeft. Daarnaast F (x, y) Het is continu in de bovenste semiplane van r²  inclusief de X -as, dus Het bestaan ​​en de unieke stelling garanties Ten minste één oplossing in die regio.

Nu bevindt de initiële toestand x = 0, y = 0 aan de rand van het oplossingsgebied. Dan nemen we de gedeeltelijke afgeleide van f (x, y) ten opzichte van y:

∂f/∂y = 1/√y

In dit geval is de functie niet gedefinieerd voor y = 0, precies waar de initiële toestand is.

Wat vertelt ons de stelling? Het vertelt ons dat hoewel we weten dat er ten minste één oplossing is, de bovenste semiplane van de X -as inclusief de X -as, omdat de voorwaarde van uniekheid niet wordt voldaan, er geen garantie is dat er een enkele oplossing is.

Dit betekent dat er een of meer van één oplossing kan zijn in het continuïteitsgebied van F (X, Y). En zoals altijd vertelt de stelling ons niet wat er zou kunnen zijn.

Opgeloste oefeningen

- Oefening 1

Los het Cauchy -probleem op van voorbeeld 1:

en '(x) = - y; met en (1) = 3. 

Zoek de functie y (x) die voldoet aan de differentiaalvergelijking en de initiële toestand.

Oplossing

In voorbeeld 1 werd vastgesteld dat dit probleem een ​​oplossing heeft en ook uniek is. Om de oplossing te vinden, is het eerste dat moet worden opgemerkt dat het een eerste -grade differentiaalvergelijking is van scheidbare variabelen, die als volgt is geschreven:

Kan u van dienst zijn: variatiecoëfficiënt: waar is het voor, berekening, voorbeelden, oefeningen

dy /dx = - en → dy = -y dx

Verdeelt tussen en in beide leden om de variabelen te scheiden die we hebben:

dy/y = - dx

Onbepaald integraal in beide leden wordt toegepast:

∫ (1/y) dy = - ∫dx

Het oplossen van de onbepaalde integralen is:

ln (y) = -x + c

waarbij C een integratieconstante is die wordt bepaald door de initiële toestand:

ln (3) = -1 + c, dat wil zeggen dat c = 1 + ln (3)

Het vervangen van de waarde van C en reorganisatie is:

ln (y) - ln (3) = -x + 1

De volgende eigenschap van de logaritmen toepassen:

Het verschil in logaritmen is het quotiënt logaritme

De vorige uitdrukking kan zo worden herschreven:

ln (y/3) = 1 - x

De exponentiële functie wordt toegepast met beide leden om te verkrijgen:

Y / 3 = e^{(1 - x)}

Die gelijkwaardig is aan:

 y = 3e e^-X

Dit is de unieke oplossing van de vergelijking en '= -y met y (1) = 3. De grafiek van deze oplossing wordt getoond in figuur 1.

- Oefening 2

Zoek twee oplossingen voor het probleem dat wordt opgehaald in Voorbeeld 2:

en '(x) = 2√ (y); en (0) = 0.

Oplossing

Het is ook een vergelijking van afzonderlijke variabelen, die anders is geschreven, blijft bestaan:

Dy / √ (y) = 2 dx

Het nemen van de onbepaalde integraal in beide leden blijft bestaan:

2 √ (y) = 2 x + c

Zoals bekend dat Y≥0 In de oplossingsregio hebben we:

y = (x + c)² 

Maar aangezien de beginvoorwaarde x = 0, y = 0 moet worden voldaan, is de constante C nul en blijft de volgende oplossing:

en (x) = x².

Maar deze oplossing is niet uniek, de functie y (x) = 0 is ook een oplossing van het probleem dat wordt verhoogd. Het bestaan ​​en de unieke stelling van dit probleem in voorbeeld 2 had al voorspeld dat er meer dan één oplossing zou kunnen zijn.

Referenties

1. Coddington, Earl A.; Levinson, Norman (1955), Theory of gewone differentiaalvergelijkingen, New York: McGraw-Hill.
2. Encyclopedia of Mathematics. Cauchy-Lipschitz stelling. Hersteld van: encyclopediaofmath.borg
3. Lindelöf, South L'a Toepassing van de methode des A A IN INADINGEN SECUSIVESSE Aux équations Différentielles wettoraires du Premier Ordre; Compttes Rendus Hebdomadaires des Séances de l'anc Acadequie des Sciences. Vol. 116, 1894, pp. 454-457. Hersteld van: Gallic.BNF.fris.
4. Wikipedia. Picard's opeenvolgende benaderingenmethode. Hersteld van: is.Wikipedia.com
5. Wikipedia. Picard-Lindelöf Stelling. Hersteld van: is.Wikipedia.com.
6. Zill, D.1986. Elementaire differentiaalvergelijkingen met toepassingen.Prentice Hall.