Lamy's stelling
- 5078
- 867
- Aaron Okuneva

Lamy's stelling stelt vast dat wanneer een rigide lichaam in balans is en op de werking van drie coupletkrachten (krachten die zich in hetzelfde vlak bevinden), hun werklijnen op hetzelfde punt overeenkomen.
De stelling werd afgeleid door de Franse natuurkundige en religieus. Het wordt veel gebruikt om de waarde van een hoek, de actielijn van een kracht te vinden of om de driehoek van krachten te vormen.
Uitleg
De stelling stelt vast dat om de voorwaarde van het evenwicht te vervullen, de krachten moeten zijn Coplanares; dat wil zeggen, de som van de op een punt uitgeoefende krachten is nul.
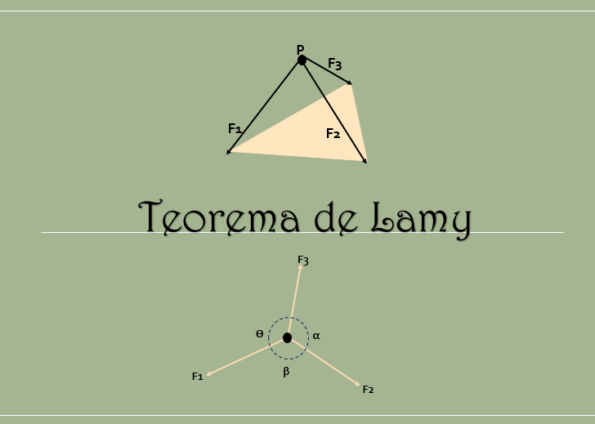
Bovendien, zoals te zien in de volgende afbeelding, wordt vervuld dat ze door het verlengen van de werkingslijnen van deze drie krachten, op hetzelfde punt eens zijn.
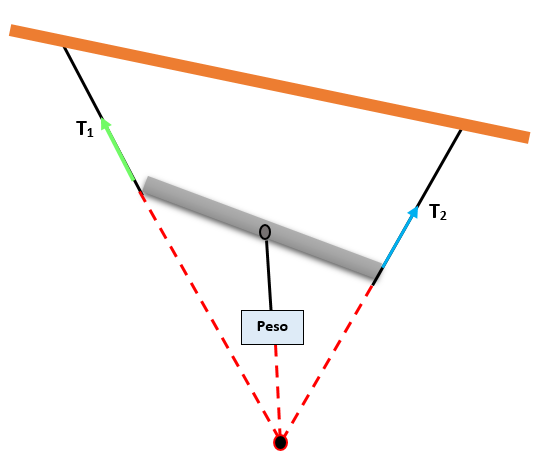
Dus als drie krachten in hetzelfde vlak en gelijktijdig zijn, zal de grootte van elke kracht evenredig zijn met de boezem van de tegenoverliggende hoek, die worden gevormd door de andere twee krachten.
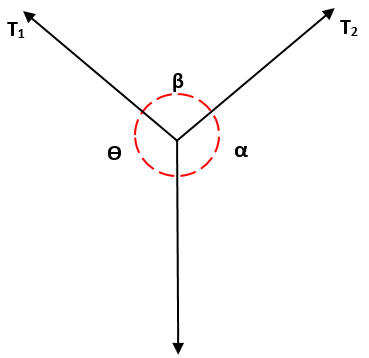
Dit moet T1, beginnend bij de borst van α, het is gelijk aan de verhouding van T2 / β, die op zijn beurt gelijk is aan de verhouding van T3 / ɵ, dat wil zeggen:
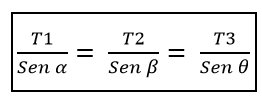
Van daaruit volgt dat de modules van deze drie krachten hetzelfde moeten zijn als de hoeken die elk paar krachten vormen gelijk zijn aan 120º.
Er is de mogelijkheid dat een van de hoeken stomp is (meet tussen 900 en 1800)). In dat geval zal de borst van die hoek gelijk zijn aan de boezem van de aanvullende hoek (in zijn paar meet het 1800)).
Kan u van dienst zijn: wetten van exponentenOefening opgelost
Er is een systeem gevormd door twee J- en K -blokken, die aan verschillende snaren hangen die hoeken vormen ten opzichte van de horizontale, zoals weergegeven in de figuur. Het systeem is in evenwicht en het J -blok weegt 240 n. Bepaal het gewicht van blok k.
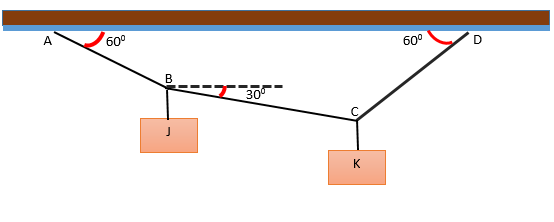
Oplossing
Door het principe van werking en reactie zullen de spanningen die in blokken 1 en 2 worden uitgeoefend gelijk zijn aan het gewicht hiervan.
Nu is een vrij lichaamsdiagram voor elk blok gebouwd en bepaal zo de hoeken die het systeem vormen.
Het is bekend dat het touw dat naar A gaat tot B, een invalshoek van 30 heeft0 , zodat de hoek die het aanvult, gelijk is aan 600 . Op die manier bereik je 900.
Aan de andere kant, waar punt A zich bevindt, is er een hoek van 600 met betrekking tot de horizontale; De hoek tussen verticaal en tNAAR Het zal = 180 zijn0 - 600 - 900 = 300.
Aldus wordt verkregen dat de hoek tussen AB en BC = (300 + 900 + 300) en (600 + 900 + 60) = 1500 en 2100. Bij het toetreden is het geverifieerd dat de totale hoek 360 is0.
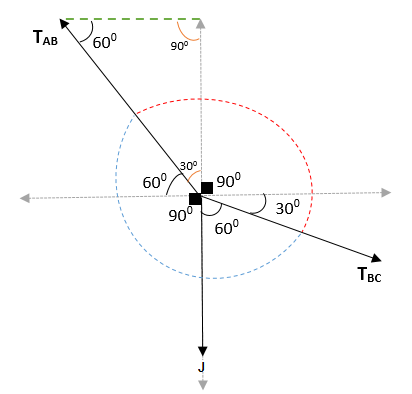
Lamy's stelling toepassen die u moet:
TBC/ Sin 1500 = PNAAR/ Sin 1500
TBC = PNAAR
TBC = 240N.
Op punt C, waar is het blok, de hoek tussen het horizontale en het BC -touw is 30 is 300, Dus de complementaire hoek is gelijk aan 600.
Aan de andere kant is er een hoek van 600 op het CD -punt; De hoek tussen verticaal en tC Het zal = 180 zijn0 - 900 - 600 = 300.
Kan u van dienst zijn: Coplanares -punten: vergelijking, voorbeeld en opgeloste oefeningenAldus wordt verkregen dat de hoek in blok K = (30 is0 + 600))
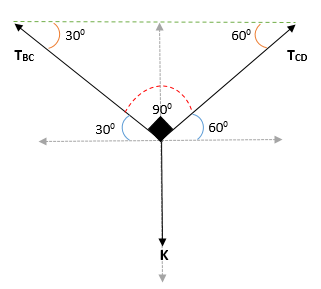
Lamy's stelling toepassen op punt C:
TBC/ Sin 1500 = B / sin 900
Q = TBC * Sen 900 / Sin 1500
Q = 240 N * 1/0.5
Q = 480 n.
Referenties
- Ferdinand P. Bier, e. R. (2013). Mechanica voor ingenieurs, statisch. McGraw-Hill Inter-American.
- Francisco Español, J. C. (2015). Lineaire algebra -problemen opgelost. Paraninfo Editions, s.NAAR.
- Graham, J. (2005). Kracht en beweging. Houchton Mifflin Harcourt.
- Harpe, p. D. (2000). Onderwerpen in de geometrische groepstheorie. Universiteit van Chicago Press.
- P. Een tpler y, g. M. (2005). Natuurkunde voor wetenschap en technologie. Deel I. Barcelona: Keer je terug.NAAR.

