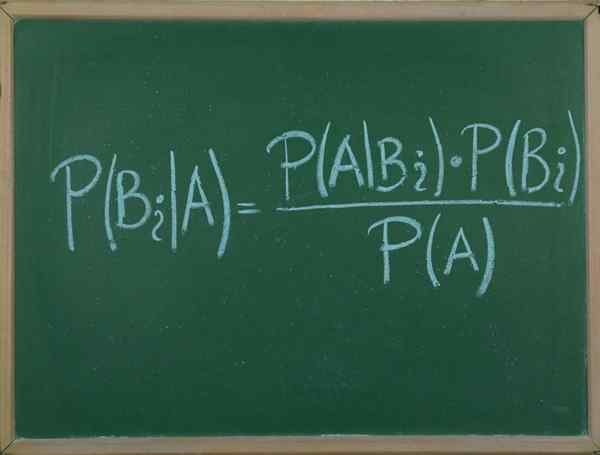Bayes -stelling
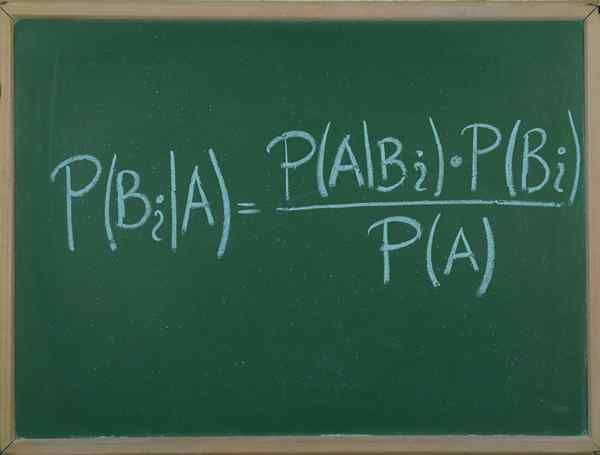
- 2638
- 325
- Alton D'Amore
We leggen uit wat de stelling van Bayes is, de toepassingen ervan en we zetten oefeningen opgelost op
Wat is de stelling van Bayes?
Hij Bayes -stelling Het is een procedure waarmee we de voorwaardelijke waarschijnlijkheid van een willekeurige gebeurtenis A DICE B kunnen uiten, in termen van de waarschijnlijkheidsverdeling van gebeurtenis B en de waarschijnlijkheidsverdeling van alleen tot.
Deze stelling is erg nuttig, want dankzij het kunnen we de waarschijnlijkheid relateren dat een gebeurtenis A toevallig weet dat B gebeurde, met de waarschijnlijkheid dat het tegenovergestelde optreedt, dat wil zeggen dat het voorkomt.
De stelling van Bayes was een zilveren propositie van dominee Thomas Bayes, een achttiende -eeuwse Engelse theoloog die ook een wiskundige was. Hij was de auteur van verschillende banen in theologie, maar momenteel staat hij bekend om een paar wiskundige verdragen, waaronder de stelling van Bayes die al als hoofdresultaat wordt genoemd.
Bayes behandelde deze stelling in een werk getiteld "Een essay voor het oplossen van een probleem in de doctrine van kansen" (een essay om een probleem op te lossen in de doctrine van de mogelijkheden), gepubliceerd in 1763, en waarop grote studies met toepassingen hebben ontwikkeld met toepassingen met toepassingen op verschillende kennisgebieden.
Uitleg
Ten eerste, voor een grotere compressie van deze stelling zijn enkele fundamentele noties van waarschijnlijkheidstheorie noodzakelijk, met name de vermenigvuldigingstheorie voor voorwaardelijke waarschijnlijkheid, die dat vaststelt
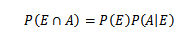
Voor e en aan willekeurige gebeurtenissen van een voorbeeldruimte s.
En de definitie van partities, die ons vertelt dat we dat hebben gedaan1 ,NAAR2,… , NAARN gebeurtenissen van een voorbeeldruimte, deze vormen een partitie van s, als de aJe Ze sluiten elkaar uit en hun vakbond is S.
Kan u van dienst zijn: waar zijn de cijfers voor? Het 8 belangrijkste gebruikAls u dit hebt, zij het een ander evenement. Dus we kunnen B zien
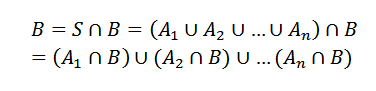
Waar eenJe doorsneden met B zijn wederzijds exclusieve gebeurtenissen.
En bijgevolg,
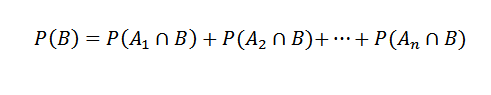
Vervolgens toepassen van de stelling van de vermenigvuldiging
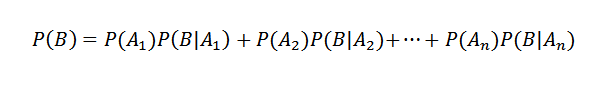
Aan de andere kant wordt de voorwaardelijke waarschijnlijkheid van AI B gedefinieerd door
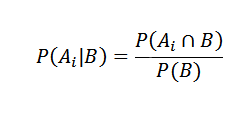
Correct vervangen we hebben dat voor elke ik
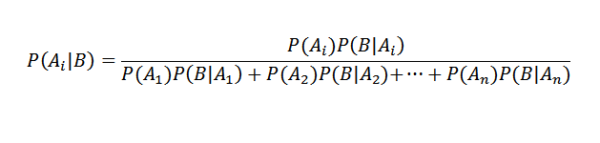
Bayes Stelling Toepassingen
Dankzij dit resultaat zijn onderzoeksgroepen en diverse bedrijven erin geslaagd om de systemen te verbeteren die op kennis zijn gebaseerd.
Ziektestudie
In de studie van ziekten kan de stelling van Bayes bijvoorbeeld helpen de kans te onderscheiden dat een ziekte zal worden gevonden in een groep mensen met een bepaald kenmerk, als gegevens de wereldwijde percentages van de ziekte en de overheersing van genoemde kenmerken in beide in beide Gezonde en zieke mensen.
Software ontwikkeling
Aan de andere kant heeft het in de wereld van hoge technologieën grote bedrijven beïnvloed die, dankzij dit resultaat, software "op basis van kennis" hebben ontwikkeld ".
Als dagelijks voorbeeld hebben we de Microsoft Office Assistant. De stelling van Bayes helpt software om de problemen te evalueren die de gebruiker presenteert en te bepalen welk advies hij moet bieden en zo een betere service kan bieden volgens de gewoonten van de gebruiker.
Opgemerkt moet worden dat deze formule tot de laatste tijd werd genegeerd, dit is vooral omdat wanneer dit resultaat 200 jaar geleden werd ontwikkeld, er weinig praktisch voor hen was. In onze tijd hebben wetenschappers dankzij de grote technologische vooruitgang echter manieren bereikt om dit resultaat in de praktijk te brengen.
Opgeloste oefeningen
Oefening 1
Een mobiele telefoonbedrijf heeft twee A- en B -machines. 54% van de mobiele telefoons wordt gemaakt door machine A en de rest door machine B. Niet alle mobiele telefoons zijn in goede staat.
Kan u van dienst zijn: factorisatieHet aandeel defecte mobiele telefoons gemaakt door A is 0.2 en voor B is 0.5. Wat is de kans dat een mobiele telefoon van die fabriek defect is? Wat is de kans dat, wetende dat een mobiele telefoon defect is, van de machine komt naar?
Oplossing
Hier heb je een experiment dat in twee delen wordt uitgevoerd; In het eerste deel komen de gebeurtenissen voor:
Naar: mobiele telefoon gemaakt door machine a.
B: mobiele telefoon gemaakt door machine B.
Omdat machine A 54% van de mobiele telefoons produceert en de rest wordt geproduceerd door machine B, moet machine B 46% van de mobiele telefoons produceren. De kansen van deze gebeurtenissen worden gegeven, namelijk:
P (a) = 0,54.
P (B) = 0,46.
De gebeurtenissen in het tweede deel van het experiment zijn:
D: Defecte mobiele telefoon.
E: Niet -definitieve cel.
Zoals vermeld in de verklaring, zijn de waarschijnlijkheden van deze gebeurtenissen afhankelijk van het resultaat dat in het eerste deel is verkregen:
P (d | a) = 0,2.
P (D | B) = 0,5.
Met behulp van deze waarden kunt u ook de kansen van de accessoires van deze gebeurtenissen bepalen, dat wil zeggen:
P (e | a) = 1 - p (d | a)
= 1 - 0,2
= 0,8
En
P (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Nu kan de D -gebeurtenis als volgt worden geschreven:
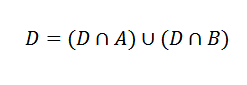 Deze gebeurtenissen sluiten elkaar uit.
Deze gebeurtenissen sluiten elkaar uit.
Het gebruik van de vermenigvuldigingstoestand voor voorwaardelijke waarschijnlijkheid is:
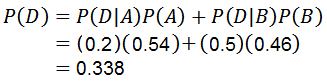
Waarmee de eerste vraag wordt beantwoord.
Nu moeten we alleen p (a | d) berekenen, waarvoor de stelling van Bayes wordt toegepast:
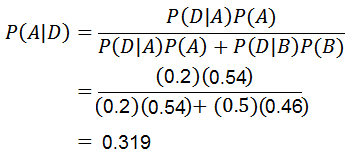
Dankzij de stelling van Bayes kan worden bevestigd dat de kans dat een mobiele telefoon is gemaakt door machine A, wetende dat de mobiele telefoon defect is, is 0.319.
Kan je van dienst zijn: IcosagonoOefening 2
Drie dozen bevatten zwarte en zwarte ballen. De samenstelling van elk van hen is als volgt: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
Een willekeurig gekozen een van de dozen en er wordt een willekeurige bal uit geëxtraheerd die wit blijkt te zijn. Wat is de doos met het meest waarschijnlijk gekozen?
Oplossing
Via U1, U2 en U3 zullen we ook de gekozen doos vertegenwoordigen.
Deze gebeurtenissen vormen een partitie van S en het is geverifieerd dat P (U1) = P (U2) = P (U3) = 1/3 omdat de keuze van de doos willekeurig is.
Als b = de geëxtraheerde bal wit is, hebben we p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
Wat we willen verkrijgen is de kans dat de bal uit de IU -doos is gehaald wetende dat deze bal wit was, dat wil zeggen p (ui | b), en zien welke van de drie waarden de hoogste was om te weten welke van welke doos meer kans heeft op extractie van de witte bal.
Bayes 'stelling toepassen op de eerste van de dozen:
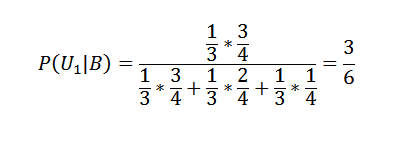
En voor de andere twee:
P (U2 | B) = 2/6 en P (U3 | B) = 1/6.
Dan is de eerste van de dozen degene die een grotere kans heeft om te zijn gekozen voor de extractie van de witte bal.