Telescopische zomer hoe het wordt opgelost en opgeloste oefeningen

De sommatie Telescopisch Het is een tak van bewerkingen met numerieke serie. Behandelt de samenvattingen van elementen van een initiële waarde tot "n" van uitdrukkingen waarvan het argument te wijten is aan een van de volgende patronen:

(F_X - F_x+1); F_x+1  - F_X))

Waar de samenvattende uitdrukking als volgt wordt gedefinieerd: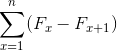

Ook:

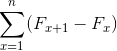
Bron: Pixabay.com

Ze vertegenwoordigen een som van elementen die, bij het ontwikkelen, onderworpen zijn aan annulering van tegengestelde termen. Waardoor de volgende gelijkheid voor telescopische summaties wordt veroorzaakt:

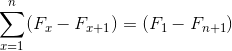
De naam komt van de relatie met het uiterlijk van een klassieke telescoop, die kan worden gevouwen en geïmplementeerd, waardoor de dimensie aanzienlijk wordt veranderd. Evenzo kunnen telescopische samenvattingen, die in hun aard oneindig zijn, worden samengevat in vereenvoudigde expressie:

F₁ - F_N+1

[TOC]

Demonstratie

Bij het ontwikkelen van de som van termen is de eliminatie van factoren vrij duidelijk. Waar voor elk van de gevallen tegengestelde elementen verschijnen in de volgende iteratie.

Het eerste geval zal als voorbeeld worden opgevat, (f_X - F_x+1), omdat het proces homoloog werkt aan (f_x+1-F_X)).

Het ontwikkelen van de eerste 3 waarden 1, 2, 3 De vereenvoudiging neiging wordt waargenomen

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Waar door de som van de beschreven elementen uit te drukken:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Opgemerkt wordt dat de voorwaarden F₂ en f₃ Ze worden beschreven met hun tegenstellingen, wat hun vereenvoudiging onvermijdelijk maakt. Op dezelfde manier wordt opgemerkt dat de termen f₁ en f₄ blijven.

Als de som is gemaakt van x = 1 tot x = 3, betekent dit dat element f₄ komt overeen met de generieke term f_N+1.

Dus het aantonen van gelijkheid:

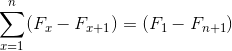
Hoe wordt het opgelost?

Het doel van telescopische summaties is om werk te vergemakkelijken, zodat het niet nodig is om een ​​oneindige hoeveelheid termen te ontwikkelen of een te lange keten te vereenvoudigen.

Kan u van dienst zijn: Trachtenberg -methode: wat is het, voorbeelden

Voor resolutie is het alleen nodig om de voorwaarden F te evalueren₁ en f_N+1. Deze eenvoudige substituties vormen het eindresultaat van de som.

De totaliteit van de voorwaarden zal niet worden uitgedrukt en noodzakelijk worden voor de demonstratie van het resultaat, maar niet voor het normale berekeningsproces.

Het belangrijkste is om de convergentie van de numerieke serie op te merken. Soms wordt het argument van de som niet op een telescopische manier uitgedrukt. In deze gevallen komt de implementatie van alternatieve factorisatiemethoden veel voor.

De karakteristieke factorisatiemethode in telescopische samenvattingen is die van eenvoudige breuken. Dit gebeurt wanneer een originele fractie ontleedt in een som van verschillende fracties, waarbij het telescopische patroon kan worden waargenomen (f_X - F_x+1) of (f_x+1  - F_X)).

Ontleding in eenvoudige breuken

Om de convergentie van numerieke series te verifiëren, is het heel gebruikelijk om rationele uitdrukkingen te transformeren met de eenvoudige breukenmethode. Het doel is om het argument te modelleren tot de vorm van een telescopische sommatie.

De volgende gelijkheid vertegenwoordigt bijvoorbeeld een ontleding in eenvoudige breuken:

Bij het ontwikkelen van de numerieke serie en het toepassen van de overeenkomstige eigenschappen neemt de uitdrukking als volgt:

Waar de telescopische vorm kan worden gezien (f_X - F_x+1)).

De procedure is vrij intuïtief en bestaat uit het vinden van de waarden van de teller die, zonder de gelijkheid te breken, het mogelijk maakt om de producten te scheiden die in de noemer zijn. De vergelijkingen die zich voordoen bij de bepaling van deze waarden, worden verhoogd volgens vergelijkingen tussen beide zijden van gelijkheid.

Deze procedure wordt stap voor stap waargenomen bij de ontwikkeling van Oefening 2.

Kan u van dienst zijn: 6 leuke wiskundige raadsels voor kinderen

Geschiedenis

Het is vrij onzeker om het historische moment te kunnen definiëren waarop de telescopische samenvoegingen werden gepresenteerd. De implementatie ervan begint echter te worden gezien in de zeventiende eeuw, in numerieke series studies uitgevoerd door Leibniz en Huygens.

Beide wiskundigen beginnen bij het verkennen van de samenvatting van driehoekige aantallen trends op te merken in de convergentie van bepaalde reeks opeenvolgende elementen. Maar nog interessanter is het begin van de modellering van deze uitdrukkingen, in elementen die niet noodzakelijkerwijs gebeuren.

In feite werd de uitdrukking die eerder werd gebruikt om te verwijzen naar eenvoudige breuken:

Het werd gepresenteerd door Huygens en noemde onmiddellijk de aandacht van Leibniz. Die na verloop van tijd de convergentie zou kunnen observeren om te waarde 2. Zonder het te weten, implementeerde het de telescopische sommatie.

Opdrachten

Oefening 1

Bepaal welke term het volgende bedrag convergeert:

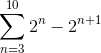
Wanneer de som handmatig wordt ontwikkeld, wordt het volgende patroon waargenomen:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶)… (2¹⁰ - 2^elf))

Waar de factoren van 2⁴ maximaal 2¹⁰ Ze presenteren positieve en negatieve delen, waardoor hun annulering duidelijk wordt. Dan zijn de enige factoren die niet worden vereenvoudigd de eerste “2³"En de laatste" 2^elf".

Op deze manier wordt bij het implementeren van de telescopische samenvattende criteria verkregen:

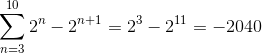
Oefening 2

Transformeer het argument in een telescopisch type som en definieer de convergentie van de serie:

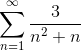
Zoals aangegeven in de verklaring, zal het eerste zijn om in eenvoudige breuken te ontleden, om het argument te heroverwegen en in een telescopische vorm uit te drukken.

2 breuken waarvan de noemers respectievelijk "n" en "n+1" zijn, moeten worden gevonden, waarbij de hieronder gebruikte methode de waarden van de teller moet bereiken die aan gelijkheid voldoen.

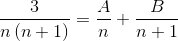
De waarden van A en B zijn gedefinieerd. Eerste som van breuken wordt gemaakt.

Kan u van dienst zijn: 60 delers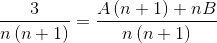

Vervolgens worden noemers vereenvoudigd en wordt een lineaire vergelijking vastgesteld.

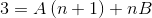
In de volgende stap wordt de uitdrukking van rechts gewerkt, totdat een patroon vergelijkbaar is met de "3" aan de linkerkant.

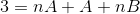
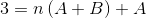
Om de te gebruiken vergelijkingen te definiëren, moeten de resultaten van beide zijden van gelijkheid worden vergeleken. Dat wil zeggen, er worden geen variabele N -waarden aan de linkerkant waargenomen, op deze manier zal A +B gelijk moeten zijn aan nul.

A + b = 0; A = -b

Aan de andere kant moet de constante waarde gelijk zijn aan constante waarde 3.

A = 3

Daarom.

A = 3 en B = -3

De waarden van de teller al gedefinieerd voor eenvoudige breuken, de som is heroverwegen.

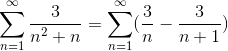
Waar de generieke vorm van telescopische sommatie al is bereikt. De telescopische serie is ontwikkeld.

Waar door het delen door een zeer groot aantal het resultaat meer en meer bij benadering zal zijn, waarbij de convergentie van de serie om waarde 3 wordt geobserveerd 3.

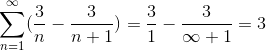
Dit type series kon niet met andere woorden worden opgelost, vanwege de oneindige hoeveelheid iteraties die het probleem definiëren. Deze methode kadert echter, samen met vele anderen, de tak van de studie van de numerieke serie, waarvan de doelstelling is om de convergentiewaarden te bepalen of de divergentie van deze serie te definiëren.

Referenties

1. Infinitesimale berekeningslessen. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Editum, 1994.
2. Uitgebreide berekening: opvolgingen en reeks functies. Antonio Rivera Figueroa. Patria Editorial Group, 21 oktober. 2014.
3. Een cursus calculus en echte analyse. Sudhir r. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 juni. 2006.
4. Oneindige serie. Tomlinson Fort. The Clarendon Press, 1930.
5. Elementen van de theorie van oneindige processies. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorpan, 1923.