Octaal systeem

Wat is een octaal systeem?

Hij Octaal systeem Het is een basisnummeringssysteem acht (8); Dat wil zeggen, het bestaat uit acht cijfers, die zijn: 0, 1, 2, 3, 4, 5, 6 en 7. Daarom kan elk cijfer van een octaal nummer elke waarde hebben van 0 tot 7. Octale nummers worden gevormd uit binaire getallen.

Dit komt omdat de basis een exacte kracht is van twee (2). Dat wil zeggen, de getallen die tot het octale systeem behoren, worden gevormd wanneer ze worden gegroepeerd in drie opeenvolgende cijfers, van rechts naar links besteld, waardoor hun decimale waarde wordt verkregen.

Geschiedenis van het octale systeem

Het octale systeem heeft zijn oorsprong in de oudheid, toen mensen hun handen gebruikten om acht om acht dieren te tellen.

Om bijvoorbeeld het aantal koeien in een stal te tellen, begon de rechterhand de duim met de pink te hebben; Om het tweede dier te tellen, kwam de duim samen met de wijsvinger, enzovoort met de resterende vingers van elke hand, totdat deze 8 voltooid.

Er is de mogelijkheid dat het octale nummeringssysteem vóór het decimaal de interdigitale ruimtes kan tellen; dat wil zeggen, vertel alle vingers behalve de duimen.

Vervolgens werd het octale nummeringssysteem vastgesteld, dat afkomstig was van het binaire systeem, omdat het veel cijfers nodig heeft om slechts één nummer weer te geven; Vanaf dat moment werden octal- en zeshoekige systemen gemaakt, die niet zoveel cijfers vereisen en dat kan gemakkelijk converteren naar het binaire systeem.

Octale nummeringssysteem

Het octale systeem bestaat uit acht cijfers variërend van 0 tot 7. Deze hebben dezelfde waarde als in het geval van het decimale systeem, maar hun relatieve waarde verandert afhankelijk van de positie die deze bezetten. De waarde van elke positie wordt gegeven door de basisbevoegdheden 8.

Het kan u van dienst zijn: regel T: kenmerken, zodat het voorbeelden zijn

De posities van de cijfers in een octaal nummer hebben de volgende pesos:

8⁴, 8³, 8², 8¹, 8⁰, Octal Point, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Het belangrijkste octale cijfer is 7; Op deze manier neemt wanneer in dit systeem een ​​positie van een cijfer van 0 tot 7 toe te tellen toeneemt. Wanneer het 7 bereikt, wordt het gerecycled op 0 voor de volgende telling; Dit verhoogt de volgende cijferspositie. Om bijvoorbeeld sequenties te tellen, zal het in het octale systeem zijn:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Er is een fundamentele stelling die wordt toegepast op het octale systeem en wordt als volgt uitgedrukt:

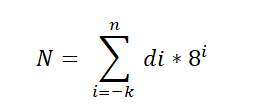
In deze uitdrukking vertegenwoordigt DI het cijfer vermenigvuldigd met de basis 8 -kracht, die de positionele waarde van elk cijfer aangeeft, op dezelfde manier waarop het in het decimale systeem wordt geordend,.

U hebt bijvoorbeeld het nummer 543.2. Om het naar het octale systeem te brengen, ontleedt het als volgt:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0.125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_D

Op die manier heb je 543.2_Q = 354.25_D. Het subscript dat aangeeft dat het een octaal nummer is dat ook kan worden weergegeven door nummer 8; en subscript D verwijst naar het decimale nummer, dat ook kan worden weergegeven met nummer 10.

Octale systeemconversie naar decimalen

Om een ​​octaal systeemnummer om te zetten in het equivalent in het decimale systeem, moet elk octaal cijfer worden vermenigvuldigd met zijn positionele waarde, beginnend bij rechts.

voorbeeld 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Kan u van dienst zijn: wiskundige gelijkheid

Voorbeeld 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0.125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23,125₁₀

Decimale systeemconversie naar octal

Een decimaal gehele getal kan worden omgezet in een octaal nummer met behulp van de herhaalde divisiemethode, waarbij het decimale geheel getal wordt gedeeld door 8 totdat het quotiënt gelijk is aan 0, en de verspilling van elke divisie zal het octale nummer vertegenwoordigen.

Het afval wordt geordend van het laatste tot de eerste; dat wil zeggen, het eerste residu zal het minst significante cijfer van het octale aantal zijn. Op deze manier zal het belangrijkste cijfer het laatste residu zijn.

Voorbeeld

Octaal van het decimale nummer 266₁₀

- Decimaal nummer 266 wordt gedeeld door 8 = 266/8 = 33 + 2 residu.

- Dan wordt de 33 gedeeld door 8 = 33/8 = 4 + 1 residu.

- 4 wordt gedeeld door 8 = 4/8 = 0 + 4 residu.

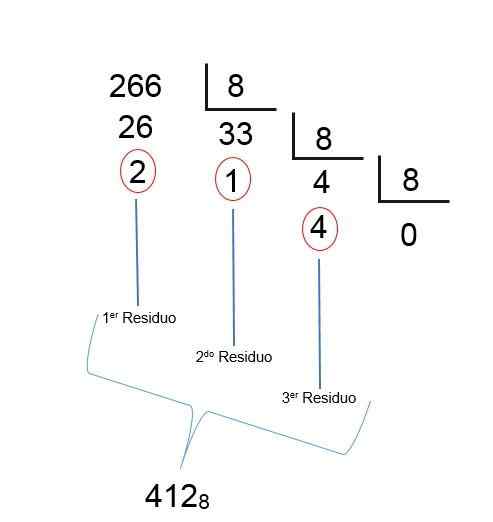
Net als bij de laatste divisie wordt een quotiënt minder dan 1 verkregen, betekent dit dat het resultaat is gevonden; Alleen de overblijfselen moeten omgekeerd worden besteld, zodat het octale aantal decimaal 266 412 is, zoals te zien is in de volgende afbeelding:

Binaire octale systeemconversie

De conversie van het octale naar binaire systeem wordt uitgevoerd bij het omzetten van het octale cijfer naar zijn equivalente binaire cijfer, gevormd door drie cijfers. Er is een tabel die laat zien hoe de acht mogelijke cijfers worden:

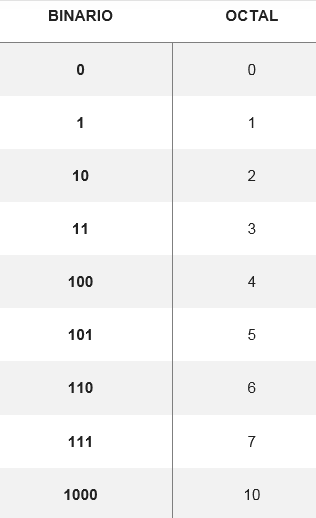
Uit deze conversies kunt u een willekeurig aantal van het octale systeem wijzigen in binair, zoals om nummer 572 te converteren₈ Uw equivalenten worden in de tabel gezocht. Je moet dus:

5₈ = 101

7₈= 111

2₈ = 10

Daarom 572₈ equivalent in het binaire systeem tot 10111110.

Binair systeem tot octale conversie

Het conversieproces van integrale getallen naar octale gehele getallen is de omgekeerde bewerking van het vorige proces.

Kan u van dienst zijn: wat zijn de elementen van een hoek?

Dat wil zeggen, de binaire nummerbits zijn gegroepeerd in twee groepen van drie bits, beginnend van rechts naar links. Vervolgens wordt binaire naar octale conversie gemaakt met de vorige tabel.

In sommige gevallen zal het binaire nummer geen groepen van 3 bits hebben; Om het te voltooien, worden een of twee nullen links van de eerste groep toegevoegd.

Bijvoorbeeld om het binaire nummer 11010110 te wijzigen in Octal, wordt het volgende gedaan:

- Groepen van 3 bits worden gevormd vanaf de rechterkant (laatste bit):

11010110

- Omdat de eerste groep onvolledig is, wordt een nul aan de linkerkant toegevoegd:

011010110

- De conversie is gemaakt van de tabel:

011 = 3

010 = 2

110 = 6

Op deze manier is binair getal 011010110 gelijk aan 326₈.

Conversie van het octale systeem naar hexadecimaal en vice versa

Om een ​​octaal nummer te wijzigen in het hexadecimale of hexadecimale in octale systeem, is het noodzakelijk dat het nummer eerst binair is, en vervolgens naar het gewenste systeem.

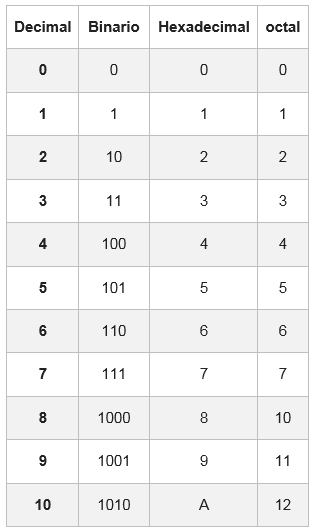
Hiervoor is er een tabel waar elk hexadecimaal cijfer wordt weergegeven met zijn equivalentie in het binaire systeem, samengesteld uit vier cijfers.

In sommige gevallen zal het binaire nummer geen groepen van 4 bits hebben; Om het te voltooien, worden een of twee nullen links van de eerste groep toegevoegd

Voorbeeld

Converteer het 1646 octale nummer in een hexadecimaal nummer:

- Het octale tot binair getal wordt

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Dus 1646₈ = 1110100110.

- Om van binair naar hexadecimaal te converteren, worden ze eerst besteld in een groep van 4 bits, beginnend van rechts naar links:

11 1010 0110

- De eerste groep is voltooid met nullen, zodat deze 4 bits kan hebben:

0011 1010 0110

- Hexadecimale binaire systeemconversie wordt gemaakt. De equivalenties worden vervangen door middel van de tabel:

0011 = 3

1010 = A

0110 = 6

Op deze manier is het 1646 octale nummer gelijk aan 3A6 in het hexadecimale systeem.