Tweede wet van thermodynamica -formules, vergelijkingen, voorbeelden

De Tweede wet van de thermodynamica heeft verschillende vormen van expressie. Een van hen stelt dat geen enkele thermische machine in staat is om alle energie die het absorbeert volledig om te zetten in bruikbaar werk (Kelvin-Planck-formulering). Een andere manier om te zeggen dat het is om te zeggen dat echte processen zich voordoen in zo'n zin dat de kwaliteit van energie lager is omdat de Entropie Het neemt de neiging toe.

Deze wet, ook bekend als het tweede principe van de thermodynamica, is op verschillende manieren uitgedrukt met het verstrijken van de tijd, van het begin van de 19e eeuw tot heden, hoewel de oorsprong ervan dateert uit de oprichting van de eerste stoommachines in Engeland, aan het begin van de 18e eeuw.

Figuur 1. Bij het bouwen van de bouwblokken op de vloer zou het zeer verrassend zijn om te worden besteld. Bron: Pixabay.

Maar hoewel het op veel manieren wordt uitgedrukt, in al het idee dat materie de neiging heeft om te wanorderen en dat er geen proces van 100%is, omdat er altijd verliezen zullen bestaan, zal altijd bestaan.

Alle thermodynamische systemen houden zich aan dit principe, beginnend met het universum zelf tot het kopje ochtendkoffie die rustig op de tafel wachtend warmte uitwisselen met de omgeving.

De koffie afkoelt naarmate de tijd verstrijkt, totdat deze in het thermische evenwicht is met de omgeving, dus het zou zeer verrassend zijn als op een dag het tegenovergestelde zou gebeuren en de sfeer zou afkoelen terwijl de koffie voor zichzelf zou opwarmen. Het is onwaarschijnlijk dat het zal gebeuren, sommigen zullen dat onmogelijk zeggen, maar het is voldoende om zich voor te stellen dat het een idee heeft van het gevoel waarin dingen spontaan gebeuren.

In een ander voorbeeld, als we een boek over het oppervlak van een tafel schuiven, zal het uiteindelijk stoppen, omdat de kinetische energie verloren gaat in de vorm van warmte als gevolg van wrijving.

De eerste en tweede wet van de thermodynamica werd rond 1850 opgericht, dankzij wetenschappers zoals Lord Kelvin -creator van de term "thermodynamica" -, William Rankine -auteur van de eerste formele tekst van thermodynamica -en Rudolph Clausius.

[TOC]

Formules en vergelijkingen

Entropie -minder dan het begin -helpt ons het gevoel waarin dingen gebeuren. Laten we teruggaan naar het voorbeeld van de lichamen in thermisch contact.

Wanneer twee objecten bij verschillende temperaturen in contact worden gebracht en uiteindelijk na een tijdje ze de thermische balans bereiken, worden ze erdoor aangedreven door het feit dat de entropie zijn maximum bereikt, wanneer de temperatuur van beide hetzelfde is.

Entropie aangeven als S, De verandering in entropie Δs van een systeem wordt gegeven door:

Q is de warmte in joules en t is de temperatuur in kelvins. In het internationale systeem van SI -eenheden wordt entropie gegeven in Joules/Kelvins of J/K.

De verandering van entropie Δs Het geeft de mate van wanorde aan in een systeem, maar er is een beperking in het gebruik van deze vergelijking: het is alleen van toepassing op omkeerbare processen, dat wil zeggen die waarin het systeem kan terugkeren naar zijn oorspronkelijke status zonder een teken van wat te achterlaten gebeurd-.

In onomkeerbare processen wordt de tweede wet van de thermodynamica als volgt gemanifesteerd:

Kan u van dienst zijn: Reynolds -nummer: waar is het voor, hoe het wordt berekend, oefeningen

Ongelijkheid ontstaat omdat in onomkeerbare processen entropie altijd toeneemt.

Omkeerbare en onomkeerbare processen

De koffiekopje koelt altijd en is een goed voorbeeld van een onomkeerbaar proces, omdat het altijd in één richting plaatsvindt. Als er room wordt toegevoegd aan de koffie en roer, wordt een zeer aangename combinatie verkregen, maar ongeacht hoe roeren weer, de koffie en room zullen niet weer zijn, omdat roeren onomkeerbaar is.

Figuur 2. Cup -breuk is een onomkeerbaar proces. Bron: Pixabay.

Hoewel de meeste dagelijkse processen onomkeerbaar zijn, zijn sommige dat wel bijna Omkeerbaar. Omkeerbaarheid is een idealisatie. Om te worden uitgevoerd, moet het systeem heel langzaam veranderen, zodat het op elk punt altijd in balans is. Op deze manier is het mogelijk om het terug te brengen naar een vorige staat zonder een stempel te laten.

De processen die vrij dicht bij dit ideaal liggen, zijn efficiënter, omdat ze een grotere hoeveelheid werk leveren met minder energieverbruik.

De wrijvingskracht is verantwoordelijk voor een groot deel van de onomkeerbaarheid, omdat de door het gegenereerde hitte niet het type energie is dat wordt gevraagd. In het boek dat over de tafel glijdt, is warmte door wrijving energie die niet wordt hersteld.

Hoewel het boek terugkeert naar zijn oorspronkelijke positie, zal de tabel hot zijn geweest als een voetafdruk om eraan te komen en erop te gaan.

Observeer nu een gloeilamp: het grootste deel van het werk dat wordt gedaan door de stroom die de gloeidraad kruist, wordt verspild aan warmte door joule -effect. Slechts een klein percentage wordt gebruikt om licht uit te stoten. In beide processen (boek en bol) is de entropie van het systeem toegenomen.

Toepassingen

Een ideale motor is degene die is gebouwd door omkeerbare processen en wrijving mist die energieverspilling veroorzaakt, draaiend bijna Alle thermische energie in bruikbaar werk.

We benadrukken het woord bijna, want zelfs de ideale motor, die Carnot is, heeft 100% efficiëntie. De tweede wet van de thermodynamica is niet op deze manier.

Carnot -motor

Carnot's motor is de meest efficiënte motor die kan worden bedacht. Het werkt tussen twee temperatuurafzettingen in twee isothermische processen - bij constante temperatuur - en twee adiabatische processen - zonder thermische energieoverdracht-.

De grafieken die PV -drukdiagrammen worden genoemd - Volume- Verduidelijk de situatie:

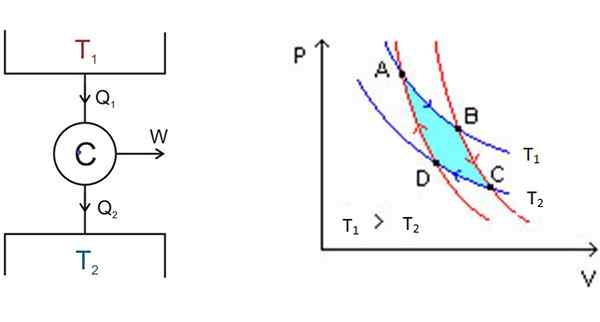figuur 3. Links links het Carnot-motorschema en rechts het P-V-diagram. Bron: Wikimedia Commons.

Links is in figuur 3 het Carnot C -motorschema, dat warmte Q nodigt Q₁ van de afzetting bij temperatuur T₁, zet die warmte om in het werk w en geef dat afval₂ tot de koudste afzetting, die op temperatuur T is₂.

Beginnend met A, breidt het systeem uit totdat het B bereikt, waardoor warmte wordt opgenomen tot vaste temperatuur T₁. In B begint het systeem een ​​adiabatische expansie waarin hitte niet wordt gewonnen of verloren, om C te bereiken.

In C begint een ander isothermproces: om warmte te geven aan de andere koudere thermische afzetting die op T is₂. Naarmate dit gebeurt, wordt het systeem gecomprimeerd en wordt punt D bereikt. Er begint een tweede adiabatisch proces om terug te keren naar het startpunt naar. Op deze manier is een cyclus voltooid.

Het kan u van dienst zijn: warmteoverdracht door te rijden (met voorbeelden)

De efficiëntie van Carnot hangt af van de temperaturen in Kelvin op de twee thermische afzettingen:

Maximale efficiëntie = (q_Ingang - Q_Uitgang) /Q_Ingang = 1 - (T₂/T₁))

De stelling van Carnot stelt dat dit de meest efficiënte thermische machine is, maar haast je niet om het te kopen. Herinner je je wat we zeiden over de omkeerbaarheid van processen? Ze moeten heel, heel langzaam gebeuren, dus de uitgangskracht van deze machine is praktisch nul.

Menselijk metabolisme

Mensen hebben energie nodig om al hun systemen te laten werken, daarom gedragen ze zich als thermische machines die energie ontvangen en omzetten in mechanische energie om bijvoorbeeld te bewegen.

Efficiëntie En van het menselijk lichaam bij het doen van een werk kan worden gedefinieerd als de verhouding tussen het mechanische vermogen dat het kan bieden en de totale energie -ingang, die met voedsel hoort.

Zoals het gemiddelde vermogen P_M Het is W -werk gedaan in een tijdsinterval AT, Het kan worden uitgedrukt als:

P_M = W/Δt

Ja Δu/Δt Het is de snelheid waartoe energie wordt toegevoegd, de lichaamsefficiëntie blijft bestaan:

Er wordt aangenomen dat efficiëntie een positieve hoeveelheid is, wat wordt gewaarborgd door middel van absolute waardestaven in de vorige formule.

Door middel van talloze tests met vrijwilligers zijn de efficiëntie van maximaal 17%verkregen, wat gedurende meerdere uren ongeveer 100 watt vermogen levert.

Dit zal natuurlijk grotendeels afhangen van de taak die is gedaan. Een fiets trappen heeft een beetje grotere efficiëntie, van ongeveer 19 %, terwijl repetitieve taken met messen, pieken en schoffels een efficiëntie hebben van ongeveer 3 %.

Voorbeelden

De tweede wet van de thermodynamica is impliciet in alle processen die zich voordoen in het universum. Entropie groeit altijd, hoewel het in sommige systemen lijkt af te nemen. Om dit elders te zijn toegenomen, zodat het in het totale saldo positief is.

- Bij het leren is er entropie. Er zijn mensen die dingen goed en snel leren, naast het gemakkelijk kunnen onthouden. Er wordt gezegd dat ze mensen zijn met een laag leren van entropie, maar ze zijn zeker minder talrijk dan die van hoge entropie: degenen die het meest hebben onthouden de dingen die ze bestuderen.

- Een bedrijf met ongeorganiseerde werknemers heeft meer entropie dan een bedrijf waarin werknemers op een ordelijke manier taken uitvoeren. Het is duidelijk dat deze laatste efficiënter zal zijn dan de eerste.

- Wrijvingskrachten genereren minder efficiëntie bij het functioneren van machines, omdat ze de hoeveelheid gedissipeerde energie verhogen die niet efficiënt kan worden gebruikt.

- Het lanceren van een dobbelstenen heeft een grotere entropie dan een munt in de lucht gooien. Het lanceren van een valuta heeft immers slechts 2 mogelijke resultaten, terwijl het lanceren van de dobbelstenen 6 is. Hoe meer gebeurtenissen waarschijnlijk zijn, hoe meer entropie bestaat.

Kan u van dienst zijn: wat zijn de elementen van de beweging?

Opgeloste oefeningen

Oefening 1

Een cilinder met een zuiger is gevuld met een mengsel van vloeistof en waterdamp bij 300 K en 750 kJ warmte wordt overgebracht naar een constant drukproces. Als gevolg hiervan wordt de vloeistof in de cilinder verdampt. Bereken de verandering van entropie in het proces.

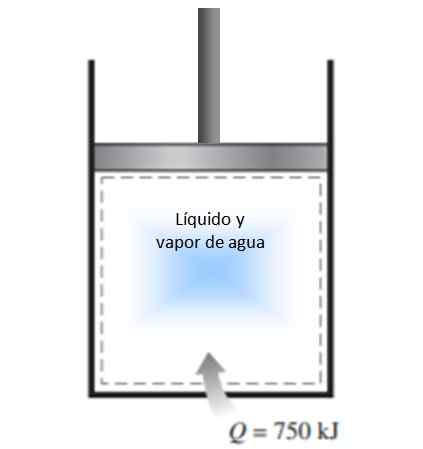Figuur 4. Figuur voor het voorbeeld opgelost 1. Bron: f. Zapata.

Oplossing

Het in de verklaring beschreven proces wordt uitgevoerd bij constante druk in een gesloten systeem, dat geen massa -uitwisseling ervaart.

Omdat het verdamping is, waarin de temperatuur niet verandert (tijdens faseveranderingen is de temperatuur constant), kan de definitie van hierboven gegeven entropiewijziging worden toegepast en kan de temperatuur buiten de integraal achterlaten:

Evalueren met de verstrekte gegevens:

Δs = 750.000 J / 300 K = 2500 J / K.

Omdat het systeem naar het systeem komt, is de verandering in entropie positief.

Oefening 2

Een gas lijdt een drukverhoging van 2.00 tot 6.00 Atmosferen (ATM), met een constant volume van 1.00 m³, en vervolgens uitzetten bij constante druk tot het een volume van 3 bereikt.00 m³. Keer eindelijk terug naar zijn initiële status. Bereken hoeveel werk wordt uitgevoerd in 1 cyclus.

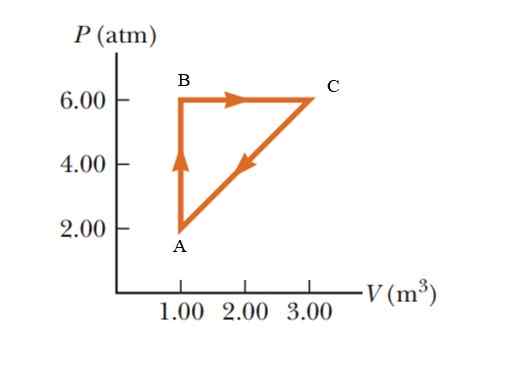Figuur 5. Thermodynamisch proces in een gas bijvoorbeeld 2. Bron: Serway -vulle. Fundamentals of Physics.

Oplossing

Het is een cyclisch proces waarbij de interne energievariatie nietig is, volgens de eerste wet van de thermodynamica, daarom q = w. In een p -v -diagram (druk - volume) is het werk dat tijdens een cyclisch proces is uitgevoerd, equivalent aan het gebied dat wordt vergrendeld door de curve. Om de resultaten in het internationale systeem te geven, is het noodzakelijk om eenheden te wijzigen in de druk door de volgende conversiefactor:

1 atm = 101.325 kPa = 101.325 PA.

Het door de grafiek omsloten gebied komt overeen met dat van een driehoek waarvan de basis (3 - 1 m³) = 2 m³ en wiens hoogte is (6 - 2 atm) = 4 atm = 405.300 PA

W_ABCA = ½ (2 m³ X 405300 PA) = 405300 J = 405.3 kJ.

Oefening 3

Er wordt gezegd dat een van de meest efficiënte machines die zijn gebouwd een stoomturbine is die wordt gevoed door steenkool op de Ohio -rivier, die wordt gebruikt om een ​​elektrische generator aan te drijven die werkt tussen 1870 en 430 ° C.

Bereken: a) Maximale theoretische efficiëntie, b) Het mechanische vermogen dat door de machine wordt afgeleverd indien geabsorbeerd 1.40 x 10⁵ J van energie elke seconde van de hete tank. Het is bekend dat echte efficiëntie 42 is.0%.

Oplossing

a) De maximale efficiëntie wordt berekend met de hierboven gegeven vergelijking:

Maximale efficiëntie = (q_Ingang - Q _Uitgang) /Q_Ingang = 1 - (T₂/T₁))

Om de Celsius door te geven aan Kelvin, is het voldoende om 273 toe te voegen.15 bij de Celsius -temperatuur:

Vermenigvuldiging met 100% heeft u een maximale percentage -efficiëntie, dat is 67.2%

c) Als de reële efficiëntie 42%is, is er een maximale efficiëntie van 0.42.

Het geleverde mechanische vermogen is: P = 0.42 x 1.40 x10 ⁵ J/s = 58800 W.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Cengel, en. 2012. Thermodynamica. 7^ma Editie. McGraw Hill.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 4. Vloeistoffen en thermodynamica. Uitgegeven door Douglas Figueroa (USB).
4. Ridder, r.  2017. Fysica voor wetenschappers en engineering: een strategiebenadering.
5. López, c. De eerste wet van de thermodynamica. Hersteld van: culturracientifica.com.
6. Serway, r. 2011. Fundamentals of Physics. 9^NA Cengage leren.
7. Sevilla University. Thermische machines. Hersteld van: laplace.ons.is