Tweede balansvoorwaarde Verklaring, voorbeelden, oefeningen

De Tweede evenwichtstoestand Het stelt vast dat de som van de knooppunten of momenten die worden geproduceerd door alle krachten die op een lichaam werken, ongeacht welk punt wordt berekend, moet worden geannuleerd, zodat deze lichaam in statisch of dynamisch evenwicht is.

Het koppel of het moment van kracht aangeven door de Griekse brief τ, Wiskundig wordt het als volgt uitgedrukt:

∑ τ = 0

Figuur 1. Om de rocker in evenwicht te brengen, is het noodzakelijk om de tweede evenwichtstoestand toe te passen. Bron: Pxhere.

De gewaagde letter geeft de vector aard van het moment aan, die moet worden geannuleerd ten opzichte van elk punt dat wordt gekozen als een spincentrum. Op deze manier is het annuleren van het netto koppel, het is gegarandeerd dat het object niet begint te draaien of draaien.

Als het object echter al eerder roteerde en het netto koppel plotseling verdwijnt, zal de rotatie doorgaan, maar met constante hoekige snelheid.

De tweede evenwichtstoestand wordt gebruikt in combinatie met de eerste voorwaarde, die zegt dat de som van de krachten op een lichaam nietig moet zijn, zodat deze niet beweegt, of dat als dit het geval is, het is met uniforme rechtlijnige beweging:

∑ F = 0

Beide voorwaarden zijn van toepassing op uitgebreide lichamen, die wier afmetingen meetbaar zijn. Wanneer een object een deeltje zou moeten zijn, heeft het geen zin om te praten over rotaties, en de eerste voorwaarde om te garanderen is voldoende.

Voorbeelden

De tweede evenwichtstoestand wordt in talloze situaties onthuld:

Bij het beklimmen van de trap

Bij het ondersteunen van een trap op de vloer en de muur hebben we genoeg nodig om te wrijven, vooral op de vloer, om ervoor te zorgen dat de trap niet glijdt. Als we proberen te klimmen op een ladder die wordt ondersteund op een olieachtige, natte of gladde vloer, is het niet moeilijk om te anticiperen dat we zullen vallen.

Om de trap vol vertrouwen te kunnen gebruiken, is het noodzakelijk dat deze in statisch evenwicht is tijdens het klimmen en wanneer deze in de stap is die nodig is.

Het kan je van dienst zijn: Pluto (Dwarf Planet)

Een kast verplaatsen

Wanneer u een hoog meubilair als een kast wilt verplaatsen, of een stuk waarvan het high groter is dan het breed is, is het handig om op een dieptepunt te duwen, om te voorkomen dat u vernietigt, op deze manier is het waarschijnlijker dat het meubilair in plaats daarvan zal glijden van draaien en liggen.

In dergelijke omstandigheden is het meubilair niet noodzakelijkerwijs in evenwicht, omdat het snel kan worden verplaatst, maar het zou tenminste niet draaien.

Balkons

De balkons die uitblinken dat de gebouwen moeten worden gebouwd, garanderen dat, hoewel er veel mensen bovenaan zijn, het niet draait en instort.

Diëlektrisch in externe elektrische velden

Bij het plaatsen van een diëlektrisch materiaal in een extern elektrisch veld bewegen en roteren de moleculen om een ​​evenwichtspositie aan te nemen, waardoor een elektrisch veld in het materiaal ontstaat.

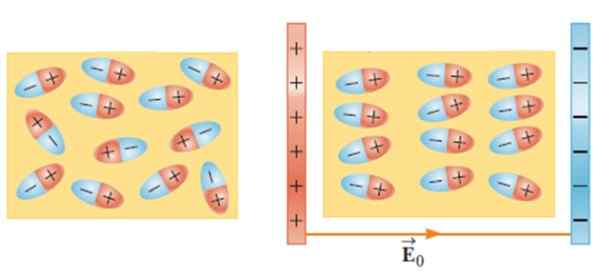Figuur 2.- Zonder extern elektrisch veld zijn de dipolen gerandomiseerd (links). Het externe veld past een koppel toe op diëlektrische moleculen en deze zijn gereorganiseerd. Bron: Serway, r. Natuurkunde voor wetenschap en engineering.

Dit effect zorgt ervoor dat de capaciteit van een condensor toeneemt wanneer een materiaal zoals glas, rubber, papier of olie tussen zijn pantser wordt geïntroduceerd.

Borden en lampen

Het is gebruikelijk dat veel gebouwen kennisgevingen op de bouwmuur ophangen, zodat ze zichtbaar zijn voor voorbijgangers.

De poster wordt vastgemaakt door een balk en een kabel, beide op de muur gefixeerd met behulp van steunen. De verschillende krachten die handelen moeten ervoor zorgen dat de poster niet valt, waarvoor de twee evenwichtsvoorwaarden in actie komen.

Een reflector in een park kan ook op deze manier worden geplaatst, zoals in de volgende figuur:

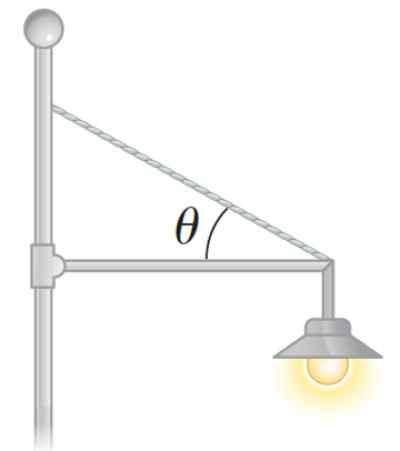figuur 3. Een statische balanslamp. Bron: Serway. Natuurkunde voor wetenschap en engineering.

Hoe het netto koppel of het netto moment van een kracht te berekenen?

Het koppel of moment van kracht, aangeduid door τ of M In sommige teksten wordt het altijd berekend met betrekking tot een punt waar de rotatieas passeert.

Het wordt gedefinieerd als het vectorproduct tussen de positievector R, dat is gericht van de as tot het punt van toepassing van kracht en kracht F:

Kan u van dienst zijn: thermodynamisch evenwicht: klassen en toepassingen

τ = R × F

Als een vector is het noodzakelijk om het koppel uit te drukken dat zijn grootte, richting en betekenis geeft. De omvang wordt gegeven door:

τ = rf.Sin θ

Juiste regel voor het vectorproduct

Wanneer het probleem zich in het vlak bevindt, staat het koppeladres loodrecht op het papier of het scherm en wordt de richting bepaald door de rechterhandregel, waarin de index naar R, De middelvinger naar F en de duim signalen in of uit papier.

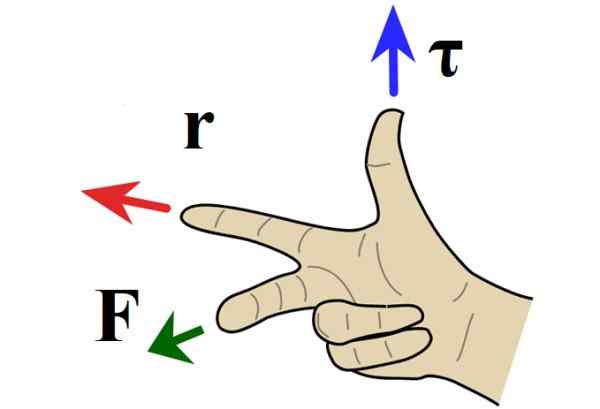Figuur 4. Rechtsregel voor vectorproduct. Bron: Wikimedia Commons.

Wanneer het koppel uit het papier wijst, bevindt de rotatie zich in de tegenovergestelde richting van de kloknaalden en krijgt u een positief teken toegewezen door de conventie. Als in plaats daarvan het koppel in het vel wordt gericht, is de rotatie in de richting van de handen en een negatief teken.

Om het netto koppel te vinden, wordt een handig punt voor de berekening gekozen, die kan zijn dat de grootste hoeveelheid krachten handelt. In dit geval is het moment van deze krachten nietig, voor het hebben van een positievector R van grootte 0.

U kunt elk punt kiezen dat voldoende informatie biedt om het onbekende te wissen dat vraagt ​​om het probleem op te lossen. Laten we het dan in meer detail bekijken.

Oefening opgelost

De reflector van de volgende figuur heeft 20 kg massa en wordt ondersteund door een horizontale dunne balk, van verachtelijke massa en lengte L, die is gearticuleerd in een paal. De kabel, ook licht, die helpt de reflector te ondersteunen, vormt een hoek θ = 30 º met de balk. Berekenen:

a) De spanning in de kabel

b) De grootte van de kracht f die de paal uitoefent op de balk door het scharnier.

Oplossing

We zullen de eerste evenwichtstoestand ∑ toepassen F = 0 naar de krachten die in het diagram worden getoond:

Kan u van dienst zijn: geabsorbeerde hitte: formules, hoe u het kunt berekenen en oefeningen opgelost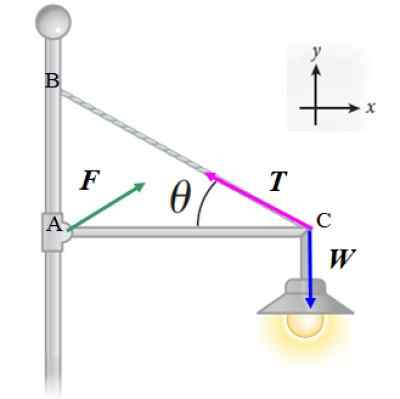

F + T + W = 0

Merk op dat de omvang en richting van F Ze moeten nog worden bepaald, maar we gaan ervan uit dat het twee componenten heeft: F_X en f_En. Op deze manier krijgen we twee vergelijkingen:

F_X -T. cos θ = 0

F_En - W + t⋅ sin θ = 0

Laten we nu de tweede evenwichtstoestand toepassen en punt A kiezen, omdat we de omvang van niet weten F noch die van T. Bij het kiezen van dit punt, de vector R_NAAR is nietig, daarom het moment van F is nietig en de omvang van F Het zal niet in de vergelijking verschijnen:

-W⋅l + t⋅sen θ⋅l = 0

Daarom:

T.Sin θ.L = W.L

T = w/sen θ = (20 kg x 9.8 m/s²) / Sin 30 º = 392 n

Als we de grootte van T kennen, kunnen we de component fruimen f_X:

F_X = T⋅ cos θ = 392 cos 30º n = 339. 5 n

En vervolgens component f_En:

F_En = W - t⋅ sin θ = (20 kg x 9.8 m/s²) - 392⋅sen 30 º = 0

Dan kunnen we uitdrukken F Dus:

F = 339.5 n X

Het is daarom een ​​horizontale kracht. Dit komt omdat we bedenken dat de bar verachtelijk gewicht had.

Als punt C was gekozen om het resulterende moment te berekenen, de vectoren R_T En R_W Ze zijn daarom nietig:

M = F_Y⋅L = 0

Er wordt geconcludeerd dat f_En = 0. Dus:

- W + t⋅ sin θ = 0

T = w/ sin θ

Dat is hetzelfde resultaat dat aanvankelijk wordt verkregen door punt A te kiezen als de plaats waar de rotatieas passeert.

Thema's van belangstelling

Evenwichtsvoorwaarden.

Eerste balansvoorwaarde.

Referenties

1. Bedford, 2000. NAAR. Mechanica voor engineering: statisch. Addison Wesley.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 4. Deeltjessystemen. Uitgegeven door Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.
5. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.