Conische secties typen, toepassingen, voorbeelden

De conische secties Ze zijn de curven die worden verkregen door een vlak met een kegel te onderscheppen. Er zijn verschillende manieren om dit te doen; Als het vlak bijvoorbeeld loodrecht op de axiale as van de kegel wordt geleid, wordt een omtrek verkregen.

Het vlak een beetje kantelen ten opzichte van de axiale as van de kegel wordt een ellips verkregen, een curve die is gesloten, maar als we het nog meer neigen een parabool of een hyperbool wordt verkregen, zoals te zien is in de animatie 1.

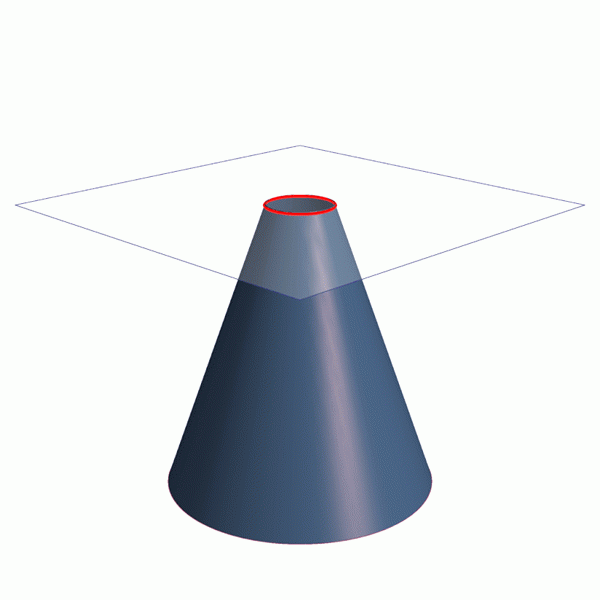Animatie die laat zien hoe de vier conische secties te verkrijgen: omtrek, gelijkenis en hyperbool ellips. Bron: Wikimedia Commons. Lijnen / CC0

De conische secties maken deel uit van de natuur en de wereld om ons heen. Engineering, architectuur en astronomie zijn belangrijke takken van kennis die gebruik maken van conica.

[TOC]

Voorwaarden voor conische secties

De conische secties worden gedefinieerd als geometrische plaatsen die voldoen aan de volgende voorwaarden:

Gelijkenis

Het is de geometrische plaats van alle punten die in een gelijklijk vlak liggen naar een vast punt dat wordt genoemd focus F en een rechte lijn ook vast, genoemd, genoemd richtlijn.

Ovaal

Een vliegtuigpunt behoort tot een ellips als de som van de afstanden tussen dat punt en twee andere vaste punten, genaamd Focus en gelegen op de grote as van de ellips blijft constant.

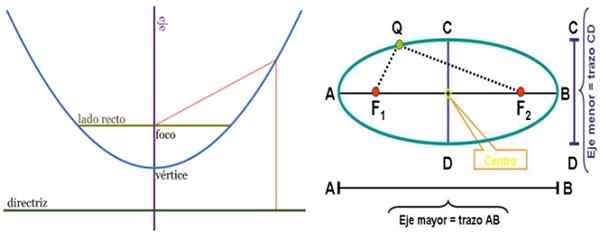De gelijkenis links en de ellips rechts, met hun respectieve elementen. De foci zijn punten met veel toepassingen. Bron: Wikimedia Commons.

Omtrek

Het is de geometrische plaats van alle punten die dezelfde afstand behouden tot een ander punt genaamd Centro. Deze afstand is de radio van de omtrek.

Kan u van dienst zijn: Euclidian Afstand: concept, formule, berekening, voorbeeld

Hyperbool

Set punten in het vlak zodanig dat het verschil tussen de afstand tot twee vaste punten wordt genoemd Focus, het is constant.

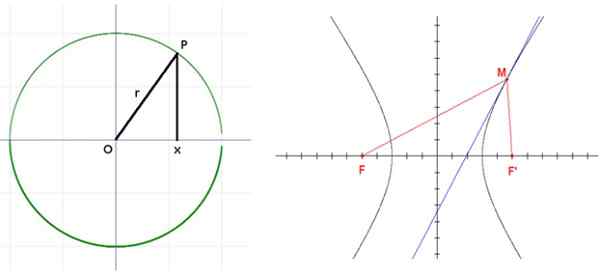Hyperbool met foci f en f. Bron: Wikimedia Commons.

Toepassingen

Laten we eens kijken naar enkele van de conische secties -toepassingen:

Gelijkenissen  

-Wanneer een object wordt gelanceerd, heeft het traject dat volgt een parable vorm.

-De gelijkenissen hebben opmerkelijke engineeringtoepassingen, bijvoorbeeld in de gesuspendeerde bruggen schieten de kabels op in de vorm van gelijkenissen.

-De gelijkenissen zijn ook goed om reflectoren en telescopen te maken. Dit is te danken aan een interessante eigenschap: bij het plaatsen van een armatuur in de focus van een parabolisch dwarsdoorsnedeoppervlak, zal het licht in parallelle stralen naar de gelijkenisas reizen.

-Als de lichtstralen parallel aan de symmetrieas naderen, concentreert het hen in de focus, een omstandigheid die wordt gebruikt om reflector -telescopen te maken, zoals de Hale de Monte Palomar -telescoop.

Ellipsen

-De planeten van het zonnestelsel bewegen na elliptische trajecten, vrij dicht bij de omtrek in het geval van de grote planeten, het land inbegrepen. De zon staat niet in het midden, maar in een van de schijnwerpers.

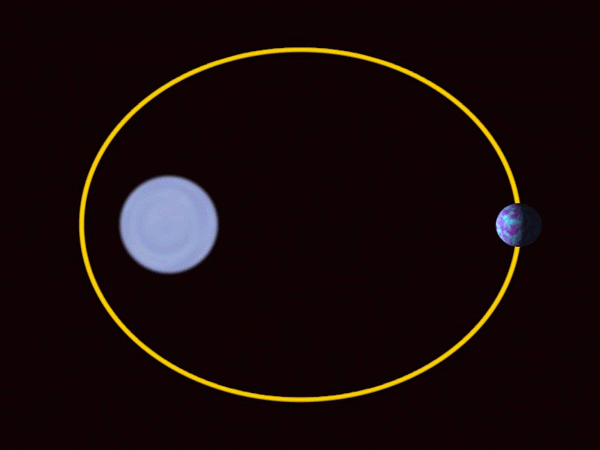De planeten van het zonnestelsel bewegen in elliptische banen met de zon in een van de schijnwerpers. Bron: Wikimedia Commons.

-De ellips wordt veel gebruikt in de architectuur als een decoratief en ontwerpelement.

-Door een reflector in een van de schijnwerpers van een ellips te plaatsen, wordt het licht gereflecteerd in de richting van de andere focus. Hetzelfde gebeurt met geluid. Dat is de reden waarom in ellips -vormige zalen, die rustig in de ene focus spreken, duidelijk worden gehoord door luisteraars in de andere focus.

Het kan je van dienst zijn: hepagonaal prisma

-Deze zelfde eigenschap heeft een verrassende toepassing op het gebied van geneeskunde. Nierberekeningen kunnen worden vernietigd door geluid. Echografie golven van grote intensiteit worden gegenereerd in een van de foci van een elliptisch bad vol water, en de patiënt bevindt zich in de andere focus. Geluidsgolven beïnvloeden en reflecteren in de berekening, en met hun energie fragmenteren ze het in kleine stukjes, die de persoon vervolgens gemakkelijk uitsteekt tijdens het urineren.

Hyperbolen

-Sommige kometen in het zonnestelsel volgen hyperbolische trajecten, altijd met de zon in een van de foci.

-Hyperbolen focussen zijn ook erg interessant om de fenomenen van golfreflectie te bestuderen. Door bijvoorbeeld een lichtstraal naar de focus van een parabolische spiegel te richten, wordt dit weerspiegeld in de andere focus, een zeer nuttige eigenschap voor het bouwen van telescopen, omdat het licht kan focussen op een parabolische spiegel en wordt omgeleid naar een andere meer geschikte plaats Volgens ontwerp.

-De koeltorens van nucleaire planten hebben hyperbolenvormig silhouet.

-Vóór de komst van GPS werden hyperbolen gebruikt in navigatie om boten te vinden. De schepen die aan boord werden gedragen signalen die gelijktijdig werden uitgegeven door de radio A- en B -stations en een computer was verantwoordelijk voor het registreren van de verschillen van de aankomsttijden van de signalen, om ze te transformeren in verschillen van afstanden van afstanden. Op deze manier bevindt het schip zich in de tak van een hyperbool.

De procedure wordt herhaald met twee andere radio C- en D -stations, die het schip in de tak van plaatst Nog een hyperbool. De definitieve positie van de boot is de kruising van beide hyperbolen.

Kan u van dienst zijn: GROTE FUNCTIE: Hoe u het kunt identificeren, voorbeelden, oefeningen

Omtrek

-De komst van het wiel veranderde de loop van de geschiedenis.

-De cirkelvormige beweging is heel gebruikelijk, veel stukken draaien om verschillende effecten te produceren, van molens tot fans.

-Hoewel de trajecten van de belangrijkste planeten elliptisch zijn, zijn de cirkelvormige trajecten in veel gevallen goede benaderingen.

-Circunferenties zijn frequente elementen in architectuur, ontwerp, engineering en constructie. De lijst met cirkelvormige of schijfvormen is eindeloos: munten, cd's, horloges en meer.

Voorbeelden

Dan zijn er twee conics in het vliegtuig, een cirkel en een ellips.

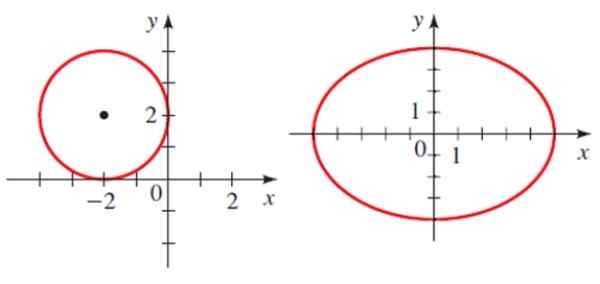Voorbeelden van conische secties: een cirkel en een ellips. Bron: Stewart, J. Voorzetting.

Elk heeft een analytische vergelijking:

Omtrek

(X-H)² + (Y-K)² = R²

Waarbij h en k de coördinaten van het centrum zijn en r de radio is. Voor de omtrek in de figuur is de vergelijking:

(x+2)² + (Y-2)² = 4

Ovaal

De ellipsvergelijking waarvan het centrum het coördinaatpunt is (H, K):

[(X-H)² /naar² ]+ [(y-k)² /B² ] = 1

Waar a en b de semi -piles van de ellips zijn. Voor de getoonde ellips bevindt het centrum zich op punt 0.0, het grootste semi -hetzelfde is hetzelfde en de kleine semije is 4. Daarom is de vergelijking ervan:

(X² /25)+ (en² / 16) = 1

Referenties

1. Hoffman, J. Selectie van wiskundeproblemen. Deel 2.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
4. Wikipedia. Kegelgedeelte. Hersteld van: is.Wikipedia.borg.
5. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.