Simpson Rule -formule, demonstratie, voorbeelden, oefeningen

De Simpson -regel Het is een methode om ongeveer gedefinieerde integralen te berekenen. Het is gebaseerd op het verdelen van het integratie-interval in een paar subintervalo's gelijkmatig verdeeld.

De extreme waarden van twee opeenvolgende sub-interval definiëren drie punten, die een parabool aanpassen, waarvan de vergelijking een tweedegraads polynoom is. 

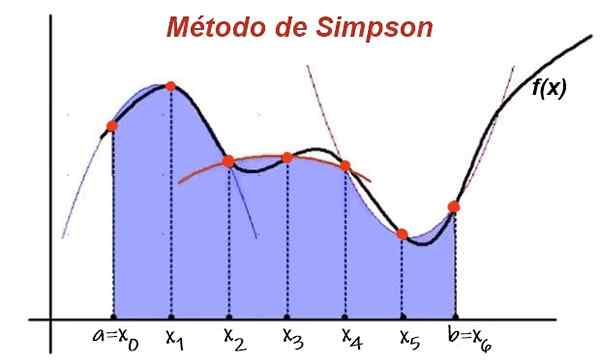
Figuur 1. In de Simpson -methode wordt het integratie -interval onderverdeeld in een paar intervallen van gelijke breedte. De functie wordt benaderd door een gelijkenis in elke 2 sub-intervalos en de integrale benaderingen door de som van het gebied onder de gelijkenissen. Bron: UPV.is.

Vervolgens wordt het gebied onder de curve van de functie in de twee opeenvolgende intervallen geschat door het interpolatiepolynoomgebied. Door de bijdrage toe te voegen aan het gebied onder de gelijkenis van alle opeenvolgende sub-intervallen, is er de geschatte waarde van de integraal.

Aan de andere kant, aangezien de integrale van een gelijkenis kan worden berekend, is het mogelijk om een ​​analytische formule te vinden voor de geschatte waarde van de gedefinieerde integrale. Staat bekend als de Simpson -formule.

De fout van het aldus verkregen resultaat neemt af in de mate dat het aantal onderverdelingen n groter is (is N A Koppel).

Hieronder zal een uitdrukking worden gegeven die het bovenste niveau van de naderingsfout voor de integrale I mogelijk maakt, wanneer een partitie van reguliere subintervallen van het totale interval [a, b] is gemaakt [b].

[TOC]

Formule

Het integratie -interval [a, b] is onderverdeeld in n subintervallen waarbij N een koppel is. De breedte van elke onderverdeling zal zijn:

H = (b - a)/n

Op deze manier wordt op het interval [a, b] de partitie gemaakt:

X0, x1, x2, ..., xn-1, xn

Zijn x0 = a, x1 = x0 + h, x2 = x0 + 2h,…, xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Het kan u van dienst zijn: verschil tussen cirkel en omtrek (met voorbeelden)

De formule die het mogelijk maakt om de gedefinieerde integrale en continue functie te berekenen, en bij voorkeur zacht, in het interval [a, b] is:

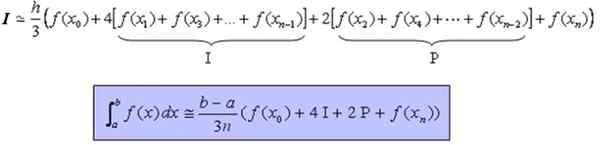
Demonstratie

To obtain the Simpson formula, in each subinterval [XI, XI+2] the function f (x) approaches by a second degree P (x) polynomial (parable) that passes through the three points: [xi, f (f (f (F (F (F (F (F (F (F (F (F (F (F (F XI)]; [Xi+1, f (xi+1)] en [xi+2, f (xi+2)]]].

Vervolgens wordt de integrale polynoom p (x) berekend in [xi, xi+2] die de integrale van functie f (x) in dat interval benadert.

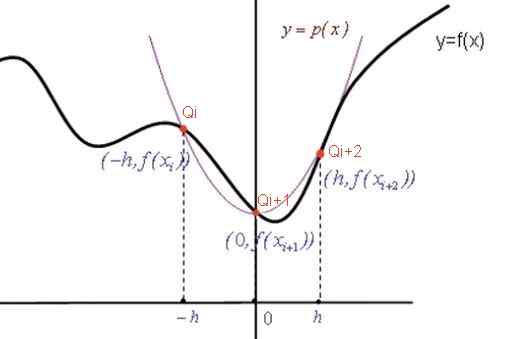Figuur 2. Grafiek om de Simpson -formule te demonstreren. Bron: f. Zapata.

Interpolatie polynoomcoëfficiënten

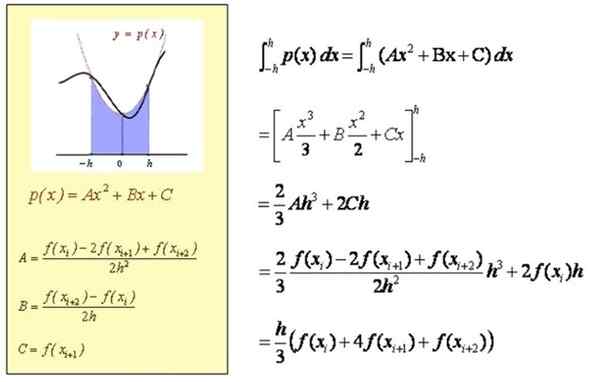
De paraboolvergelijking P (x) heeft de algemene vorm: p (x) = a x² + B X + C. Naarmate de gelijkenis door de punten gaat die in rood worden aangegeven (zie figuur), worden de coëfficiënten A, B, C bepaald uit het volgende systeemsysteem:

AH)² - B H + C = F (xi)

C = F (xi+1)

AH)² + B H + C = F (xi + 2)

Opgemerkt kan worden dat coëfficiënt C wordt bepaald. Om de coëfficiënt te bepalen, voegen we de eerste en derde vergelijking toe:

2 a h² + 2 c = f (xi) + f (xi + 2).

Dan wordt de waarde van C vervangen en het is duidelijk:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²))

Om de coëfficiënt B te bepalen, wordt de derde vergelijking van de eerste afgetrokken en B verwijderd van zichzelf:

B = [f (xi+2) - f (xi)] = 2 h.

Samenvattend heeft de tweede graad polynoom p (x) die door de punten qi, qi+1 en qi+2 gaat, coëfficiënten:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²))

B = [f (xi+2) - f (xi)] = 2 h

C = F (xi+1)

Berekening van de geschatte integrale in [xi, xi+2]

Geschatte berekening van de integraal in [A, B]

Zoals al is gezegd, op het totale integratie -interval [a, b] een partitie x0, x1, x2, ..., xn -1, xn met stap h = xi+1 - xi = (b - (b -) / n, waar n een stel is.

Kan u van dienst zijn: bemonsteringsfout: formules en vergelijkingen, berekening, voorbeelden

Vervolgens is de integraal gedefinieerd in het totale interval [a, b] de som van de integralen in de subintervals [xi, xi+2], die worden benaderd door de integralen van de interpolatie polynomen p (x):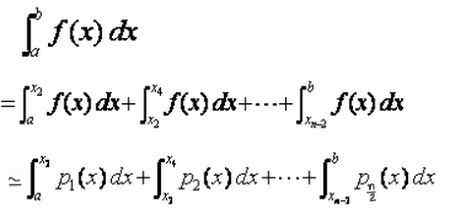

In de vorige sectie werd de formule voor polynoomintegralen in de subintervallen gevonden. Dit resultaat toepassen op elke integraal heeft: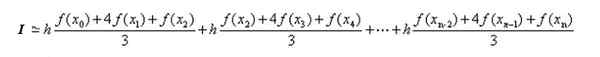

Die als volgt op een meer compacte manier kan worden herschreven: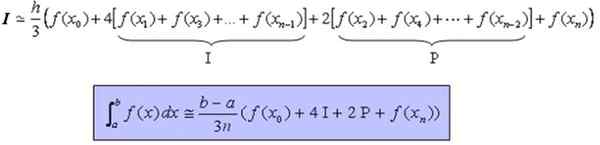

Benaderfout

Als de functie waarnaar u in het interval wilt integreren [A, B] tot de vierde orde, continu in dat interval heeft afgeleid, is het mogelijk om een ​​formule te vinden die het maximale foutniveau in de aanpak kan bepalen door middel van middelen van de Simpson SN -formule Voor de waarde van de integraal: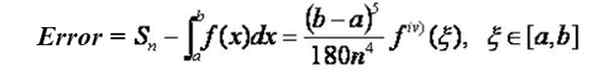

Merk op dat de fout afneemt met het vierde vermogen van het interval -onderverdelingennummer. Als u bijvoorbeeld van N -onderverdelingen naar 2n gaat, neemt de fout af met een 1/16 factor.

Het bovenste foutniveau verkregen door de Simpson -benadering kan worden verkregen uit dezelfde formule, ter vervanging van het vierde derivaat door de maximale absolute waarde van het vierde derivaat in het interval [a, b].

Opgeloste voorbeelden

- voorbeeld 1

Overweeg de functie f (x) = 1 / (1 + x²)). 

Zoek de gedefinieerde integrale van de F (x) -functie in het interval [-1, 1] met behulp van de Simpson-methode met twee onderverdelingen (n = 2).

Oplossing 

Wordt genomen n = 2. De integratielimieten zijn a = -1 en b = -2, dan is de partitie als volgt: 

X0 = -1; X1 = 0 en x2 = +1.

Daarom gaat de formule van Simpson als volgt aan:

Met n = 2 → xo = -1, x1 = 0; x2 = 1, daarom:

- Voorbeeld 2

Overweeg de functie f (x) = 1 / (1 + x²)). 

Zoek de gedefinieerde integrale van de functie f (x) in het interval [-1, 1] door de Simpson-formule met vier onderverdelingen (n = 4).

Het kan u van dienst zijn: schatting per intervallen

Oplossing 

Wordt genomen n = 4. De integratielimieten zijn a = -1 en b = -2, dan is de partitie als volgt: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 en x4 = +1.

De formule van Simpson is als volgt vastgesteld:

Integraal ≃ [(b -a)/(3 n)] [f (x0) + 4 i + 2 p + f (xn)]

Voor het geval waarin het wordt toegepast, is het als volgt:

Integraal ≃ (1- (1))/(3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)

Integraal ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1.5666

- Voorbeeld 3

Bepaal de gedefinieerde integrale van de vorige voorbeelden exact en maak een vergelijking van het exacte resultaat met die verkregen door de Simpson -formule in voorbeelden 1A en 1B.

Oplossing 

De onbepaalde integrale van de functie f (x) = 1 / (1 + x²) is de functie Arctan (x).

Bij het evalueren van de integratielimieten:

Integraal = arctan (1) - arctan (-1) = π/4 - (-π/4) = π/2 = 1.5708

Als we het resultaat van de exacte oplossing vergelijken met die verkregen door de Simpson -methode met n = 2 en n = 4 hebben we:

Voor n = 2 is het verschil tussen de exacte en de geschatte oplossing π/2 -5/3 = -0959, dat wil zeggen een percentage verschil van -0,06%.

En voor de Simpson -aanpak met n = 4 is het verschil tussen de exacte en de geschatte oplossing π/2 - 47/30 = 0,0041, dat wil zeggen een percentage verschil van 0,003%.

Voorgestelde oefening

De methode van Simpson is geschikt om te worden toegepast in programmeertalen en computertoepassingen gericht op wiskundige berekeningen. Het wordt voorgesteld aan de lezer die, op basis van de formules die in dit artikel worden gegeven, zijn eigen code schrijven in zijn favoriete programma.

De volgende figuur toont een oefening waarin de Simpson -formule is geïmplementeerd in Smath Studio, Gratis software beschikbaar voor besturingssystemen ramen En Android.

figuur 3. Voorbeeld van numerieke integratie via de Simpson -regel met behulp van software. Bron: f. Zapata.

Referenties

1. Casteleiro, J. M. 2002. Uitgebreide berekening (geïllustreerde editie). Madrid: ESIC -redactie.
2. UPV. Simpson -methode. Polytechnic University of Valencia. Hersteld van: YouTube.com
3. Purcell, E. 2007. Negende editie berekening. Prentice Hall.
4. Wikipedia. Simpson -regel. Hersteld van: is.Wikipedia.com
5. Wikipedia. Lagrange polynoom interpolatie. Hersteld van: is.Wikipedia.com