Wat zijn driehoekige cijfers? Eigenschappen en demonstraties

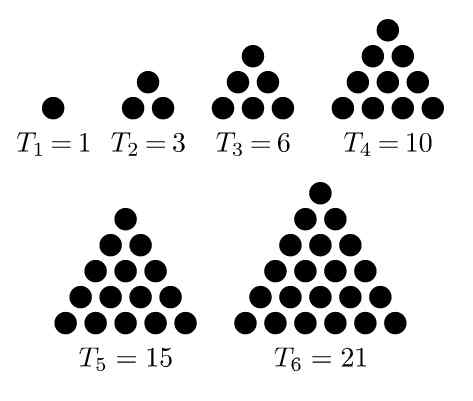
Het is bekend als driehoekige nummers naar de volgorde van getallen die worden verkregen door een opstelling of figuur van punten van een gelijkzijdige driehoek te maken. De eerste van de reeks is: 1, 3, 6, 10, 15, 21, ..

Het eerste driehoekige probleem is 1, de tweede is de 3, omdat het wordt verkregen door het toevoegen van een rij met twee punten aan de vorige, om een ​​gelijkzijdige driehoek van drie elementen te vormen.

Figuur 1. Volgorde van de eerste zes driehoekige nummers. Bron: Wikimedia Commons. Melchoir/cc by-sa (https: // creativeCommons.Org/licenties/by-sa/3.0)

De derde is 6, wat verschijnt bij het toevoegen van een rij met drie punten aan de vorige opstelling, zodat een driehoek met drie punten per zijde wordt gevormd. De 10 van de volgorde wordt verkregen door een andere rij toe te voegen aan de vorige opstelling, zodat een driehoek met vier punten per zijde wordt gevormd.

De formule waarmee u het element kunt vinden N Uit de driehoekige volgorde is bekend dat het voorste driehoekige nummer is:

T_N = T_N-1 + N

De lijst met de eerste zes driehoekige nummers wordt als volgt bereikt:

-Eerst: 1

-Seconde: 1 + 2 = 3

-Derde: (1 +2) + 3 = 3 + 3 = 6

-Kamer: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Vijfde: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Zesde: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Eigenschappen van driehoekige getallen

1.- Het n-simo TN driehoekige aantal van de sequentie van driehoekige getallen is de helft van n vermenigvuldigd met n+1:

T_N = ½ n (n+1)

2.- De som van het driehoekige nummer n-Ésimo met het voorste driehoekige nummer, dat wil zeggen (n-1) -sheimo, het is vierkant verhoogd:

T_N + T_N-1= n²

3.- Het verschil in het driehoekige nummer n-dit minder de driehoekige n-Ésimo minder één is n:

T_N - T_N-1 = n

4.- De som van de eerste driehoekige getallen wordt het tetraëdrische nummer SN genoemd en is gelijk aan het zesde deel van het product vermenigvuldigd met (n + 1) en vermenigvuldigd met (n + 2):

Kan u van dienst zijn: belastend

S_N= ⅙ n (n + 1) (n + 2)

5.- Elk natuurlijk getal n is het resultaat van de som van drie driehoekige getallen:

N = Δ1 + Δ1 + Δ3

Deze laatste woning of stelling werd ontdekt door de grote wiskundige Carl Friedrich Gauss in 1796, die hij in zijn dagboek scoorde door de Griekse bewondering te plaatsen Eureka! wat betekent het "Ik heb het bereikt".

Dat was hetzelfde woord dat veel eerder werd gebruikt door de Griekse Archimedes toen hij het schijnbare gewicht van een ondergedompeld lichaam bepaalde.

In deze relatie wordt nul nummer als driehoekig beschouwd en kan er herhaling zijn.

Demonstraties

- Demonstratie 1

Bewijs dat het driehoekige nummer N-Dit is:

T_N = ½ n (n+1)

Het is gemakkelijk om de vorige formule af te leiden, als we ons realiseren dat we hetzelfde aantal punten kunnen toevoegen aan de driehoekige opstelling om een ​​vierhoek van punten te vormen.

Aangezien het totale aantal opstellingspunten in de vorm van een vierhoek het aantal rijen is N vermenigvuldigd met het aantal kolommen (N+1), Dan zal de driehoekige opstelling slechts de helft van de punten van de opstelling hebben in de vorm van een vierhoek.

Hier wordt geïllustreerd in figuur 2.

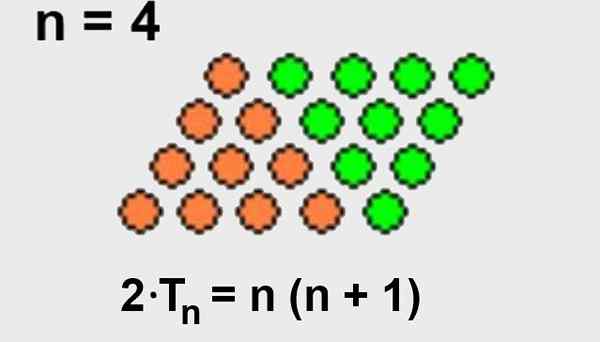Figuur 2. Vierkante -vormige opstelling waarin het totale aantal punten het aantal rijen is, is vermenigvuldigd met het aantal kolommen n+1. Het totale aantal punten is ook twee keer dat van de driehoekige opstelling. Bron: Wikimedia Commons.

- Demonstratie 2

Toon aan dat de som van N-Dit driehoekige nummer met de N-Hoe minder een driehoekig nummer is N Squared:

T_N + T_N-1= n²

Er is al aangetoond dat het driehoekige nummer N-Dit wordt gegeven door:

T_N= ½ n (n+1)

Daarom is het voorste driehoekige nummer:

T_N-1 = ½ (n-1) ((n-1) + 1) = ½ n (n-1)

De som van beide overblijfselen:

T_N + T_N-1 = ½ n (n + 1) + ½ n (n - 1)

½ n wordt genomen om te verkrijgen:

T_N + T_N-1 = ½ n [(n + 1) + (n - 1) = ½ n [n + 1 + n - 1]

En onmiddellijk wordt de uitdrukking vereenvoudigd in de beugel:

Het kan u van dienst zijn: schatting per intervallen

T_N + T_N-1 = ½ N [2 n] = ½ 2 n ⋅ n

Nu, herinneren dat ½ voor 2 1 is en dat n voor n n vierkant is, heb je:

T_N + T_N-1 = n²

Deze eigenschap kan ook geometrisch worden aangetoond, de driehoek is eenvoudig voltooid om een ​​vierkant te vormen, zoals weergegeven in figuur 3.

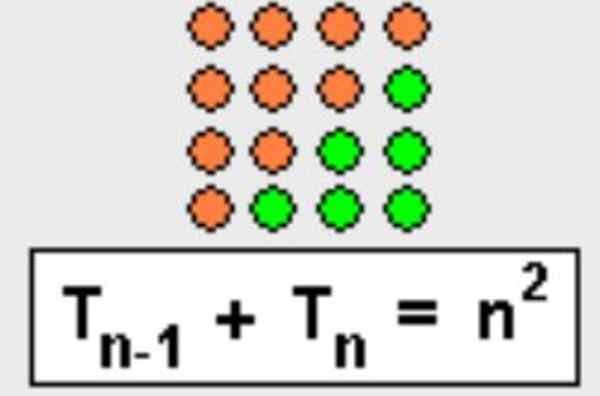figuur 3. De som van het driehoekige N-Ésimo-getal met het voorste driehoekige nummer is gelijk aan n vierkant. Bron: Wikimedia Commons.

- Demonstratie 3

Het verschil in het driehoekige aantal orde N minus het driehoekige aantal orde N-1 is n:

T_N - T_N-1 = n

Dit kan eenvoudig worden getest door te onthouden dat het volgende driehoekige nummer wordt verkregen van de vorige via de formule:

T_N = T_N-1 + N

En van daaruit is het duidelijk dat T_N - T_N-1 = n. Het is ook eenvoudig om het grafisch te visualiseren, zoals weergegeven in figuur 4.

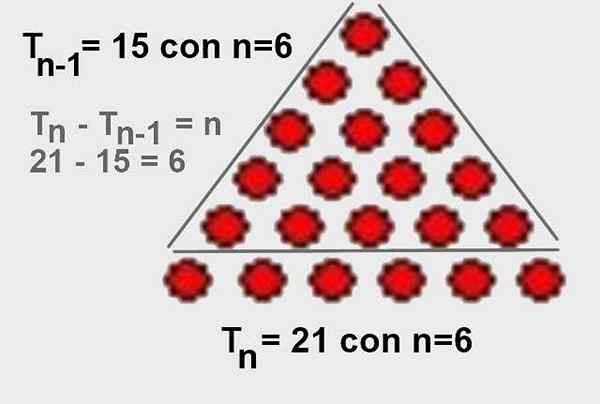Figuur 4. Het verschil van het driehoekige aantal orde n minder de voorste driehoek van orde n-1 is n. Bron: Wikimedia Commons.

- Demonstratie 5

De som van de eerste driehoekige n nummers sN Het is gelijk aan het zesde deel van het product vermenigvuldigd met (n + 1) en vermenigvuldigd met (n + 2):

S_N = ⅙ n (n + 1) (n + 2)

Laten we het driehoekige aantal orde n: T_N= ½ n (n+1). De som van de eerste N Driehoekige nummers zullen het voor S_N  

Bijvoorbeeld, S₁ betekent de som van de eerste driehoekige kwestie, die ongetwijfeld 1 zal zijn.

Laten we eens kijken of de formule die we proberen te proberen, wordt nageleefd met n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Inderdaad, de formule voor n = 1 is gecontroleerd. Het is gemakkelijk om te visualiseren dat de som van N+1 eerste driehoekige getallen de som zal zijn van de eerste n meer het volgende driehoekige nummer:

S_N+1 = S_N + T_N+1

Stel nu de formule van S_N Het is vervuld voor n, dan vervangen we het in de vorige uitdrukking en voegen het driehoekige aantal orde toe N+1:

S_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]

Kan u van dienst zijn: loodrechte lijn: kenmerken, voorbeelden, oefeningen

Laten we stap voor stap eens kijken wat is verkregen:

-We voeren de som van de twee fractionele uitdrukkingen uit:

S_N+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Het wordt verwijderd uit de gemeenschappelijke teller tot 2 (n + 1) (n + 2) en vereenvoudigt:

S_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Het vorige resultaat komt overeen met de S -formuleN Als n+1 wordt vervangen, die door inductie is aangetoond, de formule van de som van de eerste driehoekige termen.

Tetraëder nummer

Het verkregen resultaat wordt genoemd Tetraëdrisch aantal orde n, Omdat het is als het verzamelen van driehoekige lagen die een tetraëder vormen, zoals getoond in de volgende animatie.

Figuur 5. De som van N driehoekige getallen komt overeen met de stapel lagen van N, N-1, ..., 1 driehoeken die een reguliere tetraëder vormen. Bron: Wikimedia Commons.

Referenties

1. Camacho J. Een onverwacht uiterlijk van driehoekige nummers. Hersteld van: MassCience.com
2. Claudio. Driehoekige nummers. Hersteld van: eenvoudig nummers. Blogspot. com
3. Wikipedia. Driehoekig nummer. Hersteld van: is.Wikipedia.com
4. Wikipedia. Driehoekig nummer. Opgehaald uit: in.Wikipedia.com
5. Wikipedia. Nummer tretraëdral. Opgehaald uit: in.Wikipedia.com