Wat zijn algebraïsche uitdrukkingen en welke zijn de meest voorkomende?

De algebraïsche uitdrukkingen Het zijn wiskundige termen die getallen en letters bevatten. In combinatie met de symbolen van wiskundige bewerkingen, maken ze het verkrijgen van formules of vergelijkingen, uit beschrijvingen gemaakt door woorden. 

Op hun beurt kunnen die letters worden toegevoegd, afgetrokken, vermenigvuldigd of gedeeld door andere getallen, die expliciet kunnen zijn of ook worden weergegeven door letters.

Figuur 1. Voorbeelden van algebraïsche uitdrukkingen

[TOC]

Waar zijn algebraïsche uitdrukkingen voor?

Bijvoorbeeld de uitdrukking:

2x + 3 

Het is een algebraïsche uitdrukking, waarbij de letter "x" een nummer vertegenwoordigt dat misschien onbekend is of dat verschillende waarden kan nemen.

Wat is het voordeel van het gebruik van een algebraïsche uitdrukking in plaats van te zeggen: "Tweemaal een nummer toegevoegd aan 3"?

Ten eerste neemt algebraïsche expressie minder ruimte in beslag. En dan, als X geen vast getal is, kunnen verschillende waarden worden gegeven aan de "X" om verschillende resultaten van deze uitdrukking te verkrijgen.

Dit staat bekend als de numerieke waarde van algebraïsche expressie.

Als bijvoorbeeld x = 1, is het resultaat 2⋅1 + 3 = 2 + 3 = 5

In plaats daarvan, met x = -2, blijkt de uitdrukking 2⋅ (-2) + 3 = -4 + 3 = -1 te zijn

In een ander type toepassing vertegenwoordigen algebraïsche uitdrukkingen een vergelijking of gelijkheid die moet worden opgelost om de waarde te kennen van het getal dat wordt weergegeven door de brief.

Hier hebben we een eenvoudige lineaire vergelijking:

2⋅x + 3 = 7

De oplossing voor deze vergelijking, die trouwens ook een algebraïsche uitdrukking is, is:

x = 2

Omdat het vermenigvuldigen van 2 bij 2 4 plus 3 geeft, geeft het resultaat: 7. Maar het is gemakkelijker te begrijpen wanneer een algebraïsche uitdrukking wordt gebruikt in plaats van alles te beschrijven met woorden.

Meest voorkomende algebraïsche uitdrukkingen

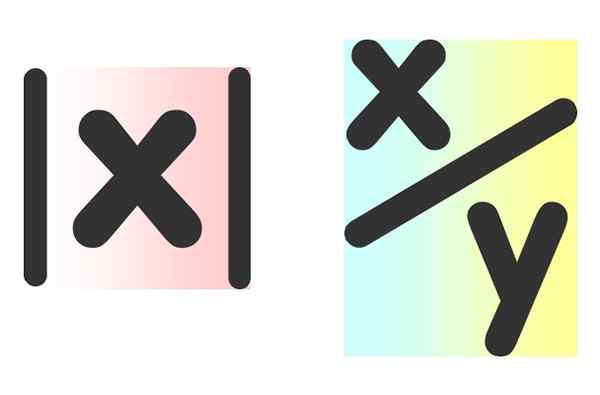Figuur 2. Onbekende hoeveelheden symboliseren vaak met de letters "x" en "y". Links is de absolute waarde van een getal en rechts het quotiënt in twee nummers. Bron: Pixabay.

Algebraïsche uitdrukkingen worden veel gebruikt in wiskunde, wetenschap, economie en administratie.

Hieronder is een lijst met uitdrukkingen die zeer vaak verschijnen in wiskunde en andere onderwerpen, waarin een propositie wordt gevraagd of opgelost.

Het kan u van dienst zijn: Perimeter van de cirkel: hoe u het eruit haalt en formules, opgeloste oefeningen

Meestal wordt een onbekend of onbekend nummer aangeduid als "x", maar we kunnen elke andere alfabetbrief gebruiken zoals overeengekomen.

Er moet ook rekening mee worden gehouden dat het in een algebraïsche uitdrukking meer dan één waarde, onbekend of variabel kan hebben betrokken, dus elke moet een andere brief worden toegewezen.

Lijst met algebraïsche uitdrukkingen

-De dubbele of dubbele van een nummer: 2x

-De duple van een nummer meer eenheden: 2m + 3

-Het derde deel van een nummer: Z/3

-Tweemaal een nummer behalve het derde deel: 2x - x/3

-Het vierkant van een nummer: x²

-Het vierkant van een nummer meer van dat nummer: x² + 2x

-De duple van het vierkant van een nummer: 2x²

-Een koppelnummer: 2n

-Een oneven nummer: 2n + 1

-Drie opeenvolgende nummers: x, (x+1), (x+2)

-Drie opeenvolgende even cijfers: 2n, 2n +2, 2n +4

-Drie opeenvolgende oneven nummers, 2n + 1, 2n + 3, 2n + 5

-Een bepaald nummer toegevoegd aan zijn opeenvolgende: x +(x +1) = 2x +1

-De helft van het opeenvolgende van een geheel getal: (x+1)/2

-De drievoudige van de helft van het vierkant van een nummer: 3. (1/2) x² = (3/2) x²

-De helft van het ene meer nummer van een ander: x/2 + y/3

-Het derde deel van het product tussen het vierkant van een nummer en een ander nummer waaraan de eenheid werd afgetrokken: (1/3) x².(Y-1)

-Een nummer en het tegenovergestelde: a, -a

-Een nummer en zijn inverse: a, 1/a

-De som van een getal met zijn opeenvolgende verheven naar het vierkant: x + (x + 1)²

-Trek 7 af op tweemaal een bepaald aantal hoog aan het vierkant: (2x)² - 7

-Twee nummers die wanneer vermenigvuldigd zijn, geven 24: P.Q = 24

Kan u van dienst zijn: hoekige verplaatsing

-De absolute waarde van een getal: │x│

-Het quotiënt tussen twee nummers: x/y

-De vierkantswortel van het product van twee getallen: √x.En

figuur 3. Deze algebraïsche uitdrukking wordt gelezen als "de vierkantswortel van het product van twee getallen x en y". Bron: Pixabay.

-Het ene nummer dat het andere overschrijdt in 30 eenheden: x = y +30

-Tweemaal een nummer waaraan zijn helft wordt afgetrokken: 2x- x/2

Verbale problemen en hun algebraïsche uitdrukkingen

- Probleem 1

De helft van een koe weegt 100 kg meer dan weegt een kwart van dezelfde koe. Hoeveel weegt de koe?

Antwoord

Voor de algebraïsche uitdrukking van dit probleem noemen we x het gewicht van de koe.

De helft van de koe weegt ½ x. Vierde deel van de koe weegt ¼ x. Ten slotte is de algebraïsche expressie die overeenkomt met: "De helft van de koe weegt 100 kg meer dan een kwart":

½ x = ¼ x + 100

Om te weten hoeveel de koe weegt, moet je de voorwaarden groeperen met X aan de linkerkant en 100 aan de rechterkant laten:

(½ -¼) x = 100

¼x = 100

x = 400 kg

De koe weegt 400 kg.

- Probleem 2

Op een boerderij is het aantal konijnen twee keer zoveel koeien. Als het aantal koeien 10 is. Hoeveel konijnen zijn er?

Antwoord

Als C het aantal konijnen is en V het aantal koeien is, dan is de algebraïsche uitdrukking van de verklaring:

C = 2⋅V

V = 10

Dus het vervangen van de waarde van V in de eerste van de vergelijkingen die deze wordt verkregen:

C = 2 ⋅ 10 = 20

Dat wil zeggen, de boerderij heeft twintig konijnen.

- Probleem 3

Wat is het aantal vermenigvuldigd met zeven en het aftrekken van zes geeft twintig -nine?

Antwoord

Als we dit onbekende nummer X noemen, kan deze algebraïsche uitdrukking worden verhoogd:

Kan u van dienst zijn: Associatieve eigenschap: som, vermenigvuldiging, voorbeelden, oefeningen

7x - 6 = 29

Aan de 6 linkerkant gaat het naar de rechterkant van gelijkheid met een veranderd teken:

7x = 29 + 6 = 35

Hieruit volgt dat x = 35/7 = 5

- Probleem 4

Tweemaal een bepaald getal 13 wordt afgetrokken en 7 is 7. Wat is het nummer?

Antwoord

Als we dat nummer x noemen, is de algebraïsche vergelijking de:

2 x - 13 = 7

Wat is de waarde van 2x ?

Het antwoord is dat 2x moet zijn (13 + 7), zodat wanneer u 13 verwijdert, het is 7.

Dit betekent dat 2x gelijk moet zijn aan 20, dat wil zeggen:

2x = 20

Het nummer x dat vermenigvuldigd met 2 Da 20 is daarom 10,:

x = 10

- Probleem 5

Twee opeenvolgende gehele getallen tellen op 23. Stel een algebraïsche vergelijking voor waarmee het getal het aantal kan bepalen en het kan vinden.

Antwoord

Stel dat de eerste van de getallen n is, dus degene die volgt is n+1 en de som van deze twee is n+(n+1). Het is ook bekend dat de som van de som 23 is, dan wordt de vergelijking geschreven:

n + (n + 1) = 23

De oplossing wordt verkregen eerst de linkerkant van de gelijkheid vereenvoudigen:

2 n + 1 = 23

Dan wordt 2 n door de 1 aan het juiste lid gewist met het gewijzigde teken:

2 n = 23 - 1

Het juiste lid is opgelost:

2 n = 22

Vervolgens, n, die de 2 passeert die het lid van links vermenigvuldigt die het lid van rechts verdeelt:

N = 22/2

En het eindresultaat wordt verkregen:

N = 11

Referenties

1. Baldor, een. Algebra. Midden -Amerikaanse culturele redactionele c.NAAR.
2. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
3. Cimanet. Algebraïsche uitdrukkingen. Hersteld van: cinamet.UOC.Edu
4. Guzman P. Algebraïsche uitdrukkingen. Opgehaald uit: concept van financiering.van
5. Quiz. Algebraïsche uitdrukkingen. Hersteld van: misschien.Opzwepen.Edu
6. Martha. Voorbeelden van algebraïsche uitdrukkingen. Hersteld van: superprof.is