Wat is een geoid?

Hij Geoïde o De figuur van de aarde is het theoretische oppervlak van onze planeet, bepaald door het gemiddelde niveau van de oceanen en met een nogal onregelmatige vorm. Wiskundig wordt het gedefinieerd als het apparatuuroppervlak van het effectieve zwaartekrachtpotentieel van de aarde, op zeeniveau.

Omdat het een denkbeeldig (niet -materiaal) oppervlak is, kruist het continenten en bergen, alsof alle oceanen zijn verbonden door aquatische kanalen die door de terrestrische massa passeren.

Figuur 1. De Geoid. Bron: dat.

De aarde is geen perfecte bol, omdat de rotatie rond zijn as het een soort bal maakt die door de palen is gebakken, met valleien en bergen. Daarom is de sferoïde vorm nog steeds onnauwkeurig.

Diezelfde rotatie voegt een centrifugale kracht toe, waarvan de resulterende of effectieve kracht niet naar het midden van de aarde wijst, maar heeft een bepaald zwaartekrachtpotentieel geassocieerd.

Naast deze geografische ongevallen creëren onregelmatigheden in dichtheid, en daarom houdt de kracht van zwaartekrachtaantrekking in sommige gebieden zeker op om centraal te zijn.

Dat is de reden waarom wetenschappers, beginnend met C. F. Gauss, die in 1828 de oorspronkelijke geoïde bedacht, creëerde een geometrisch en wiskundig model om het aardoppervlak met grotere precisie weer te geven.

Hiervoor wordt een oceaan verondersteld te rusten, zonder getijden of oceaanstromingen en constante dichtheid, waarvan de hoogte dient als een referentie. Dan wordt geacht dat het aardoppervlak zachtjes golvend is, stijgt op plaatsen waar de lokale zwaartekracht groter is en zinkt wanneer het afneemt.

Laten we onder deze omstandigheden de versnelling van effectieve zwaartekracht altijd loodrecht op het oppervlak maken waarvan de punten hetzelfde potentieel hebben en het resultaat is de geoid, die onregelmatig is omdat de apparatuur niet symmetrisch is.

[TOC]

Geoid Physical Foundation

Om de vorm van de geoïde te bepalen, die in de loop van de tijd is verfijnd, hebben wetenschappers veel maatregelen uitgevoerd, rekening houdend met twee factoren:

Kan u van dienst zijn: wat is de netto kracht? (Met voorbeelden)

- De eerste is dat de waarde van G, Het terrestrische zwaartekrachtveld gelijkwaardig aan de versnelling van de zwaartekracht, Het hangt af van de breedtegraad: het is maximaal in de polen en minimum in Ecuador.

- De tweede is dat, zoals we al eerder zeiden, de dichtheid van de aarde niet homogeen is. Er zijn plaatsen waar het toeneemt omdat de rotsen dichter zijn, er is een accumulatie van magma of er is veel land aan de oppervlakte, zoals een berg bijvoorbeeld.

Waar de dichtheid groter is, G Het is ook. Let daar op G Het is een vector en daarom wordt hij met vet aangeduid.

Het landpotentieel van het land

Om de geoid te definiëren, is het potentieel nodig vanwege de zwaartekracht, waarvoor het zwaartekrachtveld moet worden gedefinieerd als de zwaartekracht per massa -eenheid.

Als een testmassa M Het wordt in dit veld geplaatst, de kracht die door de aarde wordt uitgeoefend, is zijn gewicht p = mg, daarom is de grootte van het veld:

Sterkte / massa = p / m = g

We kennen de gemiddelde waarde al: 9.8 m/s² En als de aarde bolvormig zou zijn, zou deze naar het midden worden gericht. Evenzo, volgens de universele zwaartekrachtwet van Newton:

P = GM M /R²

Waarbij m de massa van de aarde is en G de constante van universele zwaartekracht is. Dan de omvang van het zwaartekrachtveld G is:

G = GM/R²

Het lijkt veel op een elektrostatisch veld, zodat u een zwaartekrachtpotentiaal kunt definiëren die analoog is aan de elektrostatische:

V = -gm/r

De constante G is de universele zwaartekrachtconstante. Welnu, de oppervlakken waarop het zwaartekrachtpotentieel altijd dezelfde waarde heeft, worden genoemd Equipotential -oppervlakken En G staat altijd loodrecht op hen, zoals eerder gezegd.

Voor dit specifieke soort potentieel zijn apparatuuroppervlakken concentrische bollen. Het werk dat nodig is om een ​​massa op hen te verplaatsen is nietig, omdat de kracht altijd loodrecht staat op elk pad over het team.

Laterale component van de versnelling van de zwaartekracht

Omdat de aarde niet bolvormig is, moet de versnelling van de zwaartekracht een laterale component G hebben_l Vanwege centrifugale versnelling, veroorzaakt door de rotatiebeweging van de planeet rond zijn as.

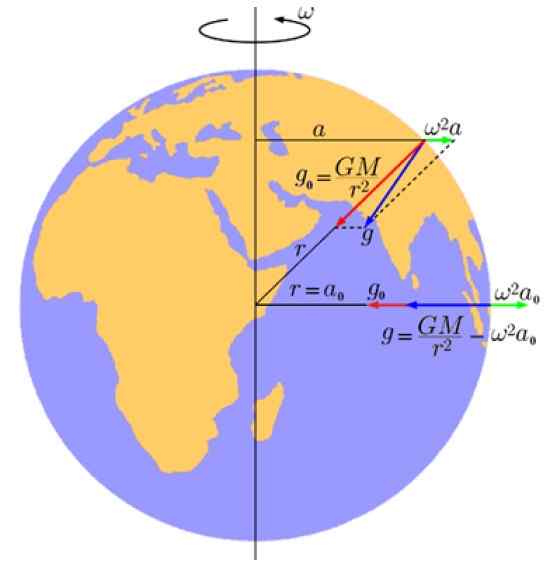
Kan u van dienst zijn: paramagnetisme

In de volgende figuur wordt deze component in groen getoond, waarvan de grootte is:

G_l = Ω²naar

Figuur 2. Effectieve zwaartekrachtversnelling. Bron: Wikimedia Commons. Hightemplar / Public Domain.

In deze vergelijking Ω Het is de hoeksnelheid van rotatie van de aarde en naar Het is de afstand tussen het punt op de aarde, tot een bepaalde breedtegraad en de as.

En in rood is de component die te wijten is aan planetaire gravitatie -aantrekkingskracht:

G_of = GM/R²

Als gevolg hiervan, door vectorly toe te voegen G_of + G_l, Een resulterende versnelling is ontstaan G (in blauw) dat is de ware versnelling van de zwaartekracht van de aarde (of effectieve versnelling) en dat zoals we zien niet precies naar het centrum wijst.

Bovendien hangt de laterale component af van de breedtegraad: het is nul in de polen en daarom is het zwaartekrachtveld maximaal. In Ecuador verzet hij zich tegen de aantrekkingskracht van de zwaartekracht, waardoor de effectieve zwaartekracht wordt verminderd, waarvan de omvang blijft bestaan:

G = GM/R² - Ω²R

Met r = equatoriale radio van de aarde.

Het is nu duidelijk dat de apparatuuroppervlakken van de aarde niet bolvormig zijn, maar dat ze zo'n manier aannemen dat G staat altijd op elk punt loodrecht op hen.

Verschillen tussen geoid en ellipsoïde

Hier is de tweede factor die de variatie van het zwaartekrachtveld van het land beïnvloedt: de lokale variaties van de zwaartekracht. Er zijn plaatsen waar de zwaartekracht toeneemt omdat er meer massa is, bijvoorbeeld in de heuvel in figuur A).

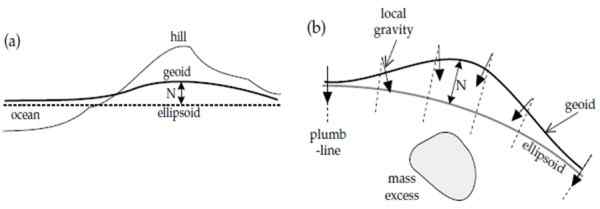figuur 3. Vergelijking tussen Geoid en Ellipsoïde. Bron: Lowrie, W.

Of er is een accumulatie of overtollige massa onder het oppervlak, zoals in B). In beide gevallen is er een verhoging in de geoïde omdat hoe groter de massa, een grotere intensiteit van het zwaartekrachtveld.

In plaats daarvan is de dichtheid lager en bijgevolg zinkt de geoide, zoals we links van figuur A) boven de oceaan zien.

Kan u van dienst zijn: fysieke optiek: geschiedenis, frequente voorwaarden, wetten, applicaties

Uit figuur B) wordt ook opgemerkt dat de lokale zwaartekracht, aangegeven met pijlen, altijd loodrecht staat op het geoïde oppervlak, zoals we hebben gezegd. Dit gebeurt niet altijd met de referentie ellipsoïde.

Geoid -golvingen

In de figuur wordt het ook aangegeven, met een bidirectionele pijl, het hoogteverschil tussen de geoid en de ellipsoïde, die wordt genoemd golving En het wordt aangeduid als n. Positieve golvingen zijn gerelateerd aan overtollige massa en negatieve defecten.

Golvingen zijn bijna nooit hoger dan 200 m. Eigenlijk zijn de waarden afhankelijk van hoe de zeespiegel die als referentie dient, wordt gekozen, omdat sommige landen verschillend kiezen volgens hun regionale kenmerken.

Voordelen om de aarde als een geoid te vertegenwoordigen

-Op de geoïde het effectieve potentieel, het resultaat van het potentieel als gevolg van de zwaartekracht en het centrifugaalpotentieel, is het constant.

-De zwaartekracht werkt altijd loodrecht op de geoïde en de horizon is altijd tangentieel voor hem.

-De Geoid biedt een referentie voor geweldige precisie -cartografische toepassingen.

-Door de geoïde kan seismologen de diepte detecteren waarop aardbevingen optreden.

-De positionering van GPS is afhankelijk van de geoid om als referentie te gebruiken.

-Het oceaanoppervlak is ook parallel aan de geoïde.

-De verhogingen en afdalingen van de geoïde geven de excessen of massa -defecten aan, die de Gravimetrische anomalieën. Wanneer een anomalie wordt gedetecteerd en afhankelijk van de waarde ervan, is het mogelijk om de geologische structuur van de ondergrond af te leiden, althans zelfs bepaalde diepten.

Dit is de basis van gravimetrische methoden in geofysica. Een gravimetrische anomalie kan wijzen op accumulaties van bepaalde mineralen, structuren begraven ondergronds, of ook lege ruimtes. Zoutkoepels in de ondergrond, detecteerbaar door gravimetrische methoden, zijn indicatief in sommige gevallen van de aanwezigheid van olie.

Referenties

1. DAT. Euronews. Gravity's greep op aarde. Hersteld van: YouTube.com.
2. VREUGDE. Geoïde. Hersteld van: YouTube.com.
3. Grieme-Klee, s. Mijnbouwverkenningen: gravimetrie. Hersteld van: geovirtual2.Klet.
4. Lowrie, W. 2007. Fundamentele geofysica. 2e. Editie. Cambridge University Press.
5. NOAA. Wat is de Geoid?. Hersteld van: geodesy.NOAA.Gov.
6. Sheriff, r. 1990000000000000000. Geofysica toepassen. 2e. Editie. Cambridge University Press.