Wat is de evenredigheidsfactor? (Opgeloste oefeningen)

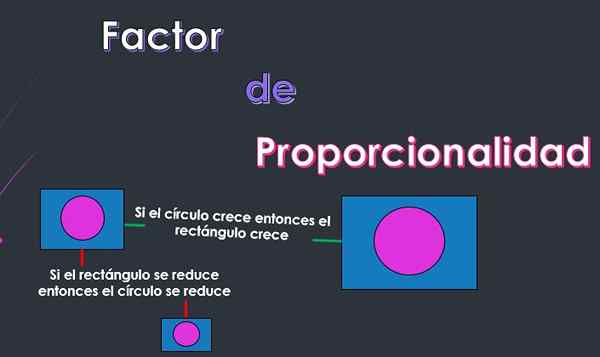
Hij evenredigheidsfactor o Constante van evenredigheid is een getal dat zal aangeven hoeveel het tweede object verandert in relatie tot de verandering die het eerste object heeft geleden.

Als bijvoorbeeld wordt gezegd dat de lengte van een trap 2 meter is en dat de schaduw die dit projecteert 1 meter is (de evenredigheidsfactor is 1/2), dan als de trap wordt gereduceerd tot een lengte van 1 meter, het Shadow zal de lengte verhoudingsgewijs verminderen, daarom zal de lengte van de schaduw 1/2 meter zijn.

Als integendeel de trap wordt verhoogd tot 2.3 meter dan zal de lengte van de schaduw 2 zijn.3*1/2 = 1.15 meter.

Evenredigheid is een constante relatie die kan worden vastgesteld tussen twee of meer objecten, zodat als een van de objecten een verandering lijdt, de andere objecten ook een wijziging zullen ondergaan.

Als er bijvoorbeeld wordt gezegd dat twee objecten evenredig zijn in termen van de lengte, zal het hebben als een object de lengte verhoogt of vermindert, dan zal het andere object ook de lengte van de lengte verhogen of verminderen.

Evenredigheidsfactorconcept

De evenredigheidsfactor is, zoals in het bovenstaande voorbeeld, een constante waarmee men moet vermenigvuldigen om de andere grootte te verkrijgen.

In het vorige geval was de evenredigheidsfactor 1/2, omdat de "x" trap 2 meter gemeten en de schaduw "y" gemeten 1 meter (half). Daarom moet je y = (1/2)*x.

Dus wanneer "x" verandert, dan veranderen "y" ook. Als het "y" is die verandert, zal "x" ook veranderen, maar de evenredigheidsfactor is anders, in dat geval zou het 2 zijn.

Evenredigheidsoefeningen

- Eerste oefening

Juan wil een cake bereiden voor 6 personen. Het recept dat Juan heeft, zegt dat de cake 250 gram bloem, 100 gram boter, 80 gram suiker, 4 eieren en 200 milliliter melk heeft.

Voordat hij de cake begon te bereiden, realiseerde Juan zich dat het recept dat hij heeft voor een cake is voor 4 personen. Wat zou de magnitudes moeten zijn die Juan moet gebruiken?

Oplossing

Hier is de evenredigheid als volgt:

4 personen - 250 g bloem - 100 g boter - 80 g suiker - 4 eieren - 200 ml melk

6 personen -?

De evenredigheidsfactor in dit geval is 6/4 = 3/2, wat kan worden begrepen alsof het eerst wordt gedeeld door 4 om de ingrediënten per persoon te verkrijgen en zich vervolgens met 6 te vermenigvuldigen om de cake voor 6 personen te maken.

Door alle hoeveelheden met 3/2 te vermenigvuldigen, zijn de ingrediënten voor 6 personen zijn:

6 personen - 375 g bloem - 150 g boter - 120 g suiker - 6 eieren - 300 ml melk.

- Tweede oefening

Twee voertuigen zijn identiek, behalve hun banden. De straal van de banden van een voertuig is gelijk aan 60 cm en de straal van de tweede voertuigbanden is gelijk aan 90 cm.

Als je na het nemen van een tournee de hoeveelheid ronden moet geven die de banden met minder straal gaf, was 300 ronden. Hoeveel bochten gaven de grootste radiobanden?

Oplossing

In deze oefening is de evenredigheidsconstante gelijk aan 60/90 = 2/3. Dus als de radiominale banden 300 ronden gaven, gaven de banden met de hoogste radio 2/3*300 = 200 ronden.

- Derde oefening

Het is bekend dat 3 werknemers een muur van 15 square -meter in 5 uur hebben geverfd. Hoeveel kunnen ze 7 werknemers in 8 uur schilderen?

Oplossing

De gegevens in deze oefening zijn:

3 werknemers - 5 uur - 15 m² muur

En wat hij zich afvraagt ​​is:

7 werknemers - 8 uur -- ? M² muur.

U kunt vragen hoeveel 3 werknemers over 8 uur zouden schilderen? Om dit te weten, wordt de gegevensrij verstrekt door de verhoudingsfactor 8/5 vermenigvuldigd. Dit laat als gevolg hiervan zien:

3 werknemers - 8 uur - 15*(8/5) = 24 m² muur.

Nu wilt u weten wat er gebeurt als het aantal werknemers wordt verhoogd tot 7. Om te weten welk effect het produceert de hoeveelheid muur die wordt geschilderd door factor 7/3. Dit geeft de uiteindelijke oplossing:

7 werknemers - 8 uur - 24*(7/3) = 56 m² muur.

Referenties

1. Cofré, een., & Tapia, l. (negentienvijfennegentig). Hoe wiskundige logische redenering te ontwikkelen. Universitair hoofdartikel.
2. Geavanceerde Telerasporte -fysica. (2014). Edu nasz.
3. Giancoli, D. (2006). Fysica -volume I. Pearson Education.
4. Hernández, J. D. (S.F.)). Wiskunde notebook. Drempelwaarde.
5. Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Wiskunde 1 september. Drempelwaarde.
6. Neuhauser, c. (2004). Wiskunde voor wetenschap. Pearson Education.
7. Peña, m. D., & Muntaner, aan. R. (1989). Fysische chemie. Pearson Education.
8. Segovia, B. R. (2012). Wiskundige activiteiten en spelletjes met Miguel en Lucía. Baldomero Rubio Segovia.
9. Tocci, r. J., & Widmer, n. S. (2003). Digitale systemen: principes en toepassingen. Pearson Education.