Trigonometrische limieten hoe ze op te lossen, opgeloste oefeningen

De trigonometrische limieten Het zijn limieten van functies zodanig dat deze functies worden gevormd door trigonometrische functies.

Er zijn twee definities waarvan bekend moet worden dat ze begrijpen hoe de berekening van een trigonometrische limiet wordt uitgevoerd. Deze definities zijn:

- Limiet van een "F" -functie wanneer "X" de neiging heeft "B": het bestaat uit het berekenen van de waarde waarbij F (x) nadert als "X" nadert "B", zonder te beweren "B".

- Trigonometrische functies: trigonometrische functies zijn de sinus-, cosinus- en raaklijnfuncties, aangegeven door SIN (X), COS (X) en TAN (X).

De andere trigonometrische functies worden verkregen uit de drie hierboven genoemde functies.

Functie limieten

Om het concept van een functielimiet te verduidelijken, zullen we doorgaan met het tonen van enkele voorbeelden met eenvoudige functies.

- De limiet van f (x) = 3 wanneer "x" neigt naar "8" is gelijk aan "3", omdat de functie altijd constant is. Het maakt niet uit hoeveel "x" waard is, de waarde van f (x) zal altijd "3" zijn.

- De limiet van f (x) = x-2 wanneer "x" neigt naar "6" is "4". Sinds wanneer "X" dicht bij "6" is, benadert "X-2" "6-2 = 4".

- De limiet van g (x) = x² wanneer "x" neigt naar "3" is gelijk aan 9, omdat wanneer "x" "3" nadert, "x²" nadert "3² = 9".

Zoals in de vorige voorbeelden kan worden opgemerkt, bestaat het berekenen van een limiet bij het evalueren van de waarde waartoe "x" in de functie neigt, en het resultaat zal de waarde van de limiet zijn, hoewel dit alleen waar is voor continue functies.

Zijn er meer gecompliceerde limieten?

Het antwoord is ja. De vorige voorbeelden zijn de eenvoudigste voorbeelden van limieten. In berekeningsboeken zijn de belangrijkste limietoefeningen die die een onbepaaldheid van type 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 en (∞)^0 genereren.

Kan u van dienst zijn: Pythagorische identiteiten: demonstratie, bijvoorbeeld oefeningen

Deze uitdrukkingen worden onbeperkingen genoemd, omdat het uitdrukkingen zijn die wiskundig logisch zijn.

Daarnaast kan, afhankelijk van de functies die betrokken zijn bij de oorspronkelijke limiet, het resultaat verkregen bij het oplossen van de onbeperkingen in elk geval verschillend zijn.

Voorbeelden van eenvoudige trigonometrische limieten

Om limieten op te lossen, is het altijd erg handig om de grafieken van de betrokken functies te kennen. Hieronder staan ​​de grafieken van de sinus, cosinus en raakwerkfuncties.

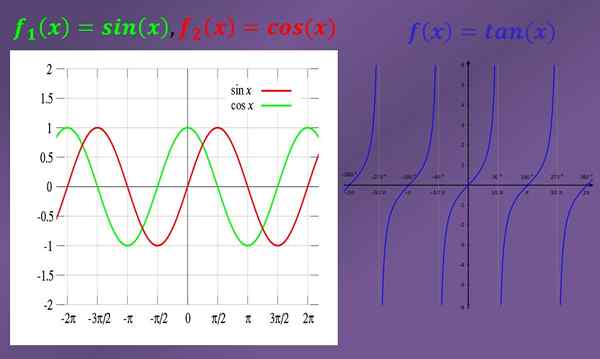
Enkele voorbeelden van eenvoudige trigonometrische limieten zijn:

- Bereken de zonder (x) limiet wanneer "x" de neiging heeft "0".

Als je de grafiek ziet, kun je zien dat als "X" "0" nadert (zowel links als rechts), de afbeelding van de borst ook "0" nadert. Daarom is de limiet van sin (x) wanneer "x" de neiging heeft "0" "0" is.

- Bereken de grens van cos (x) wanneer "x" de neiging heeft "0".

Het observeren van de grafiek van de cosinus is te zien dat wanneer "x" dicht bij "0" is, de grafiek van de cosinus dicht bij "1" is. Dit houdt in dat de grens van cos (x) wanneer "x" neigt naar "0" gelijk is aan "1".

Er kan een limiet bestaan ​​(een getal zijn), zoals het geval is in de vorige voorbeelden, maar het kan ook gebeuren dat deze niet bestaat zoals in het volgende voorbeeld wordt getoond.

- De limiet van tan (x) wanneer "x" neigt naar "π/2" aan de linkerkant is gelijk aan "+∞", zoals te zien is in de afbeeldingen. Aan de andere kant is de limiet van tan (x) wanneer "x" neigt naar "-π/2" aan de rechterkant gelijk aan "-∞".

Trigonometrische beperkingen identiteiten

Twee zeer bruikbare identiteiten wanneer trigonometrische limieten worden berekend, zijn:

Kan u van dienst zijn: niet -lineaire programmering: methoden en oefeningen

- De limiet van "sin (x)/x" wanneer "x" neigt naar "0" is gelijk aan "1".

- De limiet van "(1-cos (x))/x" wanneer "x" neigt naar "0" is gelijk aan "0".

Deze identiteiten worden heel vaak gebruikt wanneer u een soort onbepaaldheid heeft.

Opgeloste oefeningen

Los de volgende limieten op met behulp van de hierboven beschreven identiteiten.

- Oefening 1

Bereken de limiet van "f (x) = zonder (3x)/x" wanneer "x" de neiging heeft "0".

Als de "F" -functie wordt geëvalueerd in "0", wordt een onbepaaldheid van type 0/0 verkregen. Daarom moeten we proberen deze onbepaaldheid op te lossen met behulp van de beschreven identiteiten.

Het enige verschil tussen deze limiet en identiteit is het nummer 3 dat binnen de sinusfunctie verschijnt. Om de identiteit toe te passen, moet de functie "F (x)" als volgt worden herschreven "3*(zonder (3x)/3x)". Nu zijn zowel het borstargument als de noemer gelijk.

Dus wanneer "X" de neiging heeft om "0" te gebruiken, is het gebruik van identiteit "3*1 = 3". Daarom is de limiet van f (x) wanneer "x" neigt naar "0" gelijk aan "3".

- Oefening 2

Bereken de limiet van "g (x) = 1/x - cos (x)/x" wanneer "x" de neiging heeft "0".

Wanneer "x = 0" wordt vervangen in g (x) een onbepaaldheid van het type ∞ -∞. Om het op te lossen, worden de breuken afgetrokken, wat een resultaat geeft "(1-cos (x))/x".

Nu, door de tweede trigonometrische identiteit toe te passen, is de limiet van G (x) dat "x" de neiging heeft "0" gelijk is aan 0.

- Oefening 3

Bereken de limiet van "h (x) = 4tan (5x)/5x" wanneer "x" neigt naar "0".

Nogmaals, als h (x) wordt geëvalueerd in "0" wordt een onbepaaldheid van type 0/0 verkregen.

Herschrijven als (5x) als zonder (5x)/cos (5x) Het blijkt dat H (x) = (zonder (5x)/5x)*(4/cos (x))).

Het kan u van dienst zijn: ingeschreven hoek van een cirkel: definitie, stellingen, voorbeelden

Met behulp van dat de limiet van 4/cos (x) wanneer "x" de neiging heeft "0" is gelijk aan "4/1 = 4" en de eerste trigonometrische identiteit wordt verkregen dat de limiet van h (x) wanneer "x" neigt "0" is gelijk aan "1*4 = 4".

Observatie

Trigonometrische limieten zijn niet altijd gemakkelijk op te lossen. In dit artikel werden alleen basisvoorbeelden getoond.

Referenties

1. Fleming, W., & Varberg, D. EN. (1989). Prealculus wiskunde. Prentice Hall PTR.
2. Fleming, W., & Varberg, D. EN. (1989). Precalculus Wiskunde: een probleemoplossende aanpak (2, geïllustreerd ED.)). Michigan: Prentice Hall.
3. Fleming, W., & Varberg, D. (1991). Algebra en trigonometrie met analytische geometrie. Pearson Education.
4. Larson, r. (2010). Prealculus (8 ed.)). Cengage leren.
5. Loyaal, j. M., & Viloria, n. G. (2005). Platte analytische geometrie. Mérida - Venezuela: Venezolaanse redactie C. NAAR.
6. Pérez, c. D. (2006). Prequalculus. Pearson Education.
7. Purcell, E. J., Varberg, D., & Rigdon, s. EN. (2007). Berekening (Negende ed.)). Prentice Hall.
8. Saenz, J. (2005). Differentiële berekening met vroege transcendente functies voor wetenschap en engineering (Tweede editie ed.)). Hypotenuse.
9. Scott, C. NAAR. (2009). Cartesiaanse vlakke geometrie, deel: Analytical Conics (1907) (Herdruked ed.)). Bliksembron.
10. Sullivan, m. (1997). Prequalculus. Pearson Education.