Wat is dynamisch evenwicht? (Met voorbeeld)

Hij dynamisch evenwicht Het is de toestand waarin een mobiel object idealiter wordt weergegeven als een deeltje wanneer de beweging uniform is rechtlijnig. Dit fenomeen treedt op wanneer de som van externe krachten die erop werken wordt geannuleerd.

Meestal wordt aangenomen dat als er geen netto of resulterende kracht op een object is, rust het enige mogelijke gevolg is. Of ook dat een lichaam in evenwicht is, er zou geen kracht moeten zijn.

Figuur 1. Deze kat beweegt in dynamisch evenwicht als het het doet met constante snelheid. Bron: Pixabay.

Eigenlijk is het evenwicht afwezigheid van versnelling, en daarom is de constante snelheid perfect mogelijk. De kat in de figuur kan zonder versnelling bewegen.

Een object dat een uniforme cirkelvormige beweging bezit, is niet in dynamisch evenwicht. Hoewel de snelheid ervan constant is, is er een versnelling gericht op het midden van de omtrek die deze in het traject houdt. Deze versnelling is verantwoordelijk voor het correct veranderen van de snelheidsvector.

Null -snelheid is een bepaalde situatie van de balans van een deeltje, gelijk aan het bevestigen dat het object in rust is.

Wat betreft het beschouwen van objecten als een deeltje, het is een zeer nuttige idealisatie bij het beschrijven van hun wereldwijde beweging. De mobiele objecten die ons omringen, bestaan ​​eigenlijk uit een groot aantal deeltjes waarvan de individuele studie omslachtig zou zijn.

[TOC]

Het superpositieprincipe

Dit principe maakt het mogelijk om de werking van meerdere krachten op een object te vervangen door een equivalent dat de resulterende krachtkoud of netto kracht FN wordt genoemd en dat is in dit geval nietig:

F1 +F2 +F3 +.. . = Fr = 0

Waar F1, F2, F3 .. ., Fi zijn de verschillende krachten die op het lichaam werken. Sumory notatie is een compacte manier om het uit te drukken:

Zolang een onevenwichtige kracht niet ingrijpen, kan het object voor onbepaalde tijd worden bewogen met constante snelheid, omdat alleen een kracht deze panorama kan veranderen.

In termen van de componenten van de resulterende kracht wordt de dynamische evenwichtstoestand van een deeltje als volgt uitgedrukt: Fx = 0; Fy = 0; Fz = 0.

Rotatie- en balansvoorwaarden

Voor het deeltjesmodel is voorwaarde FR = 0 voldoende balansgarantie. Wanneer rekening wordt gehouden met de afmetingen van de onderzochte mobiel, is er echter de mogelijkheid dat het object kan roteren.

De rotatiebeweging impliceert het bestaan ​​van een versnelling, daarom zijn de roterende lichamen niet in dynamisch evenwicht. De draai aan een lichaam heeft niet alleen de deelname van een kracht nodig, maar het is noodzakelijk om de handige site toe te passen.

Om het te controleren, kunt u een dunne staaf van lengte plaatsen op een oppervlak vrij van wrijving, zoals een ijzig oppervlak of een zeer gepolijste spiegel of glas. De normale balans op het gewicht verticaal, en bij het aanbrengen van twee krachten F1 en F2 van dezelfde grootte, volgens het diagram van de volgende figuur, wat gebeurt er:

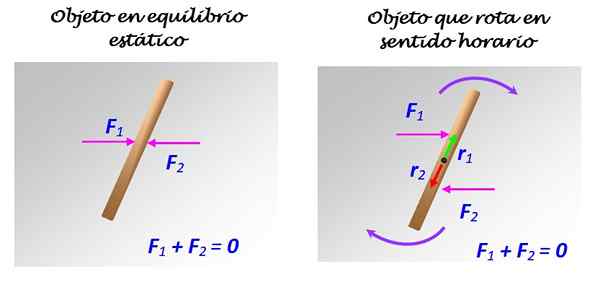Figuur 2. Een staaf op een oppervlak zonder wrijving kan al dan niet in evenwicht zijn, afhankelijk van hoe krachten 1 en 2 worden toegepast. Bron: zelf gemaakt.

Als F1 en F2 van toepassing zijn zoals aan de linkerkant, met een gemeenschappelijke werklijn, blijft de staaf in rust. Maar als F1 en F2 van toepassing zijn zoals aan de rechterkant, met verschillende handelslijnen, hoewel parallel, vindt er een rotatie plaats in een schema, rond de as die door het midden gaat.

In dit geval vormen F1 en F2 een paar krachten of gewoon een paar.

Koppel of moment van kracht

Het effect van het koppel is om een ​​rotatie te produceren op een uitgebreid object zoals de voorbeeldstaaf. De vectorgrootte wordt opgeladen koppel of ook een moment van een kracht genoemd. Het wordt aangeduid als τ en wordt berekend door:

τ = r x f

In deze uitdrukking is F de uitgeoefende kracht en R is de vector die van de rotatieas naar het toepassingspunt van de kracht gaat (zie figuur 2). De richting van τ staat altijd loodrecht op het vlak waar f en r liggen en zijn eenheden in het internationale systeem zijn n.M.

Voor het voorbeeld is de richting van de momenten geproduceerd door F1 en F2 in de richting van de krant, volgens de regels van het vectorproduct.

Hoewel de krachten elkaar annuleren, doen hun koppels dat niet. En het resultaat is de getoonde rotatie.

Evenwichtsvoorwaarden voor een uitgebreid object

Dit zijn twee voorwaarden waaraan moet worden voldaan om het evenwicht van een uitgebreid object te garanderen:

Opgelost voorbeeld

Je hebt een lade of kofferbak die 16 kg-F weegt, die met constante snelheid door een hellend vlak glijdt. De haak van de wiggende helling is θ = 36º. Antwoord:

a) Wat is de grootte van de dynamische wrijvingskracht die nodig is om de romp met constante snelheid te schuiven?

b) Hoeveel is de kinetische wrijvingscoëfficiënt?

c) Als de hoogte h van het hellende vlak 3 meter is, zoek dan de afdaling van de romp wetende dat het 4 seconden duurt om de grond te bereiken.

Oplossing

De kofferbak kan worden behandeld alsof het een deeltje is. Daarom zullen de krachten op een punt van toepassing zijn op ongeveer in het midden, waarop al zijn massa kan worden aangenomen. Het is tot nu toe dat de track zal worden gevolgd.

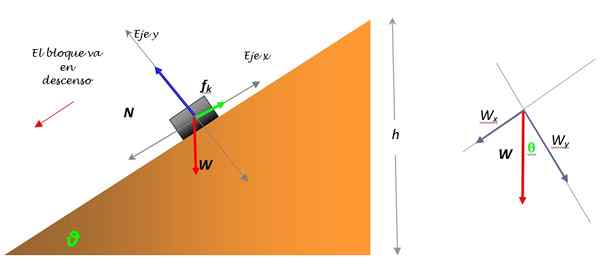figuur 3. Vrij lichaamsdiagram voor de kofferbak die bergafwaarts glijdt en de afbraak van gewicht (rechts). Bron: zelf gemaakt.

Het gewicht W is de enige kracht die niet op een van de coördinaatassen valt en moet worden verbroken in twee componenten: WX en WY. Deze ontleding wordt getoond in het schema (figuur 3).

Het is ook handig om het gewicht door te geven aan eenheden van het internationale systeem, waarvoor het voldoende is om zich met 9 te vermenigvuldigen.8:

Wy = w.cosθ = 16 x 9.8 x cos 36º n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x sin 36º = 92.2 n

Sectie A

Gedurende de horizontale as zijn de horizontale component van het WX -gewicht en de FK -dynamische of kinetische wrijvingskracht, die zich verzet tegen de beweging.

Het kiezen van de positieve zin in de richting van de beweging, het is gemakkelijk om op te merken dat het WX verantwoordelijk is voor het blok om bergafwaarts te gaan. En omdat de wrijving tegengewerkt is, in plaats van snel wegglippen, heeft het blok de mogelijkheid om constant bergafwaarts te glijden.

De eerste evenwichtstoestand is voldoende, omdat we de romp als een deeltje behandelen, wat wordt verzekerd in de verklaring die in dynamisch evenwicht is:

Wx - fk = 0 (er is geen versnelling in het horizontale adres)

FK = 92.2 n

Sectie B

De grootte van dynamische wrijving is constant en wordt gegeven door fk = μk n. Dit betekent dat de dynamische wrijvingskracht evenredig is aan normaal en de grootte hiervan is vereist om de wrijvingscoëfficiënt te kennen.

Als we het vrije lichaamsdiagram observeren, is het te zien dat we op de verticale as de normale kracht n hebben, die de wig op de stam uitoefent en naar boven wordt gericht. Ze is in balans met de verticale component van het gewicht WY. Selecteren als een positieve zin en gebruik maken van de tweede wet van Newton en de evenwichtsstatusresultaten:

N - wy = 0 (er is geen beweging langs de verticale as)

Daarom:

N = wy = 126.9 n

fk = μk n

μk = fk / n = 92.2/126.9 = 0.73

Sectie C

De totale afstand afgelegd door de kofferbak van de bovenkant van de wig naar de grond wordt gevonden door trigonometrie:

d = h/sin 36º = 3/sin 36º m = 5.1 m.

Om de snelheid te berekenen, wordt de definitie voor uniforme rechtlijnige beweging gebruikt:

V = d/t = 5.1 m/4 s = 1.3 m/s

Referenties

1. Rex, a. 2011. Fundamentals of Physics. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren. 120 - 124.
3. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9na ed. Cengage leren. 99-112.
4. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Natuurkunde. Addison Wesley. 148-164.