Coplanares Points -vergelijking, voorbeeld en opgeloste oefeningen

De Coplanares -punten Ze behoren allemaal tot hetzelfde vliegtuig. Twee punten zijn altijd coplanares, omdat deze punten een lijn definiëren waarmee platte oneindigheden passeren. Vervolgens behoren beide punten tot elk van de plannen die door de lijn gaan en zullen daarom altijd coplanares zijn.

Aan de andere kant definiëren drie punten een enkel vlak, waarvan het wordt gevolgd dat drie punten altijd coplanares zullen zijn voor het vliegtuig dat ze bepalen.

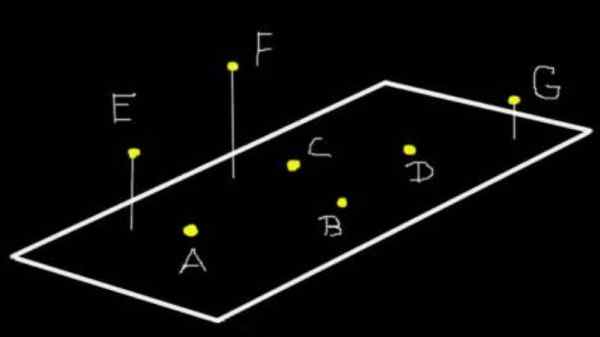
Figuur 1. A, b, c en d ze zijn coplanares van het vlak (ω). E, F en G zijn geen coplanares A (ω) maar als ze coplanares zijn naar het vlak dat drie definiëren. Bron: f. Zapata.

Meer dan drie punten kunnen coplanar zijn of niet. In figuur 1 zijn bijvoorbeeld punten A, B, C en D coplanares van het vlak (ω). Maar e, f en g zijn geen coplanares a (ω), hoewel ze coplanares zijn naar het vlak dat drie definiëren.

[TOC]

Vergelijking van een vlak gegeven drie punten

De vergelijking van een vlak bepaald door drie bekende punten A, B, C is een wiskundige relatie die garandeert dat elk punt P van generieke coördinaten (x, y, z) die de vergelijking vervult, behoort tot het vlak. 

De vorige verklaring is gelijk aan te zeggen dat als p van coördinaat (x, y, z) voldoet aan de vliegtuigvergelijking, dan het punt zal zijn om te copatar met de drie punten a, b, c die het vliegtuig bepaalde.

Laten we beginnen met het vinden van de vergelijking van het vliegtuig met het vinden van de vectoren Aab En AC:

Aab = [Bx - ax, door - ay, bz - az]

AC = [Cx - ax, cy - ay, cz - az]

Het vectorproduct Aab X AC Het resulteert in een loodrechte of normale vector in het vlak bepaald door punten A, B, C.

Een elk punt van coördinaten (x, y, z) behoort tot het vlak als het waar is dat de vector AP staat loodrecht op de vector Aab X AC, dat is gegarandeerd als het wordt vervuld:

Kan u van dienst zijn: Decagon: regelmatig, onregelmatig, eigenschappen, voorbeelden

AP • (AB X AC) = 0

Dit is gelijk aan te zeggen dat het drievoudige product van AP, Aab En AC Wees nietig. De vorige vergelijking kan op een Matrix -manier worden geschreven:

Voorbeeld

Laat punten A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) en D (naar, 0, 1). Welke waarde zou moeten hebben naar zodat de vier punten coplanares zijn?

Oplossing

Om de waarde van A te vinden, is het noodzakelijk dat het punt D deel uitmaakt van het vlak bepaald door A, B en C, wat is gegarandeerd als de vliegtuigvergelijking bijeenkomt.

De determinant ontwikkelen die we hebben:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2a -8 + 6 = -2a -2 = 0

De vorige vergelijking geeft dat aan A = -1 Om gelijkheid te vervullen. Met andere woorden, de enige manier waarop dat punt D (naar, 0.1) Wees coplanar met punten A, B en C is dat naar Valga -1. Anders zal het niet Coplanar zijn.

Opgeloste oefeningen

- Oefening 1

Een vlak snijdt respectievelijk de Cartesiaanse assen x, y, z in 1, 2 en 3. De kruising van genoemde vlak met de assen bepaalt punten A, B en C. Zoek de DZ -component van een punt D, waarvan de Cartesiaanse componenten zijn:

 D (-Dz, Dz+1, Dz) 

Op voorwaarde dat D coplanar is met punten A, B en C. 

Oplossing

Wanneer de onderscheppingen van een vlak met de Cartesiaanse assen bekend zijn, kan de segmentale vorm van de vlakvergelijking worden gebruikt:

x/1 + y/2 + z/3 = 1

Aangezien punt D tot het vorige vlak moet behoren, moet u:

-Dz/1 + (dz + 1)/2 + dz/3 = 1

Het is te zeggen:

-Dz + dz/2 + ½ + dz/3 = 1

Dz (-1 + ½ + ⅓) = ½ 

Dz (-1/6⅙) = ½ 

Dz = -3 

Uit het bovenstaande volgt dat punt D (3, -2, -3) is om te koppelen met punten A (1, 0, 0); B (0, 2, 0) en C (0, 0, 3).

Het kan u van dienst zijn: driehoekige overeenkomstcriteria

- Oefening 2

Bepaal of punten A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) en D (2, 3, 1) zijn Coplanares.

Oplossing

We vormen de matrix waarvan de rangen de coördinaten zijn van D-A, B-A en C-A. Dan wordt de determinant berekend en wordt het geverifieerd of nul al dan niet.

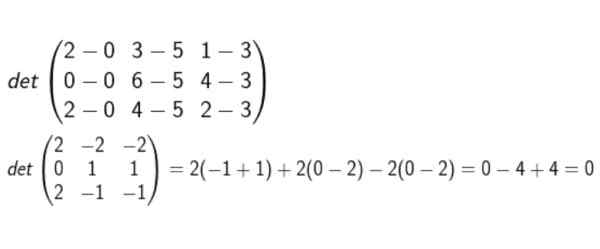
Na het uitvoeren van alle berekeningen wordt geconcludeerd dat ze coplanares zijn.

- Oefening 3

Twee lijnen worden in de ruimte gegeven. Een van hen is de lijn (R) waarvan de parametrische vergelijking is:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

En de andere is de lijn (en) waarvan de vergelijking is:

(S): x + 2 y = 1; Z = -1

Toon aan dat (r) en (s) ze coplanarium recht zijn, dat wil zeggen dat ze zich in hetzelfde vlak bevinden.

Oplossing

Laten we willekeurig twee punten op de lijn (R) en twee op de lijn (en) beginnen:

Rechte (r): λ = 0; A (1, 1, 1) en λ = 1; B (3, 0, 1)

Laten we doen x = 0 op de lijn (s)=> y = ½; C (0, ½, -1). En aan de andere kant, als we dat doen y = 0 => x = 1; D (1, 0, -1).

Dat wil zeggen, we hebben punten A en B genomen die behoren tot de lijn (R) en de punten C en D die tot de lijn (s) behoren. Als die punten coplanares zijn, zullen de twee lijnen ook zijn.

Nu kiezen we ervoor om te wijzen op hoe de pivot en dan vinden we de coördinaten van de vectoren Aab, AC En ADVERTENTIE. Op deze manier krijg je:

B - A: (3-1, 0 -1, 1 - 1) => Aab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

D -a: (1-1, 0 -1, -1 -1) => ADVERTENTIE= (0, -1, -2)

De volgende stap is om de determinant te bouwen en te berekenen waarvan de eerste rij de vectorcoëfficiënten is Aab, De tweede rij zijn die van AC en de derde rij die van de vector ADVERTENTIE:

Kan u van dienst zijn: miletus Een dergelijke stelling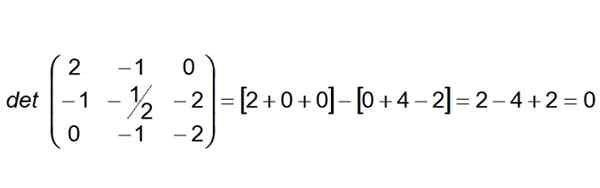

Aangezien de bepalende factor nul blijkt te zijn, kunnen we concluderen dat de vier punten coplanarios zijn. Bovendien kan worden gezegd dat lijnen (R) en (s) ook Coplanares zijn.

- Oefening 4

De lijnen (r) en (s) zijn coplanares, zoals aangetoond in oefening 3. Vind de vergelijking van het vlak dat ze bevat.

Oplossing

Punten A, B, C definiëren dat vlak volledig, maar we willen opleggen dat elk punt x van coördinaten (x, y, z) tot hetzelfde behoort.

X - a: (x -1, y -1, z - 1) => Bijl= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => Aab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

Zodat x behoort tot het vlak gedefinieerd door a, b, c en waarin de lijnen (r) en (s) zijn ingesloten, is het noodzakelijk dat de determinant gevormd op de eerste rij wordt geannuleerd door de componenten van Bijl, in de tweede door die van Aab En in de derde door die van AC:

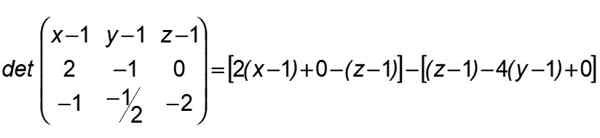
Volgens dit resultaat groeperen we op deze manier:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

En onmiddellijk wordt gezien dat het zo kan worden herschreven:

x - 1 + 2y - 2 - z + 1 = 0

Daarom is x + 2y - z = 2 de vergelijking van het vlak dat de lijnen (r) en (s) bevat.

Referenties

1. Fleming, W. 1989. Prealculus wiskunde. Prentice Hall PTR.
2. Kolman, B. 2006. Lineaire algebra. Pearson Education.
3. Loyaal, j. M. 2005. Platte analytische geometrie. Mérida - Venezuela: Venezolaanse redactie C. NAAR.
4. Navarro, Rocio. De vectoren. Hersteld van: boeken.Google.co.gaan.
5. Pérez, c. D. 2006. Voorzetting. Pearson Education.
6. Prenowitz, W. 2012. Basisconcepten van geometrie. Rowman & Littlefield.
7. Sullivan, m. 1997. Voorzetting. Pearson Education.