Interne en externe geconjugeerde hoeken voorbeelden, oefeningen

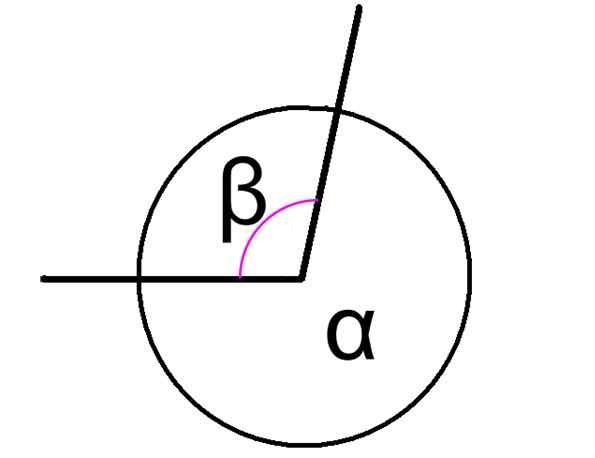
De geconjugeerde hoeken Zij zijn degenen die worden toegevoegd als gevolg van 360 °, ongeacht of deze hoeken aangrenzend zijn of niet. Figuur 1 toont twee geconjugeerde hoeken, aangeduid als α en β.

In dat geval hebben de hoeken α en β van de figuur een gemeenschappelijk hoekpunt en zijn hun zijkanten gebruikelijk, daarom zijn ze aangrenzend. De relatie tussen hen wordt als volgt uitgedrukt:

α + β = 360º

Figuur 1. Twee geconjugeerde centrale hoeken, som. Bron: Wikimedia Commons. Geen machine-leesbare auteur verstrekt. Thiago r Ramos veronderstelde (op basis van auteursrechtclaims). [CC BY-SA 3.0 (http: // creativeCommons.Org/licenties/by-sa/3.0/)] Het is een classificatie van de hoeken door zijn som. Andere belangrijke definities zijn onder meer Complementaire hoeken, waarvan de som 90 º is en de Aanvullende hoeken, die in totaal 180 º.

Aan de andere kant, laten we nu rekening houden met twee parallelle lijnen gesneden door een Secant, wiens dispositie dan wordt getoond:

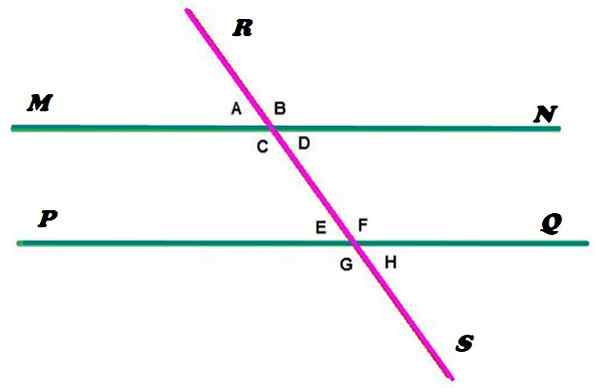
Figuur 2. Parallelle lijnen gesneden door een secant. Bron: f. Zapata.

De MN- en PQ -lijnen zijn parallel, terwijl de RS -lijn droogt, parallellen in twee punten kruisen. Zoals te zien is, bepaalt deze configuratie de vorming van 8 hoeken, waaraan het is aangeduid met kleine letters.

Welnu, volgens de definitie die in het begin wordt gegeven, zijn hoeken A, B, C en D geconjugeerd. En op dezelfde manier zijn ze E, F, G en H, omdat beide gevallen worden vervuld dat:

A+B+C+D = 360º

EN

E+F+G+H = 360º

Voor deze configuratie zijn twee hoeken geconjugeerd als ze aan dezelfde kant zijn ten opzichte van de RS -drooglijn en beide zijn intern of extern. In het eerste geval is er sprake van hoeken Interne conjugaten, Terwijl ze in het tweede zijn, staan ​​ze in hoeken externe conjugaat.

[TOC]

Voorbeelden

In figuur 2 zijn de externe hoeken die die buiten het gebied zijn gescheiden door de MN- en PQ -lijnen, het zijn de hoeken A, B, G en H. Terwijl de hoeken tussen de twee lijnen C, D, E en F zijn.

Kan u van dienst zijn: Coplanares -punten: vergelijking, voorbeeld en opgeloste oefeningen

Nu is het noodzakelijk om te analyseren welke hoeken links staan ​​en welke rechts van de Secant.

Links van Rs zijn hoeken A, C, E en G. En aan de rechterkant zijn B, D, F en H.

We gaan onmiddellijk door met het bepalen van de paren van geconjugeerde hoeken, volgens de definitie in de vorige sectie:

-A en G, extern en links van Rs.

-D en F, intern en rechts van Rs.

-B en H, extern en rechts van Rs.

-C en E, intern en links van Rs.

Eigenschap van geconjugeerde hoeken tussen parallelle lijnen

De geconjugeerde hoeken tussen parallelle lijnen zijn aanvullend, dat wil zeggen dat hun som gelijk is aan 180 °. Op deze manier wordt voor figuur 2 het volgende vervuld:

A + G = 180º

D + F = 180º

B + H = 180º

C + E = 180º

De bijbehorende hoeken paren voor parallelle lijnen

Zij zijn die die aan dezelfde kant van de drooglijn staan, ze zijn niet aangrenzend en een van hen is intern en de andere is extern. Het is belangrijk om ze te visualiseren, omdat hun maatregel hetzelfde is, omdat ze tegenover hoeken zijn door het hoekpunt.

Terugkerend naar figuur 2, worden de overeenkomstige hoeken geïdentificeerd als:

-A en E

-C en G

-B en F

-D en H

Interne hoeken van een vierhoek

De vierhoekige vierzijdige polygonen zijn 4 -zijdige polygonen, inclusief het vierkant, de rechthoek, de trapeze, het parallellogram en de rhombus, bijvoorbeeld, bijvoorbeeld. Ongeacht zijn vorm, in elk van hen wordt vervuld dat de som van zijn interne hoeken 360º is, daarom voldoen ze aan de definitie die aan het begin wordt gegeven.

Laten we eens kijken naar enkele voorbeelden van vierhuizen en hoe de waarde de interne hoeken te berekenen volgens de informatie van de voorgaande secties:

Kan u van dienst zijn: wat zijn de 7 elementen van de omtrek?

Voorbeelden

a) Drie van de hoeken van een vierhoekige maat 75º, 110º en 70º. Hoeveel moet de resterende hoek meet?

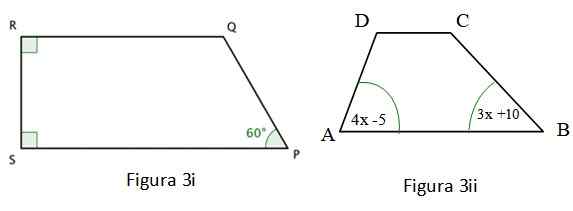
b) Zoek de waarde van de hoek ∠Q in figuur 3 i.

c) Bereken hoeveel meet de hoek ∠A van figuur 3 ii.

Oplossing voor

Laat α de ontbrekende hoek zijn, het is vervuld dat:

α + 75 º + 110º + 70º = 360 → α = 105º

Oplossing B

Figuur 3i getoond is een Trapezoid En twee van zijn interne hoeken zijn recht, die zijn opgemerkt met een kleurenkantje in de hoeken. Voor deze vierhoek is het volgende geverifieerd:

∠r + ∠s + ∠p + ∠q = 360º; ∠S = ∠r = 90º; ∠p = 60º

Daarom:

∠ q = 2 x 90º + 60º = 240º

Oplossing C

De vierhoek van figuur 3 II is ook een trapeze, waarvoor het volgende is vervuld:

∠a + ∠b + ∠c + ∠d = 360º

Daarom:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

X = 25

Om de in de verklaring gevraagde hoek te bepalen, wordt gebruikt dat ∠a = 4x - 5. Het vervangen van de waarde van x eerder berekende wordt gevolgd dat ∠a = (4 × 25) -5 = 95º

Opdrachten

- Oefening 1

Wetende dat een van de getoonde hoeken 125 waard is, het vinden van de metingen van de resterende 7 hoeken in de volgende figuur en de antwoorden rechtvaardigen.

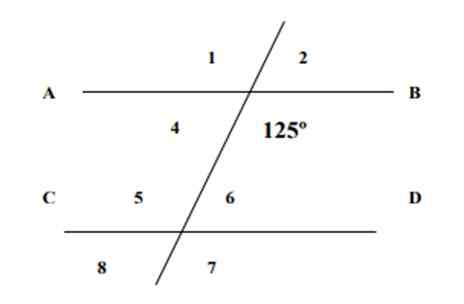Figuur 4. De lijnen en hoeken van oefening 1. Bron: f. Zapata.

Oplossing

Hoek 6 en hoek 125 zijn intern conjugaat, waarvan de som 180º waard is, volgens de eigenschap van de geconjugeerde hoeken, daarom:

∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º

Aan de andere kant zijn ∠6 en ∠8 tegenover de hoeken door het hoekpunt, waarvan de maatregel hetzelfde is. Daarom meet ∠8 55º.

Kan u van dienst zijn: vectoralgebra

De hoek ∠1 wordt ook tegen het hoekpunt tegen 125, dan kunnen we bevestigen dat ∠1 = 125º. We kunnen ook een beroep doen op het feit dat de overeenkomstige hoekenparen dezelfde maat hebben. In de figuur zijn deze hoeken:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125º

∠4 = ∠8 = 55 °

- Oefening 2

Zoek de waarde van X in de volgende figuur en de waarden van alle hoeken:

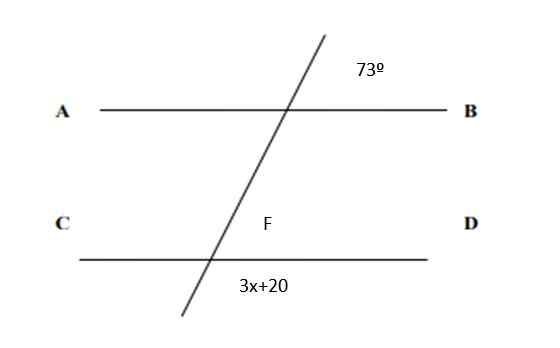Figuur 5. Lijnen en hoeken voor oefening 2. Bron: f. Zapata.

Oplossing

Omdat het overeenkomstige paren zijn, volgt hieruit dat F = 73º. En aan de andere kant is de som van de geconjugeerde paren daarom 180º:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Ten slotte is de waarde van X:

x = 87/3 = 29

Wat alle hoeken betreft, ze verschijnen in de volgende figuur vermeld:

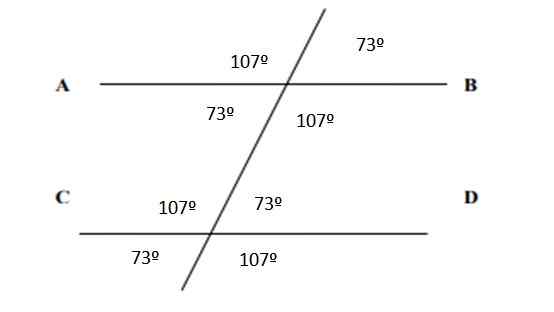Figuur 6. Hoeken die resulteren in oefening 2. Bron: f. Zapata.

Referenties

1. Hoekgroepen. Complementaire, aanvullende en explementaire hoeken verklaring. Hersteld van: thisiget.com/
2. Baldor, een. 1983. Flat and Space and Trigonometry Geometry. Culturele thuislandgroep.
3. Corral, m. Mathematics Libhethexts: hoeken. Hersteld van: wiskunde.Librhetxts.borg.
4. Mathmanie. Het classificeren en construeren van hoeken door hun meting. Hersteld van: Mathemania.com/
5. Wentworth, G. Planeetgeometrie. Hersteld van: Gutenberg.borg.
6. Wikipedia. Geconjugeerde hoeken. Hersteld van: is.Wikipedia.borg.