Schatting met intervallen

Wat is de schatting per intervallen?

De Schatting met intervallen Het is de manier om het bereik van waarden te bepalen waarin het bevolkingsgemiddelde kan worden opgenomen, gebaseerd op de informatie van een steekproef van eindige grootte, willekeurig geëxtraheerd uit de totale populatie.

Hij Schattingsinterval Het is lager omdat het monster groter is, maar het wordt breder als het niveau of percentage van de betrouwbaarheid van dezelfde toename.

Als u het bevolkingsgemiddelde van een bepaalde variabele in exacte vorm wilt weten, dan moet de totale bevolking worden overwogen, iets dat niet altijd haalbaar is, want als het een zeer grote populatie is, is het duur om de gegevens van de gegevens te krijgen volledige bevolking. Om deze reden worden een of meer willekeurige monsters van de totale populatie gebruikt om te nemen.

Het is gebaseerd op de hypothese dat, door een willekeurige steekproef te extraheren, niet bevooroordeeld en rekening houdend met evenredig alle lagen, dan moet de gemiddelde waarde van de steekproef zeer dicht bij die van het bevolkingsgemiddelde zijn.

De logica geeft aan dat hoe groter de steekproefgegevens, het verschil tussen de gemiddelde steekproefwaarde en de gemiddelde populatiewaarde lager is.

Schattingsinterval

In de praktijk, tenzij de volledige populatie bekend is, is het alleen mogelijk om met enige waarschijnlijkheid het interval te vinden waar het bevolkingsgemiddelde kan worden gevonden, gebaseerd op een steekproef van eindige grootte.

In het geval van een populatie die volgt op een normale verdeling, met Standaardafwijking σ , de Standaardverschil Tussen het bevolkingsgemiddelde μ en het gemiddelde monster van grootte N is gegeven door:

| μ - | ≤ σ / √n

Hier geeft het woord "standaard" aan dat 68% van de size monsters N, Ze hebben een gemiddelde waarde tussen het interval [μ - σ / √n, μ + σ / √n].

Kan u van dienst zijn: Divisibiliteit Criteria: wat zijn ze, wat zijn het nut en regels

Standaardraming

Een alternatieve interpretatie van het bovenstaande zou zijn om te zeggen dat het bevolkingsgemiddelde verkregen uit een steekproef van grootte N en de gemiddelde waarde wordt in het interval begrepen  [ - σ / √n, + σ / √n], Met 68% waarschijnlijkheid.

In de meeste echte gevallen is het niet mogelijk om de standaardpopulatie -afwijking te kennen, dus σ Het wordt benaderd door de standaardafwijking van het monster S, die als volgt wordt berekend:

S = √ (∑ (x_Je - ))² / √ (n-1).

Van daaruit krijgt u het interval dat het bevolkingsgemiddelde zou kunnen bevatten met een betrouwbaarheidsniveau van 68% (standaard betrouwbaarheidsniveau), gegeven door:

  -S / √n ≤ μ ≤ + s / √n

Dit populatiemeetinterval staat bekend als standaard schattingsinterval en werd alleen verkregen met de gegevens die beschikbaar zijn N.

Uit de vorige formule volgt hieruit dat, als u het schattingsinterval in tweeën wilde versterken, het noodzakelijk is verviervoudigen De grootte van het monster.

Schatting door betrouwbaarheidsintervallen

In bepaalde studies kan een standaardniveau van 68% onvoldoende zijn, dan is het noodzakelijk om de intervallen te bepalen met een willekeurig betrouwbaarheidsniveau γ.

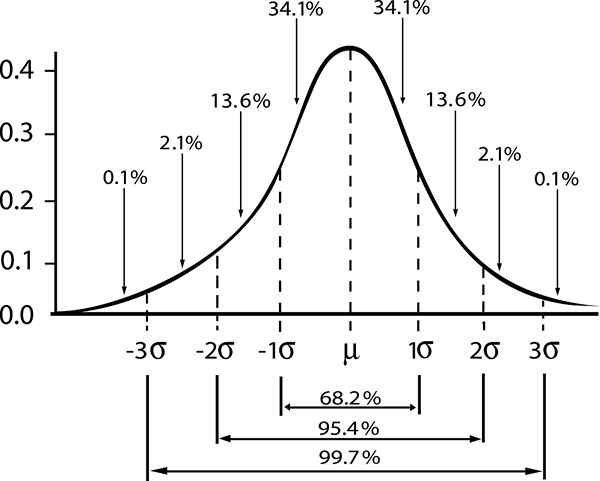
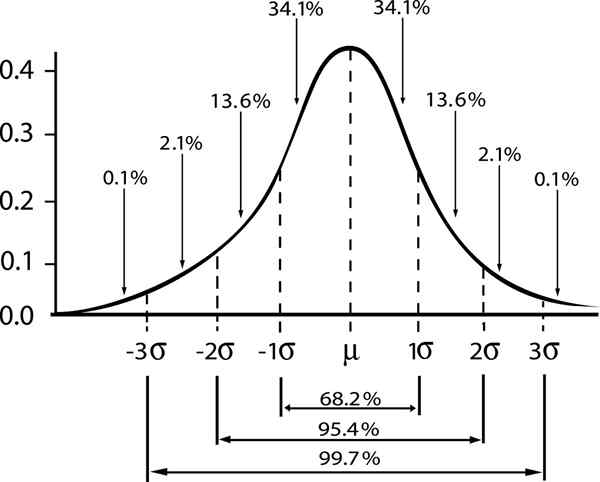De relatie tussen de betrouwbaarheidsmarge en het interval in een Gaussiaanse verdeling wordt getoond

Als we aan duiden door ε De standaardfout S/√n, Vervolgens de schattingfout voor een betrouwbaarheidsniveau γ zal worden gegeven door:

E = zy⋅ε.

Waar Zy Het is een getal waarmee de standaardfout wordt vermenigvuldigd en dus de foutmarge verkrijgt met een willekeurig betrouwbaarheidsniveau γ.

Om de factor te krijgen Zy, ga als volgt verder:

Het kan u van dienst zijn: rationele nummers: eigenschappen, voorbeelden en bewerkingen

Stap 1

Is de oproep significantieniveau α overeenkomend met het vertrouwensniveau γ door de volgende formule:

α = 1 - γ

Stap 2

De waarde wordt bepaald:

Dit is de opgebouwde frequentie in een normale verdeling getypeerd N (0,1) In het interval (-∞, Zy ].

Stap 3

Het wist Zy De vergelijking:

N (zy) = 1 - α/2

Omdat het een integrale vergelijking is, wordt deze klaring verkregen uit de normale distributietabellen, met behulp van de lineaire interpolatiemethode.

Stap 4

Als alternatief voor het gebruik van tabellen, zijn de statistische functies opgenomen in de spreadsheets zoals zoals Uitblinken, of Google -blad. Deze programma's bevatten een normale omgekeerde functie N^-1, zodat de correctiefactor Zy Het wordt verkregen direct evalueren van deze omgekeerde functie:

Zy = n^-1(1 - α/2).

Typische vertrouwensintervallen

De meest gebruikte betrouwbaarheidsniveaus zijn:

• Zy = 1; Standaard betrouwbaarheidsniveau γ = 0,68.
• Zy = 2; betrouwbaarheidsniveau γ = 0,95 (of significantieniveau 5%).
• Zy = 3; betrouwbaarheidsniveau γ = 0,997 (of 0,3%significantieniveau)

Voorbeelden

voorbeeld 1

Bepaal het gemiddelde gewichtsinterval van pasgeborenen gedurende de maand augustus in een grote stad op basis van een willekeurige steekproef van 100 baby's, waarbij een gemiddeld gewicht van 3100 gram werd verkregen met een monsterstandaardafwijking S = 1500 gram.

Oplossing

Ten eerste wordt de standaardfout van het monster bepaald:

ε = s/√n = (1500 g)/√100 = 150 g.

Daarom kan, beginnend bij dit monster, worden afgeleid dat het gemiddelde gewicht van baby's die in augustus in die stad zijn geboren tussen 2950 g en 3250 g ligt, met 68% waarschijnlijkheid.

Voorbeeld 2

Stel dat de grootte van de steekproef van baby's geboren in dezelfde maand augustus en in dezelfde stad van voorbeeld 1. Het gemiddelde monstergewicht is 3100 g met een standaard dispersie van 1500 g. 

Het kan u van dienst zijn: ontleding van natuurlijke getallen (voorbeelden en oefeningen)

Er wordt gevraagd om het gemiddelde gewichtsinterval van de pasgeborenen van die stad te schatten, van deze nieuwe steekproef.

Oplossing

Nu neemt de standaardfout af in factor 1/√2, Dus de nieuwe standaardfout van het gemiddelde gewicht zal 106 g zijn.

Vervolgens kan worden geschat, uit deze nieuwe steekproef dat het gemiddelde gewicht van pasgeborenen bestaat in het bereik van 2994 g tot 3206 g, met een waarschijnlijkheid van 68%.

Opdrachten

Oefening 1

Bepaal het gemiddelde gewichtsbereik van pasgeborenen in augustus, beginnend bij het monster gespecificeerd in Voorbeeld 1, met een waarschijnlijkheid van 95%.

Oplossing

Een betrouwbaarheidsniveau van 95% verdubbelt het gemiddelde gewichtsbereik, vergeleken met een betrouwbaarheidsniveau van 68%.

Daarom is het gemiddelde gewicht van pasgeborenen opgenomen in het bereik van 2800 gram bij 3400 gram met 95% zekerheid.

Oefening 2

Schat met een betrouwbaarheidsniveau van 99,7% het interval waarin het gemiddelde gewicht van pasgeborenen uit een grote stad zal worden gevonden, als een monster beschikbaar is met het gemiddelde gewicht van 100 baby's gelijk aan 3100 g, en met een standaardmonsterafwijking S = 1500 G.

Oplossing

De gemiddelde gewichtsfoutmarge, met 99,7% van de zekerheid, is drievoudig de gemiddelde fout, dat wil zeggen:

3*1500/√100.

Vervolgens wordt uit dit monster afgeleid dat het gemiddelde gewicht dat de pasgeborenen in het interval zullen worden opgenomen: 2650 gram tot 3550 gram, met een zekerheidsniveau van 99,7%. 

Uit dit resultaat wordt het waargenomen omdat een groter niveau van zekerheid de onzekerheid van het gemiddelde gewicht verhoogt tot een veel breder interval.