Kruisproduct

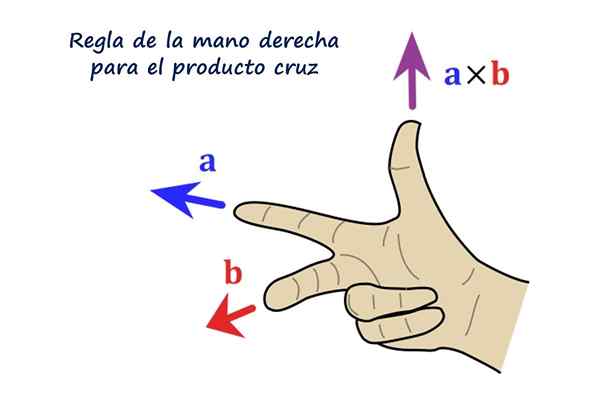
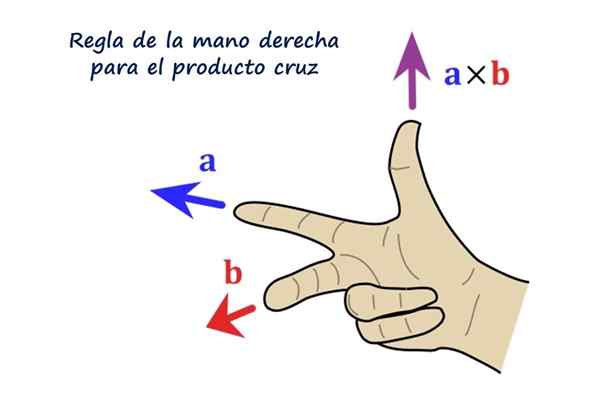Juiste regel voor het vectorproduct. Bron: f. Zapata.

Wat is het kruisproduct of vectorproduct?

Hij Kruisproduct, Ook wel vectorproduct genoemd, het is een type product dat wordt uitgevoerd tussen twee vectoren en resulteert in een andere vector, loodrecht op het vlak gedefinieerd door de eerste twee.

Het kruisproduct tussen twee vectoren naar En B, Het resulteert in een andere vector R, Wiskundig wordt als volgt geschreven:

naar × B = R

Het leest zo: “A cruz b gelijk aan r ".

In gedrukte tekst worden vectoren geschreven met gewaagde teksten, of met een pijl op de letter, om ze te onderscheiden van hun grootte of module. Hiervoor worden ze gebruikt, uitwisselbaar, modulebars en huidige letters, dus de absolute waarde van de vector naar Symbool is als volgt geschreven:

│naar│ = A

De absolute waarde of module van het vectorproduct tussen twee vectoren wordt berekend door de module van beide vectoren te vermenigvuldigen met de hoek θ tussen hen:

R = a ∙ b ∙ sen θ

De richting van de vector R Het staat loodrecht op die van vectoren naar En B. Het gevoel van R Het is dextrogyr van naar in de richting van B En in de praktijk wordt het bepaald met behulp van de regel van de rechterhand, die bestaat uit het als volgt van de index, medium en duim van de rechterhand:

• De wijsvinger wordt geplaatst volgens de vector naar
• Met de middelvinger volgt de vector B
• De duim, uitgebreid, geeft de richting en richting van de vector aan R.

Deze bestelling moet exact worden gevolgd, omdat het vectorproduct niet commutatief is, dat wil zeggen naar × B ≠ B × naar En als de vectoren worden uitgewisseld, wordt het juiste resultaat niet verkregen.

Kan u van dienst zijn: bestaan ​​en uniekheid Stelling: demonstratie, voorbeelden en oefeningen

De lezer wordt geadviseerd om zijn rechterhand te plaatsen zoals de figuur laat zien, de index die naar links wijst, vertegenwoordigt de vector naar, De middelvinger volgt B En het wijst rechtstreeks naar de lezer, ten slotte geeft de duim aan, wijzend naar richting en richting van de vector naar × B = R.

Cruz Product Properties

-Het kruis- of vectorproduct tussen twee vectoren resulteert altijd in een andere vector.

-Een kruisproduct is daarom niet commutatief: naar × B ≠ B × naar.

-Voor het kruisproduct is het waar dat: naar × B = - (B × naar)). Deze eigenschap wordt gebeld anti-eigenwijsheid.

-De resulterende vector van het vectorproduct tussen twee vectoren is loodrecht (normaal) voor genoemde vectoren.

-Uit het bovenstaande volgt dat het vectorproduct tussen vectoren met dezelfde richting nul is. In het bijzonder naar × A = 0.

-Het kruisproduct voldoet aan de distributiewetgeving met betrekking tot de som: naar × (B+C) = naar × B + naar × C

-Als M een scalair is, dan m (naar × B) = m naar × B = naar × m B

Kruis product tussen eenheidsvectoren

De drie eenheidsvectoren, geroepen Je, J En k, Ze staan ​​loodrecht op elkaar en geven de drie opmerkelijke richtingen van de ruimte aan: hoge, brede en diepte. Deze adressen staan ​​loodrecht op elkaar.

Het vectorproduct tussen de eenheidsvectoren wordt gemakkelijk bepaald door de rechterhandregel en rekening houdend met de eigenschappen van het kruisproduct:

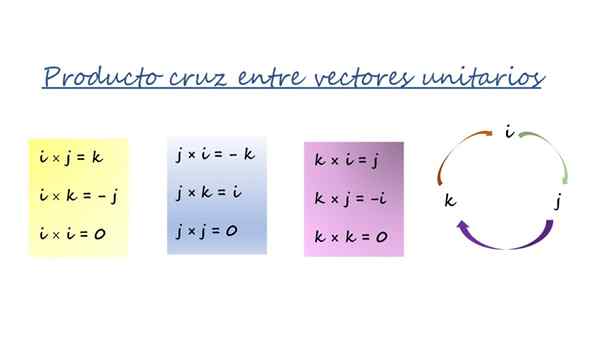Vectorproduct van Cartesiaanse eenheidsvectoren. Bron: f. Zapata.

De drie gekleurde dozen in de figuur zijn samengevat in de ronde met pijlen naar rechts en worden op deze manier gebruikt:

-Bij het vermenigvuldigen in de richting van de pijl is het resultaat de vector voor de pijl en heeft het een positief teken. Bijvoorbeeld door vectorly te vermenigvuldigen J En k, De derde vector is Je, En aangezien de volgorde de betekenis van de pijl volgt, is het bord +.

Kan u van dienst zijn: vectorfuncties

-En als het zich in de tegenovergestelde richting vermenigvuldigt met de pijl, is het resultaat de derde vector voor de pijl, maar met een negatief teken.

De eenheidsvectoren vormen een basis, dus elke andere vector kan in termen van hen worden geschreven. Dit vergemakkelijkt de berekening van het kruisproduct sterk tussen twee willekeurige vectoren in de ruimte.

Hoe het kruisproduct van twee vectoren analyseren analytisch

Wanneer vectoren naar En B Ze hebben een willekeurige richting in de ruimte, met componenten langs elk van hen, het is gemakkelijker om het kruisproduct op een analytische manier te berekenen en ze uit te drukken in termen van de eenheidsvectoren Je, J En k:

• naar = a_X Je + naar_En J + naar_Z k
• B = B_X Je + B_En J + B_Z k

Nu wordt de distributieve eigenschap van vermenigvuldiging gebruikt, die ook geldig is voor het kruisproduct:

naar × B = (a_X Je + naar_En J + naar_Z k) × (B_X Je + B_En J + B_Z k) =

= (a_X Je × B_X Je) + (A_X Je × B_En J) + (A_X Je × B_Z k) + (A_EN J × B_X Je) + (A_EN J × B_En J) + (A_EN J × B_Z k) + (A_Z k × B_X Je) + (A_Z k × B_En J) + (A_Z k × B_Z k))

Kruisproducten tussen gelijke eenheidsvectoren worden geannuleerd, omdat ze parallelle vectoren zijn, wat deze expressie tot 6 termen vermindert:

naar × B = (a_X Je × B_En J) + (A_X Je × B_Z k) + (A_EN J × B_X Je) + (A_EN J × B_Z k) + (A_Z k × B_X Je) + (A_Z k × B_En J))

Ten slotte resulteert elk product met de bovenstaande figuur in:

naar × B = a_X B_En k + naar_X B_Z ( -J) + a_EN B_X ( -k) + a_EN B_Z Je + naar_Z B_XJ + naar_Z B_En ( -Je) =

= (a_EN B_Z - A_Z B_En)) Je + (naar_Z B_X - A_X B_Z)) J + (naar_X B_En - A_EN B_X)) k

Cruz -product via een determinant

Het is niet nodig om de bovenstaande formule te onthouden, maar de ronde van de voorgaande figuur gemakkelijk toe te passen of eenvoudig de onderstaande determinant uit te voeren, wat volledig equivalent is:

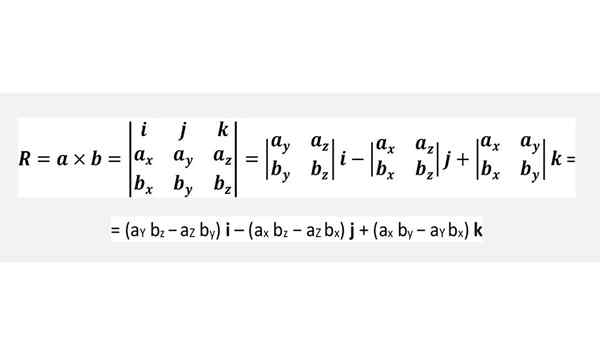
Voorbeeld

Uitgaande van vectoren naar En B Zijn:

• naar = 5 Je - J + 4 k
• B = -Je + 0J +7 k

Het kruisproduct tussen hen wordt berekend door de respectieve coördinaten te identificeren en te vervangen:

Kan u van dienst zijn: Hyperbolische paraboloïde: definitie, eigenschappen en voorbeelden

naar_X = 5; naar_En = −1; naar_Z = 4; B_X = −1; B_En = 0: B_Z = 7

naar × B = [(−1) ∙ 7 - 4 ∙ 0] Je + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] Je + [(−4 - 35) J + [0 - 1] k =

= (−7) Je - 39 J - k

De determinante methode biedt hetzelfde resultaat.

Oefening

Bereken door determinanten, het kruisproduct onder de vectoren:

• of = 2 Je +J + 5 k
• v = Je + 4J +7 k

En bepaal het gebied van het parallellogram dat wordt ingediend door de vorige vectoren, zoals weergegeven in de figuur:

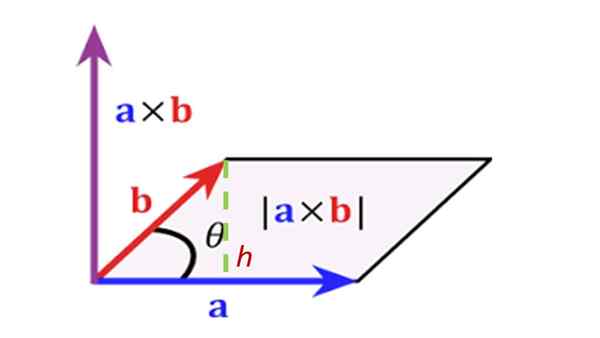
Oplossing

Waarden van vectorencoördinaten worden vervangen in de determinant:

Het vastberaden parallellogramgebied is de module van het vectorproduct ertussen, resulterend: r = 17.3 gebiedseenheden.