In afwachting van een lijnformule en vergelijkingen, representatie, voorbeelden

De hangende lijn Het is de raaklijn van de hoek θ dat deze lijn vormt met de horizontale as, die volgens de conventie in de tegenovergestelde richting van de klokken wordt gemeten. De helling van elke lijn is altijd constant en daarom is het een van de meest essentiële kenmerken.

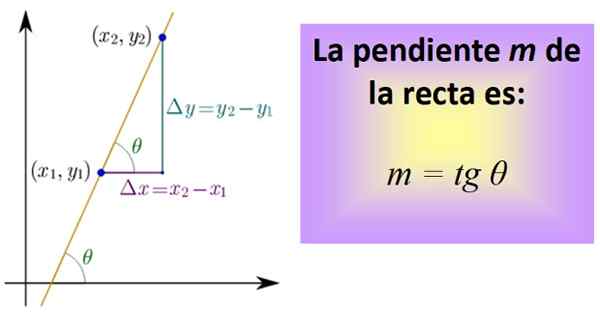
Om het te berekenen, moet u twee punten van de lijn kennen, waarvan de coördinaten zijn (x x₁,En₁) en (x₂,En₂)). Tussen beide punten wordt een segment getekend dat tot de lijn behoort en vervolgens worden de segmenten die de afstand tussen X vertegenwoordigen getekend₁ en x₂, en tussen en₁ en en₂, zoals in de onderste figuur.

Figuur 1. De helling van een lijn is de raaklijn van hoek θ. Bron: Wikimedia Commons.

De drie segmenten vormen een juiste driehoek waarvan de benen zijn: Δx = x₂ - X₁  en Δy = en₂ - En₁. Ze komen respectievelijk overeen met een horizontale verplaatsing en een andere verticaal.

Nu wordt een quotiënt gedefinieerd, genaamd tangent van de hoek θ en afgekort Tg θ, wat precies de helling is M van de lijn:

m = tg θ = Δy / Δx

Merk op dat voor een lijn deze hoek constant blijft, ongeacht de punten die zijn genomen om de raaklijn te berekenen. In elk geval biedt deze waarde ons een maat voor hoe geneigd het de lijn is.

Door de coördinaten van de geselecteerde punten blijft de hellingsformule:

M = (y - y₁ ) / (X₂ - X₁))

[TOC]

Grafische weergave

Hieronder hebben we verschillende situaties waarin het concept van helling relevant is. De waarde ervan kan gemakkelijk worden berekend door de respectieve verticale en horizontale verplaatsing te meten en vervolgens het quotiënt in het begin aangegeven te maken.

Dit geeft ons een idee van de helling of de achteruitgang van een structuur, zoals een helling, een dak of een weg:

Kan u van dienst zijn: willekeurige bemonstering: methodologie, voor-, nadelen, voorbeelden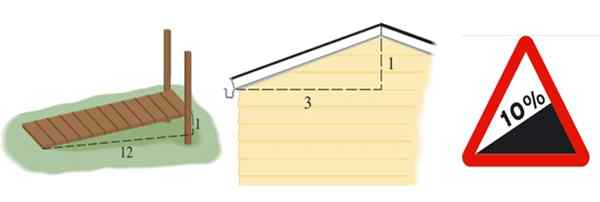 Figuur 2. Van links naar rechts de helling van een helling, een dak en de helling van een weg, de laatste uitgedrukt in percentage. Bron: Stewart, J. Precáculculo en Wikimedia Commons (rechter beeld).

De helling van de helling in figuur 2 aan de linkerkant is m = 1/12, het dak is m = 1/3 en de weg wordt uitgedrukt in percentage. Een percentage van 10 % betekent dat voor elke 100 meter dat horizontaal vooruit gaat, ze 10 meter hoog verdienen:

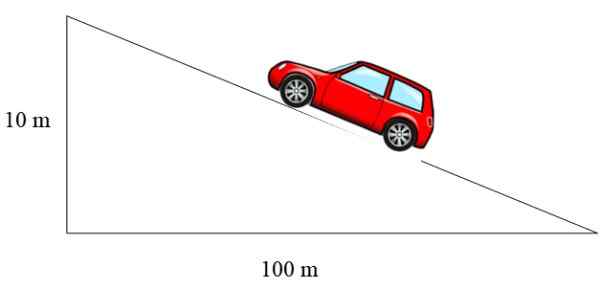figuur 3. Een voertuig stijgt door een helling waarvan de helling 10% is. Bron: f. Zapata.

In dit geval is de helling 10/100 = 0.1, dat als percentage wordt uitgedrukt, is gelijk aan 10%.

Soorten helling

De helling van een lijn kan positief, negatief of nul zijn. De in figuur 1 getoonde lijn heeft bijvoorbeeld een positieve helling. We waarderen het meteen omdat we zien dat de lijn is "opgeheven" als we hem van links naar rechts zien.

Als de lijn afdaalt om het van links naar rechts te zien, dan is de helling negatief. En wanneer een lijn horizontaal is, is de helling niet nul.

Ten slotte is de helling voor verticale lijnen niet gedefinieerd.

De grafische weergave van elk type is hieronder te vinden:

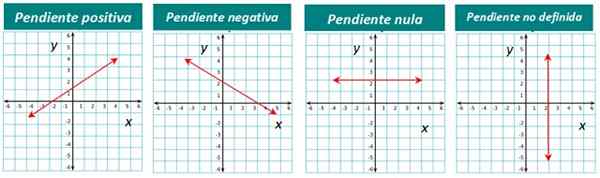Figuur 4. De lijnen volgens je helling. Bron: f. Zapata.

Hoe wordt de helling een lijn berekend??

Het berekenen van de helling is heel eenvoudig, u hoeft alleen maar verticale verplaatsing en horizontale verplaatsing te vinden en vervolgens het quotiënt tussen de twee te maken.

Wanneer u de tekening van de lijn in het Cartesiaanse vlak hebt, kiezen deze verplaatsingen twee punten van de lijn P₁ En P₂, Het bepalen van hun coördinaten en het toepassen van de definitie die in het begin wordt gegeven:

Kan u van dienst zijn: wat vertegenwoordigt de lengte van de verplaatsing van de zeshoek

M = (y - y₁ ) / (X₂ - X₁ ))

Omdat de waarde van de helling onafhankelijk is van de keuze van P₁ En P₂ , We gaan een punt P kiezen van coördinaten (x, y) die tot de lijn behoort, waarvan de coördinaten niet bekend zijn, en een ander punt p₁ wiens coördinaten zijn: (x₁,En₁)).

De helling is:

M = (y - y₁) / (x - x₁))

We kunnen de En:

en en₁ = m (x - x₁))

Stel nu het punt P₁ Het is de kruising van de lijn met de verticale as, van coördinaten (0, b). Dit vervangen in de vorige vergelijking:

en - b = m (x - 0) → y = mx + b

Deze uitdrukking staat bekend als de vergelijking van de lijn in de vorm In behandeling - kruising, Omdat de lijn ondubbelzinnig is bepaald wanneer de helling en kruising met de verticale as bekend zijn.

Alleen de helling kennen is niet voldoende om een ​​lijn in het vlak te karakteriseren, omdat oneindig rechte kan dezelfde helling hebben, wat betekent dat ze parallel zijn, maar door andere punten gaan.

Opgeloste oefeningen

- Oefening 1

Zoek de helling van de lijn die wordt getoond in de volgende figuur:

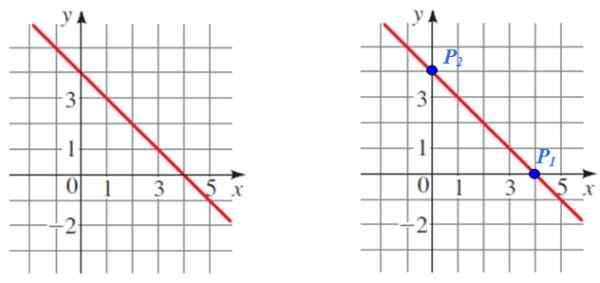Figuur 5. Door de grafiek van een lijn worden twee punten gekozen om de helling te berekenen. Bron: f. Zapata.

Oplossing

P₁ En P₂ Het zijn twee eenvoudige -tot -gelezen punten die zullen dienen voor de berekening, merkt ook op dat zij de respectieve kruispunten zijn met de coördinaatassen.

De coördinaten van elk punt zijn:

P₁ (4.0) en P₂ (0,4)

Door de hellingsvergelijking te vervangen:

m = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

De helling is negatief, wat werd verwacht na het observeren van de afbeeldingen.

Kan u van dienst zijn: complexe nummers: eigenschappen, voorbeelden, bewerkingen

- Oefening 2

Zoek de vergelijking van de lijn die door het punt gaat (1, -6) en parallel is aan de lijn y = 2x - 3.

Oplossing

De helling van de gezochte lijn moet dezelfde zijn als die van y = 2x - 3, omdat ze parallel zijn. Voor deze lijn is de helling m = 2, daarom heeft degene die we zoeken de vorm:

en en₁ = 2 (x - x₁))

Nu vervangen we het punt waardoor onze lijn voorbijgaat: x₁ = 1 en₁ = -6.

en - (-6) = 2 (x - 1)

Daarom y = 2x - 2 - 6 → y = 2x - 8

Voorbeelden

Twee hoeveelheden kunnen zodanig gerelateerd zijn dat uw grafiek een rechte lijn is. In dat geval wordt gezegd dat de hoeveelheden lineaire afhankelijkheid hebben en de helling van de lijn kan worden geïnterpreteerd als de reden voor de verandering van de ene variabele in de andere.

voorbeeld 1

Stel dat een zwembad gevuld is met water tot een tarief constant in de tijd. Natuurlijk, hoe meer tijd verstrijkt, hoe meer water het wordt opgeslagen. Welnu, de snelheid waartegen het zwembad is gevuld, is precies de helling van de lijn die het volume tot tijd relateert:

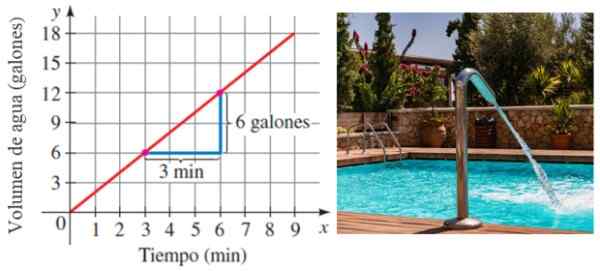Figuur 6. De helling als reden voor verandering. Bron: Stewart, J./Pxfuel.

In dit voorbeeld wordt het zwembad gevuld met een snelheid van 6/3 gallons per minuut of 2 gallons/minuut.

Voorbeeld 2

Wanneer een mobiel in een rechte lijn met constante snelheid beweegt, is de helling van de positiegrafiek afhankelijk van de tijd, is niemand minder dan die snelheid. De grafiek toont een mobiel met positieve snelheid, wat betekent dat deze weggaat van de oorsprong.

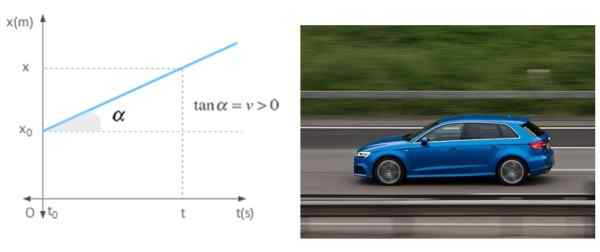Figuur 7. De helling van de versus tijdgrafiek is de snelheid van de mobiel in een uniforme rechtlijnige beweging. Bron: Wikimedia Commons/Pixabay.

Referenties

1. Alvarez, J. De helling van een weg. Hersteld van: Geogebra.is.
2. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
3. Hoffman, J. Selectie van wiskundeproblemen. Deel 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
6. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.