Notatie ontwikkeld wat is, voorbeelden en oefeningen

De ontwikkelde notatie Het is er een waarin een numerieke figuur wordt uitgedrukt als een som waarin de positionele waarde van elk cijfer dat het nummer vormt, in aanmerking wordt genomen.

Bijvoorbeeld wanneer het schrijven van een figuur als 2345 elk cijfer ervan een positionele hiërarchie heeft. Het lezen van het rechter extreme cijfer links, de hiërarchie of waarde groeit.

Figuur 1. Met negen grafemen is het mogelijk om elk figuur weer te geven.

In figuur 2345 vertegenwoordigt cijfer 5 vijf eenheden, cijfer 4 vertegenwoordigt vier tientallen, de 3 komt overeen met de derde positie van links naar rechts en daarom vertegenwoordigt de 3 drie honderden, uiteindelijk vertegenwoordigt de 2 tweeduizend. Dat is, in ontwikkelde of uitgebreide notatie, de figuur 2345 is geschreven:

2345 = 2 duizend + 3 honderd + 4 tientallen + 5 eenheden

Maar het kan ook als volgt worden uitgedrukt:

2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.

De figuur 2345 kan ook worden geschreven als de som van de bevoegdheden van 10:

2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0

Waar de circumflejo ^ betekent dat de aangegeven exponent wordt verhoogd. Bijvoorbeeld 10^3 = 10 x 10 x 10 = 1000. Een andere manier om de exponenten te schrijven is door een toezicht:

2345 = 2 x 10³ + 3 x 10² + 4 x 10¹ + 5 x 10⁰

[TOC]

Positioneel nummeringssysteem

Het Arabische nummers -systeem zijn de cijfers die dagelijks worden gebruikt in de overgrote meerderheid van continenten en landen in de wereld. Arabische nummers zijn een basissysteem 10 omdat tien symbolen of grafemen worden gebruikt om elk nummer te schrijven. Deze tien symbolen zijn:

0 1 2 3 4 5 6 7 8 9

Met slechts één van deze symbolen kunnen figuren tussen nul tot negen worden uitgedrukt. Om cijfers groter dan negen uit te drukken, het positionele systeem op basis van tien. Figuur 10 is een dozijn en nul -eenheden. Figuur 11 is een dozijn en een eenheid. Afbeelding 123 (honderd twintig drie) is honderd, twee tientallen en drie eenheden. Geschreven in de vorm van machten van tien zal het nummer 123 zijn:

Kan u van dienst zijn: 60 delers

1 × 10^2 + 2 × 10^1 + 3 × 10^0

Waar:

10^2 = 10 x 10 = 100

10^1 = 10

10^0 = 1.

Met dit voorbeeld is het duidelijk dat de positie van het cijfer aan het uiteinde positie 0 is en het aantal eenheden vertegenwoordigt, dat van het tweede cijfer van rechts naar links is positie 1 en het aantal tientallen vertegenwoordigt, het derde cijfer (rechts naar links) heeft positie 2 en vertegenwoordigt de honderden.

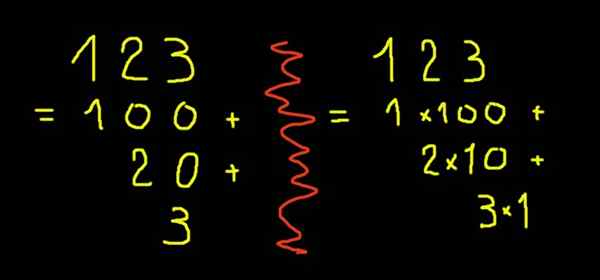Figuur 2. Ontwikkelde notatie van figuur 123.

Fractionele of decimale getallen

Met het decimale positionele systeem is het ook mogelijk.

Om de fractie ½ in het Arabische decimale systeem weer te geven, dat wil zeggen, de helft van de eenheid is geschreven:

½ = 0,5

Om deze uitdrukking in ons systeem te bereiken op basis van 10, zijn de volgende bewerkingen gemaakt:

1- Vervorming van teller en noemer voor 5 om de equivalente fractie 5/10 = 1/2 te hebben. 

2- Divide met 10 is equivalent aan het vermenigvuldigen met het vermogen op basis van tien met exponent minder één (10^-1), dat is 5/10 = 5 × 10^-1.

3- De negatieve exponent geeft aan hoe vaak het cijfer wordt aangegeven vanuit de positie van de eenheid wordt uitgevoerd of gepositioneerd, in ons geval zou het 0,5 zijn.

4- ½ = 0,5 in uitgebreide notatie is het als volgt geschreven:

0.5 = 0x10^0 + 5 × 10^-1

Waarbij 10^-1 = 0,1 een tiende is (de fractie die overeenkomt met de eenheid verdeeld in 10 gelijke delen).

Op deze manier komt het nummer 0,5 overeen met vijf tienden, maar het nummer 0,05 komt overeen met 5honderdste en 0,005 tot 5 duizendste.

Kan u van dienst zijn: waarom is algebra belangrijk in bepaalde situaties in het dagelijkse leven?

Ontwikkelde notatie voorbeelden 

voorbeeld 1

Gezien het 40201 -cijfer in standaardnotatie, converteer het naar de ontwikkelde notatie.

Oplossing: 

4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201

Voorbeeld 2

Schrijf de fractie ¾ in uitgebreide notatie.

Oplossing: 

In dit geval zijn er driekwart van de eenheid. 

3/4 = 15/20 = 75/100 = 0.75 = 7/10 + 5/100 = 

7 × 10^-1 + 5 × 10^-2.

Zei in woorden zou zo zijn:

De fractie ¾ komt overeen met zeven tienden plus vijfhonderdste.

Ontwikkelde notatieoefeningen

Oefening 1

Zeg in woorden de uitdrukking ontwikkeld van de 40201 figuur van voorbeeld 1.

Oplossing:

De ontwikkelde notatie is als volgt:

40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 

Dat in woordtaal wordt gezegd:

Vier tienduizenden, plus duizenden duizenden, plus tweehonderd, meer nul tientallen, plus een eenheid.

Oefening 2

Druk in de woorden uit de vorige figuur en splitsen de bijbehorende uitdrukking op.

Oplossing:

De 40201 -figuur in woorden wordt als volgt uitgedrukt:

Veertigduizend tweehonderd één

De vorige zin kan zich ontwikkelen als:

40 × 1000 + 2 × 100 + 1

Men kan zeggen dat de manier om de cijfers uit te spreken, een halfontwikkelde manier is om het uit te drukken.

Oefening 3

Schrijf het nummer 7/3 ontwikkelde manier.

Oplossing:

Het is een figuur uitgedrukt als een ongepaste fractie, omdat de teller groter is dan de noemer, is de figuur groter dan de eenheid.

Deze ongepaste fractie kan worden afgebroken als de som van breuken 6/3 + 1/3. De eerste van de breuken resulteert in een geheel getal 2, terwijl 1/3 = 0.333333, waarbij cijfer 3 voor onbepaalde tijd wordt herhaald. Zodat de decimale expressie die is ontwikkeld van de 7/3 figuur altijd een benadering zal zijn:

Kan u van dienst zijn: vierhoekig: elementen, eigenschappen, classificatie, voorbeelden

7/3 = 2 + 1/3 ≃ 2 + 0.333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.

Oefening 6

Schrijf in standaardnotatie en ontwikkelde vervolgens het nummer: Twintig -drie miljard tweehonderdvijftig miljoen vijfhonderd twintig -zes duizenden driehonderd twintig -vijf met drie twintig -drieduizendste.

Oplossing:

Er moet aan worden herinnerd dat a Millardo is het equivalent van één miljard. Het woord Millardo Het werd aanvaard door de Royal Spaanse Academie in 1995 op verzoek van de overleden Venezolaanse president Rafael Caldera, een lid van de Venezolaanse Academie van Language. In dat geval wordt de figuur van de standaardnotatie als volgt geschreven:

23.2501526.325,023

23 miljard + 250 miljoen + 526 duizend + 325 eenheden + 23 duizendste. 

23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3

Ten slotte is de figuur in ontwikkelde notatie geschreven:

2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.

Referenties

1. Khan Academy. Positionele waardetabellen. Hersteld van: is.Khanacademy.borg
2. Khan Academy. Schrijf een ontwikkeld nummer (video). Hersteld van: is.Khanacademy.borg
3. Ifrah, Geoges (1998): Universal History of Figures. Espasa calpe s.NAAR.
4. Wikipedia. Positionele notatie. Hersteld van: is.Wikipedia.com
5. Wikipedia. Millardo. Hersteld van: is.Wikipedia.com