Decimale notatie
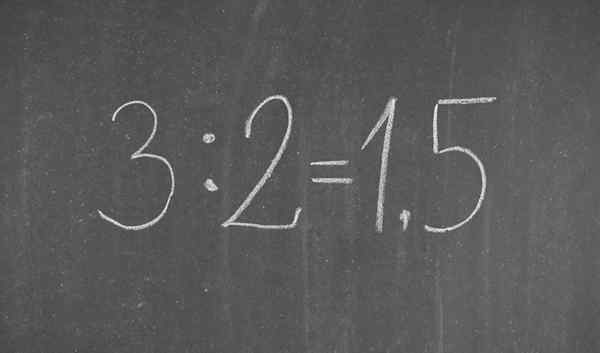
- 4439
- 1232
- Pete Heaney V
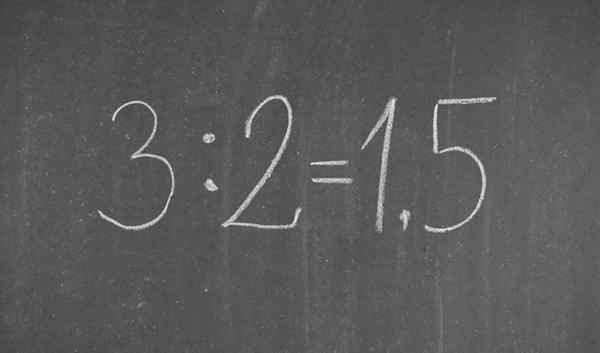 De 3/2 fractie geschreven in decimale notatie
De 3/2 fractie geschreven in decimale notatie Wat is decimale notatie?
De decimale notatie Het bestaat uit het schrijven van een reëel getal door een volledig deel en een decimaal deel, beide gescheiden door een punt of een komma. Het hele deel is achtergelaten en het decimale deel rechts van dat punt.
De 0 kan zowel in het hele deel als in het decimaal verschijnen. De volgende cijfers zijn bijvoorbeeld decimale getallen:
- 0.25
- 1.5903
- 4.19367
Merk op dat het decimale deel van deze getallen eindig is, maar er zijn ook getallen met een oneindig decimaal gedeelte, zoals 0,33333 ..., waar suspensieve punten worden geplaatst als een manier om aan te geven dat het aantal decimalen voor onbepaalde tijd doorgaat.
Over het algemeen kan een eindig decimaal nummer worden geschreven als:
N.naar1naar2naar3… naarN
Als een geheel getal en n de hoeveelheid decimalen, terwijl een oneindig decimaal de vorm aanneemt:
N.naar1naar2naar3..
In het decimaal 0.25 worden geïdentificeerd:
- N = 0
- naar1 = 2
- naar2 = 5
Decimalen ontstaan als een andere manier om rationele getallen uit te drukken, die zijn gevormd of gebroken. In feite kan elke fractie in decimale notatie worden geschreven, zoals onmiddellijk zal worden gezien.
Ze dienen ook om getallen weer te geven die niet afkomstig zijn van een breuk, de zo -gevallen irrationele nummers, zoals: π, √2, √3, √5, het nummer "e" en vele andere.
Voorbeelden van decimale getallen
Een decimaal getal kan op een zeer eenvoudige manier worden verkregen uit een fractie: het quotiënt van de teller tussen de noemer berekenen. Als de noemer de eenheid is, gevolgd door nullen, is dit heel eenvoudig:
- 8/10 = 0.8
- - (5/100) = −0.05
In het eerste geval, aangezien de noemer 10 is, wordt het decimale punt onmiddellijk links van de 8 en het decimaal 0 geplaatst.8 leest "8 tienden" of "Zero Point Eight".
In het tweede geval, aangezien de noemer 100 is, moet u het decimale punt twee plaatsen links van 5 plaatsen, en omdat het aantal negatief is, leest het "minder 5honderdsten" of "minder nul nul punt vijf".
Wanneer de noemer niet de eenheid is, gevolgd door 0, wordt de lange divisie gebruikt:

Merk op dat om deze divisie uit te voeren, omdat de teller minder is dan de noemer, deze eerst met 10 werd vermenigvuldigd en daarmee een 0 werd gevolgd door het decimale punt in het quotiënt, om de bewerking niet te wijzigen, zo niet Om de bewerking te wijzigen. Ga dan normaal verder om 10 door 2 te verdelen, wat gelijk is aan 5 en het divisieresidu is 0.
Kan u van dienst zijn: vectorbedragenDe decimale vorm van fractie ½ is 0.5, dat "Zero Point Five" wordt gelezen:
Fractie 7/8 is een ander voorbeeld. Aangezien 7 minder dan 8 is, vermenigvuldigt het 7 × 10 = 70, een 0 wordt in het quotiënt geplaatst gevolgd door het decimale punt en is normaal verdeeld:
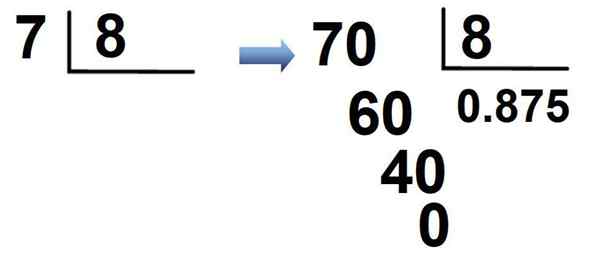
Het resultaat is dat de fractie in decimale notatie wordt geschreven als:
7/8 = 0.875
Dit aantal is, net als het vorige resultaat, een eindig decimaal en een manier om het te lezen is: "Zero Point Achthonderdhonderdveventig -vijf". Via deze procedure worden de volgende breuken ook geschreven in decimale notatie:
8/10 = 0.8
5/7 = 0.714285714…
9/20 = 0.Vier vijf
3/8 = 0.375
Merk op dat zoals in al deze breuken de teller minder is dan de noemer, het gehele deel van de resulterende decimalen 0 is. Een gemengd aantal of een Ongepaste breuk (Dat wiens teller groter is dan zijn noemer) heeft ook een decimale weergave.
In dit geval is het hele deel groter dan of gelijk aan 1 als de fractie positief is en minder dan -1 als deze negatief is:
9/4 = 2.25
10/3 = 3.333333…
−12/5 = −2.4
1 ½ = 1.5
2 ¾ = 2.75
Hele deel en fractioneel deel van de negatieve decimalen
In de vorige voorbeelden werd waargenomen dat om de decimale expressie van een fractie te vinden, een teller en noemer gewoon verdeeld zijn. Zelfs als de fractie negatief is, wordt eenvoudig het min -teken op de equivalente decimient expressie geplaatst.
Het hele deel en het fractionele deel van een decimaal verschillen echter volgens het teken dat u draagt.
Wanneer een decimaal positief is, zoals 2.25, het hele deel is 2 en het decimale deel is 0.25 En het nummer kan worden geschreven als de som van het gehele deel en het decimale gedeelte, zoals deze:
2.25 = 2 + 0.25
Het gehele deel wordt gedefinieerd als het gehele getal dat direct lager is dan het decimaal en het decimale deel is altijd positief. Voor 2.25, het onmiddellijk lagere gehele getal is 2.
Maar in het geval van fractie −12/5, gelijkwaardig aan de decimaal −2.4 Het bovenstaande werkt niet.
Kan u van dienst zijn: wat zijn de delen van het Cartesiaanse vlak?)
−2 + 0.4 = −1.6 ≠ −2.4
Daarom het hele deel van −2.4 kan niet −2 zijn, maar het onmiddellijk lagere geheel getal: −3. Maar in dat geval zou het fractionele deel niet 0 zijn.4, sinds door toe te voegen:
−3 + 0.4 = −2.6 ≠ −2.4
Dus wat is het decimale deel van het negatieve getal −2.4? Het trekt het decimale nummer af van het gehele deel en het resultaat zal altijd positief zijn:
−2.4 - ( - 3) = 0.6
Ten slotte is bewezen dat door het toevoegen van het hele deel en het fractionele gedeelte, het gezochte decimaal wordt verkregen:
−3 + 0.6 = −2.4
De procedure om een heel deel en een decimaal onderdeel van elk getal te vinden, ongeacht het teken, is op deze manier samengevat:
- Het gehele deel is het geheel getal dat direct lager is dan het decimale nummer.
- Het decimale gedeelte wordt berekend door het decimaal af te trekken van zijn gehele deel.
Voor praktische berekeningsdoeleinden is het decimale nummer −2 echter.4 kan worden afgebroken als - (2 + 0.4) = - 24/10 of:
)
Soorten decimalen
Er zijn decimale getallen waarvan het decimale gedeelte eindig of oneindig is, dat wordt gebruikt als een classificatiecriteria:
Eindige of exacte decimalen
Wanneer de decimalen eindig zijn, zoals 0.125, er wordt ook gezegd dat ze dat zijn exacte decimalen.
Oneindige decimalen
Een oneindig decimaal wordt verkregen wanneer het residu van de verdeling tussen teller en noemer nooit wordt gemaakt 0.
Op voorwaarde dat het decimaal afkomstig is van het quotiënt tussen twee gehele getallen, is dit decimale deel periodiek, dat wil zeggen dat het bestaat uit een of meerdere figuren die voor onbepaalde tijd worden herhaald, genoemd, genoemd, periode.
Bijvoorbeeld nummer 3.333333 ... afkomstig van de ongepaste fractie 10/3, het is een periodiek decimaal: het hele deel is 3 en na het decimale punt wordt nummer 3 voor onbepaalde tijd herhaald. Dit kan worden gesymboliseerd door een curve of hoed te plaatsen op het getal dat wordt herhaald:



Ten slotte zijn er oneindige decimalen die geen kranten zijn, die niet afkomstig zijn van het quotiënt tussen twee hele getallen. Zoals in het begin vermeld, behoren deze decimalen tot het geheel irrationele nummers, Zoals het PI -nummer bijvoorbeeld.
Opgeloste oefeningen
Oefening 1
Schrijf numeriek de volgende decimale nummers:
a) nul punt vierhonderd veertig -seven
b) Vijfduizendste
C) twee eenheden en vijfhonderdste
d) Drie punt twintig -seven negatief
e) Eén punt achthonderd twintigduizend vijfhonderd zestigzestig
-
Oplossing
A) 0.447
B) 0.005
C) 2.05
d) −3.27
e) 1.824563
Oefening 2
Classificeer de volgende decimale getallen in exacte decimale, pure kranten, gemengde kranten of irrationele cijfers. Geef in alle gevallen de waarde van het gehele deel aan, en als het kranten of gemengde kranten zijn, geven ook de waarde van de periode en de voorste, indien van toepassing:
A) 0.35627
b) 1.21212121…
c) −1.32
d) 1.414213562… = √2
-
Oplossing
a) 35627 is een exacte decimaal. Het hele deel is 0 en het decimale gedeelte is 0.35627.
b) 1.21212121 ... is een oneindige decimaal en pure krant, het hele deel is 1 en de periode is 21.
c) −1.32 is een exacte en negatieve decimaal, waarvan het hele deel −2 is. Het decimale gedeelte wordt berekend door het decimale nummer van het gehele deel af te trekken:
−1.32 - (−2) = 0.68
D) De decimale expressie van √2 is oneindig en niet periodiek, omdat het een irrationeel aantal is.
Het is een gemengde krant, het hele deel is 3, de voorste is 1 en de periode is 89.
Referenties
- Pedagogische bijdragen en didactisch materiaal. Decimale notatie. Hersteld van: tecdigital.TEC.AC.Cr.
- Baldor, een. 2007. Praktische theoretische rekenkunde. Redactionele groep Patria s.NAAR. van C.V.
- Wiskunde voor transacties. Decimale notatie begrijpen. Opgehaald uit: OpenTextbc.AC.
- UNAM. Rationele getallen: betekenissen en representaties. Hersteld van: Redi.Codeisch.UNAM.mx.



&space;\:&space;3.1\widehat89)