Geschiedenis van de reële getallen, voorbeelden, eigenschappen, bewerkingen

De echte getallen Ze vormen de numerieke set die natuurlijke getallen, gehele getallen, rationeel en irrationeel omvat. Ze worden aangeduid met het symbool ℝ of eenvoudigweg R En het bereik dat ze hebben in wetenschap, engineering en economie is zodanig dat bij het praten over "nummer" bijna wordt aangenomen dat het een reëel aantal is.

De reële getallen worden sinds de oudheid gebruikt, hoewel ze die naam niet kregen. Vanaf het moment dat Pythagoras zijn beroemde stelling ontwikkelde, ontstonden er getallen die niet konden worden verkregen als vrij natuurlijke getallen of hele getallen.

Figuur 1. Venn -diagram dat laat zien hoe de set reële getallen de andere numerieke sets bevat. Bron> Wikimedia Commons.

Voorbeelden van getallen zijn √2, √3 en π. Deze cijfers worden genoemd irrationeel, In tegenstelling tot rationele getallen, die afkomstig zijn van quotiënten tussen hele getallen. Het was daarom een ​​numerieke set die beide soorten cijfers omvat.

De term "reële getal" is gemaakt door de grote wiskundige René Descartes (1596-1650), om onderscheid te maken tussen de twee soorten wortels die kunnen voortvloeien uit het oplossen van een polynoomvergelijking.

Sommige van deze wortels kunnen paren van negatieve getallen zijn, deze Descartes noemden ze "denkbeeldige getallen" en degenen die dat niet waren, waren reële getallen.

De denominatie bleef in de loop van de tijd bestaan, wat leidde tot twee grote numerieke sets: reële getallen en complexe getallen, een bredere set die reële getallen omvat, denkbeeldig en degenen die in echt en gedeeltelijk denkbeeldig zijn.

De evolutie van reële getallen ging door tot in 1872, de wiskundige Richard Dedekind (1831-1936) definieerde met alle formaliteit de reële getallen door de oproepen Cortures Dedekind. De synthese van zijn werk werd gepost in een artikel dat het licht datzelfde jaar zag.

Kan u van dienst zijn: reguliere polygonen: eigenschappen, elementen, hoeken, voorbeelden

[TOC]

Voorbeelden van reële getallen

De volgende tabel toont voorbeelden van reële getallen. Deze set heeft als subset voor natuurlijke getallen, gehele getallen, rationeel en irrationeel. Een willekeurig aantal van deze sets is op zichzelf een reëel getal.

Daarom zijn de 0, de negatieven, de positieve, breuken en decimalen reële getallen.

Figuur 2. Voorbeelden van reële getallen zijn de inboorlingen, de gehele getallen, het rationele, de irrationele en de transcendenten. Bron: f. Zapata.

Weergave van reële getallen op de echte lijn 

Echte getallen kunnen op de echte lijn worden weergegeven R, Zoals de foto laat zien. Het is niet nodig dat de 0 altijd aanwezig is, maar het is handig om te weten dat de negatieve reacties links en rechts de positieve zijn. Daarom is het een uitstekend referentiepunt.

Op de echte lijn wordt een schaal genomen, waarin de gehele getallen worden gevonden:… 3, -2, -1, 1, 2, 3 .. . De pijl geeft aan dat de lijn zich uitstrekt tot oneindig. Maar dat is niet alles, in een interval beschouwd, zullen we altijd oneindige reële getallen vinden.

Echte getallen worden in volgorde weergegeven. Om te beginnen is er de volgorde van hele getallen, waarin positief.

Deze volgorde blijft binnen de reële getallen. De volgende ongelijkheden worden als een voorbeeld getoond:

a) -1/2 < √2

zijn < π

c) π> -1/2

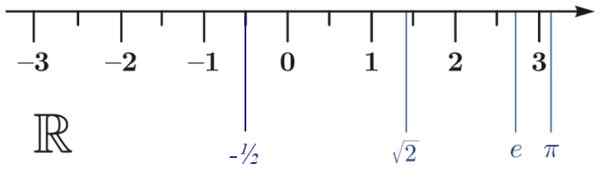figuur 3.- De echte lijn. Bron: Wikimedia Commons.

Eigenschappen van reële getallen

-Echte getallen omvatten natuurlijke getallen, gehele getallen, rationeel en irrationeel.

Kan u van dienst zijn: wat zijn driehoekige cijfers? Eigenschappen en demonstraties

-Het commutatieve eigendom van de som is vervuld: de volgorde van de addends verandert de som niet. Als A en B twee reële getallen zijn, is het altijd waar dat:

A + B = B + A

-0 is het neutrale element van de som: a + 0 = a

-De associatieve eigenschap wordt voor de som gehaald. Als a, b en c reële getallen zijn: (a + b) + c = a + (b + c).

-Het tegenovergestelde van een reëel getal a is -a.

-De aftrekking wordt gedefinieerd als de som van het tegenovergestelde: a - b = a + (-b).

-De commutatieve eigenschap van het product is vervuld: de volgorde van de factoren verandert het product niet: a.B = B.naar

-De associatieve eigenschap wordt ook op het product toegepast: (a.B).C = A.(B.C)

-De 1 is het neutrale element van vermenigvuldiging: a.1 = A

-De distributieve eigenschap van vermenigvuldiging met betrekking tot de toevoeging is geldig: a. (b+c) = a.B + A.C

-De divisie door 0 is niet gedefinieerd.

-Elk reëel getal a, behalve 0, heeft multiplicatief omgekeerd naar^-1 zodanig dat een.naar^-1 = 1.

-Als a een reëel getal is: a⁰ = 1 en a¹ = a.

-De absolute waarde of module van een reëel getal is de afstand tussen dit nummer en 0.

Bewerkingen met reële cijfers

Met de reële getallen kunt u de bewerkingen uitvoeren die zijn gemaakt met de andere numerieke sets, waaronder som, aftrekking, vermenigvuldiging, divisie, verbetering, straling, logaritmen en meer.

Zoals altijd is de verdeling met 0 niet gedefinieerd, er zijn ook geen logaritmen van negatieve getallen of 0, hoewel het waar is dat log 1 = 0 en dat logaritmen van getallen tussen 0 en 1 negatief zijn.

Toepassingen

De toepassingen van reële getallen op allerlei situaties zijn extreem gevarieerd. Echte getallen verschijnen in reactie op veel problemen in exacte wetenschappen, computer, engineering, economie en sociale wetenschappen.

Het kan je bedienen: Hipparco van Nicea: biografie en bijdragen aan de wetenschap

Alle soorten grootten en bedragen zoals afstanden, tijden, krachten, geluidsintensiteit, geld en nog veel meer, hebben hun uitdrukking in reële getallen.

De verzending van telefoonsignalen, het beeld en het geluid van een video, de temperatuur van een airconditioning, een verwarming of een koelkast kan digitaal worden geregeld, wat betekent dat de fysieke grootten worden omgezet in numerieke sequenties.

Hetzelfde gebeurt wanneer een banktransactie online wordt uitgevoerd of instant messaging wordt geraadpleegd. De reële getallen zijn overal.

Oefening opgelost

Laten we eens kijken met oefeningen hoe deze cijfers werken in gemeenschappelijke situaties waarmee we dagelijks zijn.

Oefening 1

Het postkantoor accepteert alleen pakketten waarvoor de lengte, plus de contourmeting, niet groter is dan 108 inch. Daarom moet worden vervuld om het aangetoond pakket te accepteren dat:

L + 2 (x + y) ≤ 108

a) Wilt u een pakket passeren dat 6 centimeter breed, 8 inch lang en 5 voet lang meet?

b) Hoe zit het met een die 2 x 2 x 4 voet meet³?

c) Wat is het hoogst acceptabel voor een pakket waarvan de basis vierkant is en 9 x 9 inch meet²?

Antwoord op

L = 5 voet = 60 inch

x = 6 inch

y = 8 inch

De te oplossen bewerking is:

L + 2 (x + y) = 60 + 2 (6 + 8) inch = 60 + 2 x 14 inch = 60 + 28 inch = 88 inch

Het pakket wordt geaccepteerd.

Antwoord B

De afmetingen van dit pakket zijn lager dan die van pakket A), dus beide slagen erin om te passeren.

Antwoord C

In dit pakket:

x = l = 9 inch

Het moet worden vervuld dat:

9+ 2 (9+ y) ≤ 108

27 + 2y ≤ 108

2y ≤ 81

en ≤ 40.5 inch

Referenties

1. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
2. Diego, a. Echte getallen en hun eigenschappen. Hersteld van: wiskunde.Onbelangrijk.Edu.AR.
3. Figuera, j. 20000000000000000000. Wiskunde 9e. Rang. Co-bo edities.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.